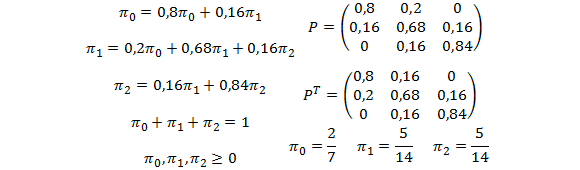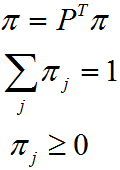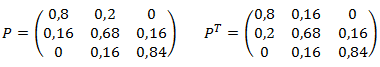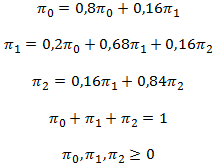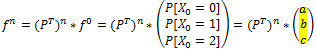Una Distribución Límite (estacionaria) de una Cadena de Markov en tiempo discreto consiste en una distribución de estado estable para los estados de una cadena que es independiente de la distribución inicial.
En distintas aplicaciones de esta categoría de procesos estocásticos resulta de interés identificar la probabilidad de que la variable aleatoria «Xn» adopte un valor «j» (entre M estados posibles) al cabo de un número de etapas o transiciones «n» que tiende a infinito. Lo anterior equivale a:
En este contexto existen ecuaciones que permiten encontrar estas probabilidades de largo plazo en la medida que el proceso markoviano en tiempo discreto sea una cadena irreducible con estados recurrentes positivos aperiódicos.
Para ello se requiere en primera instancia Clasificar los Estados de la Cadena de Markov de modo de corroborar las condiciones anteriores.
En forma compacta las ecuaciones que permiten encontrar las probabilidades estacionarias son:
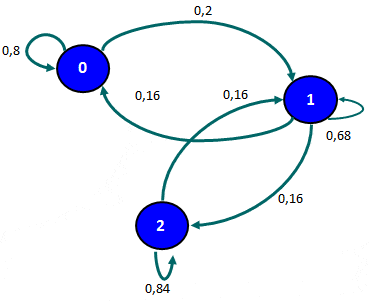
Consideremos el siguiente ejemplo que satisface las condiciones enunciadas previamente. ¿Cuál es la probabilidad de que en el largo plazo el proceso se encuentre en el estado 0, 1 o 2?.
La matriz de probabilidades de transición en una etapa (y su respectiva matriz transpuesta) son las siguientes:
El sistema de ecuaciones que permite encontrar las probabilidades de estado estable queda especificado por:
La resolución del sistema anterior permite obtener:
Es decir, la probabilidad de que en el largo plazo el proceso se encuentre en el estado 0, 1 y 2 es de un 28,57%, 35,71% y 35,71%, respectivamente (las probabilidades han sido aproximadas a dos decimales). Esto es independiente de la distribución inicial, es decir, en qué estado actualmente se encuentre la variable aleatoria.
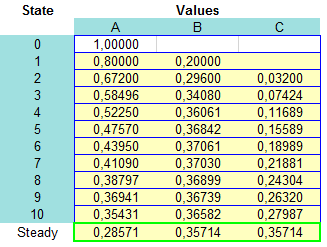
Conclusión: Se puede corroborar los resultados anteriores utilizando las fórmulas matriciales para encontrar la distribución de estado para una etapa «n». Para ello seleccionamos un valor de «n» relativamente «grande» y una distribución inicial cualquiera (se deben seleccionar valores de a, b y c mayores o iguales a cero tal que a+b+c=1). Con esto se puede verificar que independiente de la distribución inicial las probabilidades de largo plazo convergerán asintóticamente a los valores obtenidos anteriormente.
Por ejemplo, estableciendo (arbitrariamente) a=1, b=0, c=0 se logran las siguientes probabilidades de estado al cabo de 10 transiciones (con color verde se muestra las probabilidades estacionarias).