El Problema del Vendedor de Periódicos (también conocido como Newsvendor Problem) es una forma sencilla de ilustrar una categoría de problemas con demanda incierta (estocástica) pero con distribución de probabilidad conocida, donde se debe determinar el tamaño de pedido o lote económico que minimice una función de costos esperados.
Este problema es de un sólo período debido a que los periódicos que no se logran vender en un día no se pueden vender al día siguiente a un valor de mercado y por tanto cada exceso de inventario (tamaño de pedido superior a la demanda) tiene un costo monetario asociado.
Sin embargo, en algunas ocasiones se asume que si se puede vender el inventario en exceso pero a un precio que usualmente es significativamente menor que el costo de adquisición. Este sería, por ejemplo, el caso de una panadería que vende el pan que le sobra de un día al día siguiente a un precio descontado.
En el mismo contexto, realizar un pedido insuficiente para enfrentar la demanda tiene un costo de oportunidad asociado, que en el mejor de los casos se puede estimar como el margen no logrado por quiebre de stock, pero que en la práctica puede incluso provocar la pérdida del cliente (costo muy complejo de estimar).
Consideremos los siguientes parámetros del Modelo Newsvendor:
- Costo unitario c.
- Valor de consignación h (items no vendidos).
- Costo de quiebre de stock (stock-out) p (costo de imagen).
- Demanda desconocida con distribución de probabilidad conocida F(x).
La función que permite minimizar el costo esperado asociado al inventario es:
Donde la solución óptima esta dada por:
Ejemplo Problema del Vendedor de Diarios (Newsvendor Problem)
Un vendedor de periódicos elige todas las noches que cantidad de periódico él va a pedir al editor. El costo unitario es $1.5 pero él puede devolver al editor periódicos no vendidos y recibir a cambio $0.9. Cada cliente que llega a su tienda y sale sin periódico tiene un costo de $2.5 para el vendedor. Suponiendo que la demanda por periódicos es uniforme en el intervalo [50,150], ¿cuántos periódicos el vendedor debe pedir diariamente al editor?.
Primero debemos determinar cuáles son los parámetros del modelo: c=$1.5, h=$0.9, p=$2.5 y F(x)~U[50,150]. Luego evaluamos en F(y*) para obtener el tamaño de pedido que minimiza la función de costo esperado:
La cantidad de periódicos que debe pedir el vendedor es 112 unidades. Notar que si bien en el denominador de la fórmula se considera h con signo positivo, en el ejemplo dicho valor corresponde a un ingreso (lo que el vendedor puede rescatar o recuperar por cada unidad que no logra vender. Esto se conoce alternativamente como salvage value) por tanto se evalúa con signo negativo.
Finalmente al evaluar el tamaño óptimo de pedido en la función de costo esperado se obtiene:
Donde μ es la media de la variable aleatoria que representa el comportamiento de la demanda.
En el ejemplo la media de una distribución uniforme entre [50,150] es μ=(50+150)/2=100. Finalmente al desarrollar la expresión se obtiene C(112)=$168,752.
Te recomendamos evaluar otro tamaño de pedido (por ejemplo y=100 o y=140) en la función de costos esperado y verificar que el costo que se alcanza es mayor a C(112)=$168,752.
Finalmente: ¿Cuál es la probabilidad de satisfacer la demanda para el vendedor de periódicos en un día cualquiera?.
Si compra y=112 periódicos la probabilidad de Instock es P[D<=112]=(112-50)/(150-50)=62%. Esto implica que la probabilidad de incurrir en un quiebre de stock para el tamaño de pedido que minimiza la función de costos esperados es de un 38% (100%-62%).
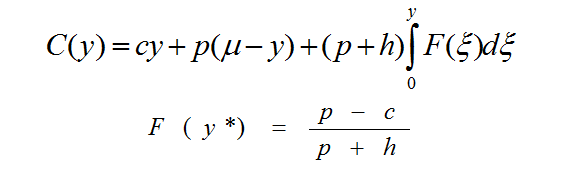
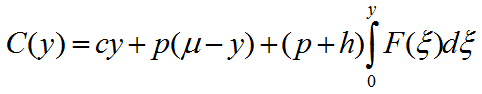
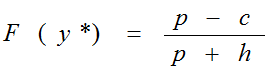
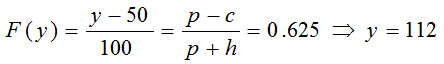
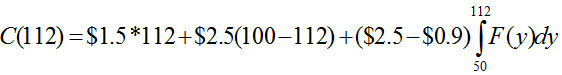
Bien explicado. ¿Cuál sería la ventaja y desventaja del modelo?. Gracias.
Como pasan de F(y)= a 0.625 a esas 112 unidades?. Gracias de antemano, no comprendo los cálculos que colocaron.
@Walter, se obtiene al despejar y de la ecuación (y-50)/100=0,625. Se obtiene y=112[u] (aproximado).
Hola, una consulta: ¿qué pasa si el vendedor debe tomar dos decisiones, cuánto vender en la mañana y si deberá pedir o no más diarios para la tarde?, en este caso puedo aplicar este ejemplo para definir cuánto pedir en la mañana, pero para la tarde ¿cómo podría hacerlo?
Muy útil y bien explicado! muchas gracias