Gestión de Operaciones

Tratamiento de Puntos Atípicos en Series de Tiempo con R Software

Los puntos atípicos (también denominados puntos aberrantes o outliers) siempre son un problema al momento de querer ajustar una serie de tiempo, o querer hacer predicciones para valores futuros. Recordamos al lector que una serie de tiempo se define como un conjunto de valores observados en un horizonte de tiempo y cumplen con ser equidistantes (por lo tanto, pueden ser observaciones tomadas por días, meses, trimestres, años, etc.).

Además, otra observación importante es que la decisión a tomar con respecto a qué se debe hacer con dichos valores es una elección que considera aspectos cuantitativos como cualitativos, ya que si bien se pueden utilizar test para decidir qué hacer con el punto, la decisión final siempre dependerá del modelador: pueden haber aspectos importantes en los datos que un test estadístico no es capaz de evaluar, y si el modelador cree que el punto debe estar por que representa un aspecto de la realidad, entonces se deberán asumir las consecuencias que implica dejar un punto que cuantitativamente puede ser considerado atípico.

En este artículo presentamos una forma de tratar puntos atípicos en una serie de tiempo. Los datos presentados se ordenan mensualmente en un horizonte de 8 años, y se utilizará R software (un programa freeware) para identificar y eliminar dichos puntos.

Siempre lo primero que debemos realizar al tener un conjunto de datos, es graficarlos para ver a priori su comportamiento. Este ejemplo utiliza una librería llamada “tseries”. Para descargarla, se debe seguir la siguiente instrucción: En el menú superior ir a la pestaña Paquetes:

Paquetes ==> Instalar Paquete(s)… ==> Seleccionar servidor ==> tseries

La siguiente porción de código permite cargar los datos, transformarlos en una serie y luego graficarlos.

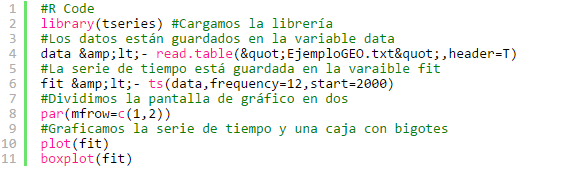
#R Code
library(tseries) #Cargamos la librería
#Los datos están guardados en la variable data
data &lt;- read.table("EjemploGEO.txt",header=T) 
#La serie de tiempo está guardada en la varaible fit
fit &lt;- ts(data,frequency=12,start=2000)
#Dividimos la pantalla de gráfico en dos
par(mfrow=c(1,2))
#Graficamos la serie de tiempo y una caja con bigotes
plot(fit)
boxplot(fit)

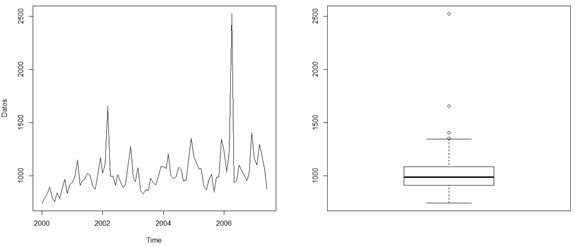
El resultado se puede apreciar en la siguiente imagen:

Como se puede ver, gráficamente podemos identificar dos puntos aberrantes, cerca del año 2002 y 2006. Además, un análisis mediante la caja con bigotes nos muestra cuatro puntos aberrantes. Este diagrama puede ser un poco más estricto, por lo tanto acá es importante destacar que es decisión del modelador sacar los cuatro, sólo dos (los de mayor impacto que se ven en el gráfico de la izquierda) o ninguno.

Para este ejemplo, consideraremos que vamos a sacar sólo los puntos que generan un mayor impacto en la serie, y son los que se pueden ver en el gráfico de la izquierda.

El análisis gráfico nos ayuda pero nunca es concluyente. Por lo anterior debemos utilizar siempre métodos cuantitativos para identificar los puntos (recordando nuevamente que la decisión sobre qué hacer con ellos depende tanto de factores cuantitativos como cualitativos).

Para poder identificar puntos outliers en la serie de tiempo, ocuparemos la librería “tsoutliers” la cual se puede descargar de la misma forma enseñada anteriormente.

#R Code
library(tsoutliers) #Cargamos la librería
#El comando tso identifica los puntos atípicos de la serie
outliers <- tso(fit) 
#Graficamos la nueva serie
plot(outliers)

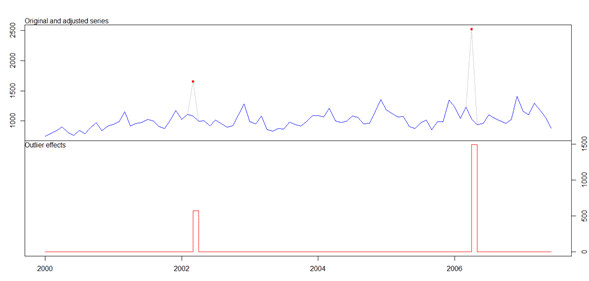
El resultado se muestra a continuación:

Podemos ver que esta función logra identificar (y pone en rojo) los puntos que considera aberrantes en la serie, y no sólo hace eso, sino que gráfica una serie “ajustada” (en azul), calculando un nuevo valor para dichos puntos en base a la información de los otros puntos pertenecientes a los datos.

¿Qué hacer con los puntos aberrantes?: Podemos sacarlos, modificarlos o dejarlos como están. Si los sacamos perdemos información; pero si los dejamos como están afectarán en la predicción de los valores futuros.

Una primera aproximación en estos casos siempre es calcular un promedio de los valores que están cerca del punto donde se produce el dato atípico, además, los estadísticos han desarrollado métodos más sofisticados para tratar con ellos, y dejamos este estudio al lector.

Como mencionamos anteriormente, esta función genera un valor que se ajusta de acuerdo al comportamiento de los datos (como se puede ver en el gráfico azul), por lo que utilizaremos dichos valores para ajustar una nueva serie, la cual tendrá los puntos aberrantes corregidos (dejamos también al estudio del lector la forma en que esta función modifica los datos, lo cual se puede encontrar en la documentación de la función disponible vía web).

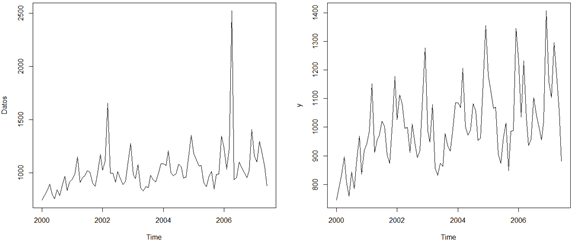
#R Code
#Obtenemos los valores modificados
newserie <- outliers$yadj 
#Dividimos la pantalla de gráficos en 2
par(mfrow=c(1,2))
#Graficamos la serie antigua y la nueva
plot(fit)
plot(newserie)

Podemos ver la nueva forma que tiene la serie, al tener valores modificados para los puntos atípicos (cuidado: la serie ha cambiado su forma drásticamente debido a los puntos aberrantes, pero el efecto se incrementa ya que ha cambiado la escala a la que se muestran ambos gráficos, notar que en el de la izquierda llega hasta 2.500 y ahora sólo hasta 1.400).

Como hemos podido ver, este simple método nos ha permitido hacer un tratamiento sobre los puntos atípicos identificados en la serie de datos. Como hemos mencionado reiteradamente, existen varios métodos para poder hacer esto, y la decisión final siempre tendrá una parte subjetiva que depende del modelador, ya que los criterios pueden variar, y puede ser que el origen de los datos justifique (y permita) la existencia de los puntos aberrantes. Para concluir, con la modificación realizada ahora si podemos pensar en predecir los valores futuros de la serie.

Método de Descomposición de Benders

La Descomposición de Benders es, como su nombre lo dice, un Método de Descomposición. La idea de este método es bastante simple: dividir para conquistar. El objetivo es literalmente descomponer el problema en dos partes: El Master Problem (Problema Maestro) y el Subproblem (Subproblema) (también llamado Slave Problem o Problema Esclavo). En el siguiente artículo revisaremos de qué se trata el Método de Descomposición de Benders, en conjunto con la presentación de su uso en un pequeño ejemplo.

Esta metodología fue propuesta por J.F. Benders en 1962, su nombre original es Partitioning procedures for solving mixed-variables programming problems, y como su nombre bien lo dice el método está pensado originalmente para problemas de Programación Entera Mixta. Sin embargo, también se puede aplicar en problemas de Programación Lineal.

El Método de Descomposición de Benders trabaja bajo el concepto de las “variables complicadas”, es decir las variables que hacen que nuestro problema se «complique». Si estas variables no existieran (o más bien, conociéramos su valor de forma anticipada) entonces el problema resultante se supone que es considerablemente más fácil de resolver.

En Programación Entera Mixta, se espera que estas variables “complicadas” sean las enteras, las cuales al fijar su valor, dejan un problema resultante que cumple con una característica muy conveniente: es lineal. Y como cumple con esto, entonces podemos hacer uso de todo lo que conocemos sobre Programación Lineal para realizar la optimización de las variables que (en un principio) fijamos.

Veamos entonces brevemente de que se trata el Método de Descomposición de Benders. Supongamos que tenemos un problema que tiene la siguiente estructura:

Como mencionamos al principio, entonces podemos separar este problema en dos partes. A continuación se muestra el Master Problem (Problema Maestro) a la izquierda y el Subproblem (Subproblema) a la derecha:

Como se puede ver, el Master Problem contiene las variables que son enteras, y el Subproblem contiene las variables continuas, por lo que este último cumple con ser un problema de Programación Lineal.

Notar que el lado derecho de las restricciones del problema esclavo son números, ya que los valores de las variables enteras están fijos.

Iniciamos este artículo diciendo que el concepto central es dividir para conquistar: en este caso lo que se hace es resolver el Problema Maestro para obtener los valores de y; con esto, podemos resolver entonces el Subproblema. Se puede observar que el valor de la función objetivo del Subproblema se encuentra en la función objetivo del Problema Maestro, lo anterior se reformulará más adelante.

Una nota relevante: Si te das cuenta, el Problema Maestro para esta formulación no tiene ninguna restricción más que las de dominio. Nada impide que el Problema Maestro también tenga restricciones. Esto estará dado por la estructura del problema que estemos estudiando.

Recuerda siempre: ambos problemas están conectados, por lo que el resultado de uno influye directamente en el resultado del otro. Con esto en consideración, se cumple la siguiente propiedad:

Si el Subproblema es no acotado, entonces el Problema Maestro también lo es, resultando en que el problema original es no acotado.

Si tenemos un problema de Programación Lineal, entonces tenemos que aprovecharlo. ¿Qué es lo primero que se nos viene a la mente con un problema lineal? La respuesta es dualidad. Cada problema lineal (primal) tiene su problema dual asociado, el cual para el caso del problema esclavo enunciado anteriormente, tiene la siguiente estructura:

¿Qué es lo que podemos ver en este problema dual?: Que la región factible (es decir el sub-espacio definido por las restricciones y el dominio del problema) no depende del valor que tomen las variables enteras, y sólo influye en el valor de la función objetivo (notar que están en ella).

Lo anterior entonces nos lleva a la siguiente pregunta: ¿Qué sucede cuando la región factible del problema es vacía? (recuerda que al ser vacía estamos diciendo que nuestro problema dual es infactible). Dos cosas pueden ocurrir:

Al ser el problema dual infactible, entonces su primal es no acotado para algún valor de las variables enteras, en cuyo caso el problema original también es no acotado, o bien
La región factible del problema primal es también infactible para todo valor de las variables enteras, llevando a la conclusión de que el problema original es infactible.

¿Por qué revisamos todo esto?: Porque es importante tenerlo en consideración, ya que como mencionamos anteriormente, al tener un problema esclavo lineal, entonces podemos hacer el uso de los conceptos de dualidad.

¿Para qué la usaremos?: Para reformular nuestro Problema Maestro, y transformarlo en lo que usualmente se conoce como Relaxed Master Problem (RMP). Esta reformulación utiliza las variables duales asociadas a las restricciones del Slave Problem primal.

El Relaxed Master Problem (Problema Maestro Relajado) se puede escribir de la siguiente forma:

A las restricciones (1) y (2) se les conoce como restricciones de factibilidad y optimalidad, respectivamente. Además, existe una variable auxiliar z, la cual permite es la responsable de hacer la “conexión” entre el Problema Maestro y el Subproblema (esto se puede ver en las restricciones del tipo (1) y (2)).

Al resolver el RMP vamos a obtener los valores de las variables enteras, las cuales utilizaremos para resolver el Subproblema, como resultado podemos obtener dos cosas:

El sub-problema es infactible, lo cual implica que el problema dual es no acotado. Si esto ocurre, debemos agregar un corte de factibilidad al RMP.
El sub-problema tiene una solución óptima, lo cual implica que el problema dual también la tiene. Si esto ocurre, entonces hay que agregar un corte de optimalidad al RMP.

La última pregunta que nos queda por responder es: ¿Cuántas veces iterar?. Para responder lo anterior debemos definir la cota superior e inferior.

La cota superior corresponde al valor de la función objetivo original de nuestro problema; la cota inferior corresponde a la función objetivo del Master Problem, por lo tanto, debemos continuar hasta que ambos valores sean iguales.

Como la teoría de esta descomposición puede ser un poco compleja, veamos un ejemplo.

Ejemplo Método de Descomposición de Benders (Programación Lineal)

El ejemplo que veremos a continuación corresponde a un problema de Programación Lineal. La aplicación es similar para los problemas de Programación Entera Mixta.

Supongamos que tenemos que resolver el siguiente problema:

La solución óptima para este problema es: $x_{1}=0$ , $x_{2}=0,714$ e $y=1,571$ con un valor para la función objetivo (valor óptimo) de 5,285. La solución óptima del problema anterior se puede alcanzar de forma sencilla a través del Método Simplex Dual o el Método Simplex de 2 Fases (y por cierto a través de otros procedimientos y herramientas computacionales como Solver de Excel).

Vamos a descomponer el problema de la siguiente forma: recuerda que utilizaremos el RMP (Problema Maestro Relajado). Sea esta la primera iteración, K=1.

Al resolver el RMP de la primera iteración, obtenemos como solución óptima $y=0$ y $z=0$ ; lo cual utilizaremos para resolver el Subproblema. Con $y=0$ , el resultado del Subproblema es: $x_{1}=2,2$ y $x_{2}=0,4$ con un valor en la función objetivo de 5,6.

Ahora debemos calcular la cota superior (UB) y cota inferior (LB):

Como difieren el valor de las cotas, debemos continuar. Gracias a la herramienta “Análisis de Sensibilidad” del Solver en Excel, podemos obtener el valor de las variables duales asociadas a las restricciones del Subproblema (también podríamos obtener el valor de las variables duales óptimas al utilizar el Teorema de Holguras Complementarias). Esos valores son: $\lambda_{1}=-1,6$ y $\lambda_{2}=-0,2$ .

Estos valores nos permiten crear el siguiente corte de optimalidad: $-1,6(-3+y)-0,2(-4+3y)\leq z$ , el cual agregamos al Problema Maestro:

Hacemos K=2 (contador de iteraciones) y resolvemos el Problema Maestro nuevamente. Este corte nos permite encontrar una nueva solución óptima: $y=2,545$ y $z=0$ . Con este valor de y, el resultado del Subproblema es: $x_{1}=0$ y $x_{2}=0,227$ con un valor en la función objetivo de 0,68.

Ahora debemos calcular la cota superior (UB) y cota inferior (LB):

Al ver las variables duales para las restricciones del Subproblema tenemos que: $\lambda_{1}=-1,5$ y $\lambda_{2}=0$ , lo cual permite crear el siguiente corte de optimalidad el cual agregamos al Problema Maestro:

Hacemos K=3 y resolvemos el Problema Maestro nuevamente. La nueva solución óptima para el Problema Maestro es $y=1,571$ y $z=2,142$ con un valor óptimo de 5,285. Con $y=1,571$ la solución del Subproblema es: $x_{1}=0$ y $x_{2}=0,714$ con un valor en la función objetivo de 2,148.

Ahora debemos calcular la cota superior e inferior:

Como ambas cotas (superior e inferior) son iguales, podemos detenernos. Hemos encontrado la solución óptima para nuestro problema de Programación Lineal. (Mis sinceros agradecimientos a mi amigo Javier Maturana Ross por su contribución con este detallado tutorial y los créditos correspondientes al profesor Yuping Huang por el ejemplo presentado en este artículo).

Ejemplo del Método Simplex (Tutorial y Cómo Funciona)

En el siguiente artículo detallaremos cómo funciona el Método Simplex a través de un ejemplo sencillo correspondiente a un modelo de Programación Lineal que considera 3 variables de decisión.

El Método Simplex corresponde a un algoritmo iterativo publicado por George Bernard Dantzig en el año 1947 en donde se busca alcanzar el máximo (o mínimo) de una función lineal compuesta por un conjunto de variables que deben satisfacer condiciones impuestas por restricciones lineales en forma de inecuaciones.

En este contexto, el objetivo de este artículo es definir en detalle distintas aproximaciones para la resolución de un modelo de Programación Lineal utilizando el Método Simplex, además de discutir sobre sus principales características.

Con tal propósito en perspectiva consideremos el siguiente modelo de optimización lineal:

Ejemplo del Método Simplex (Utilizando Diccionarios)

Un paso preliminar consiste en incorporar las denominadas variables de holgura. De modo de comprender este concepto consideremos la primera restricción:

$2x_{1}+3x_{2}+x_{3}\leq 5$

Para cada solución factible $x_{1},x_{2},x_{3}$ , el valor del lado izquierdo será a lo más el valor del lado derecho; o eventualmente existirá una diferencia (holgura) entre estos 2 valores.

De esta forma definimos $x_{4}$ como variable de holgura de dicha restricción, la cual se puede denotar por $x_{4}=5-2x_{1}-3x_{2}-x_{3}$ , donde $x_{4}\geq 0$ . De forma análoga se pueden definir las variables de holgura (no negativas) $x_{5}$ y $x_{6}$ para las restricciones 2 y 3, respectivamente. Finalmente podemos describir la función objetivo $5x_{1}+4x_{2}+3x_{3}$ utilizando $z$ de forma compacta.

En resumen, para cada selección de valores de las variables $x_{1},x_{2}$ y $x_{3}$ podemos definir valores para las variables $x_{4},x_{5},x_{6}$ , y $z$ utilizando las siguientes fórmulas (conocido comúnmente como diccionarios según la terminología utilizada en el libro Linear Programming de Vasek Chvátal):

$x_{4}=5-2x_{1}-3x_{2}-x_{3}$
$x_{5}=11-4x_{1}-x_{2}-2x_{3}$
$x_{6}=8-3x_{1}-4x_{2}-2x_{3}$
$z=5x_{1}+4x_{2}+3x_{3}$

El objetivo del Método Simplex es lograr sucesivas mejoras para el valor de la función objetivo asociada a la selección de alguna solución factible. Repetir dicho procedimiento un numero finito de veces debería permitir eventualmente alcanzar la solución óptima del problema lineal en estudio.

Para inicializar el Método Simplex necesitamos una solución factible. En nuestro ejemplo esto es sencillo y se puede alcanzar simplemente fijando las variables $x_{1},x_{2},x_{3}$ en cero. De esta forma se alcanzan los siguientes resultados:

$x_{1}=0,x_{2}=0,x_{3}=0,x_{4}=5,x_{5}=11,x_{6}=8,z=0$

En el contexto del objetivo planteado anteriormente, debemos buscar una solución factible que permita alcanzar un mayor valor para $z$ . Si, por ejemplo, mantenemos $x_{2}=x_{3}=0$ e incrementamos el valor de $x_{1}$ obtenemos $z=5x_{1}>0$ , de modo que si $x_{1}=1$ se obtiene $z=5$ (y $x_{4}=3,x_{5}=7,x_{6}=5$ ). Mejor aún, si $x_{1}=2$ (manteniendo $x_{2}=x_{3}=0$ ), se obtiene $z=10$ (y $x_{4}=1,x_{5}=3,x_{6}=2$ ).

Sin embargo, si asumimos $x_{1}=3$ (conservando $x_{2}=x_{3}=0$ ) el valor de la función objetivo ahora es $z=15$ , pero $x_{4}=-1,x_{5}=-1,x_{6}=-1$ que claramente no satisface las condiciones de no negatividad para las variables.

Por tanto la pregunta relevante es: ¿cuánto se puede incrementar el valor de $x_{1}$ (manteniendo $x_{2}=x_{3}=0$ al mismo tiempo) y seguir conservando la factibilidad ( $x_{4},x_{5},x_{6}\geq 0$ )?.

La condición $x_{4}=5-2x_{1}-3x_{2}-x_{3}\geq 0$ implica $x_{1}\leq \frac{5}{2}$ ; de forma similar $x_{5}\geq 0$ implica $x_{1}\leq \frac{11}{4}$ y $x_{6}\geq 0$ implica $x_{1}\leq \frac{8}{3}$ . Claramente de estas 3 cotas para la variable $x_{1}$ la más restrictiva es $x_{1}\leq \frac{5}{2}$ , de modo que incrementamos el valor de $x_{1}$ hasta ese valor de modo de obtener una nueva solución:

$x_{1}=\frac{5}{2},x_{2}=0,x_{3}=0,x_{4}=0,x_{5}=1,x_{6}=1/2,z=\frac{25}{2}$

Que claramente constituye una mejora para el valor de la función objetivo en comparación al valor inicial $z=0$ .

A continuación debemos buscar una nueva solución factible que sea aún mejor que la que acabamos de encontrar. Para ello la variable $x_{1}$ que cambió su valor desde cero a un número positivo (12,5), debe cambiar su lugar desde el lado derecho al lado izquierdo del sistema de ecuaciones. De forma análoga, la variable $x_{4}$ que cambio su valor de un número positivo a cero debe cambiar de lugar desde el lado derecho al lado izquierdo.

De esta forma y luego de cierta manipulación algebraica podemos reescribir $x_{1}$ en términos de $x_{2},x_{3},x_{4}$ según se observa a continuación:

$x_{1}=\frac{5}{2}-\frac{3}{2}x_{2}-\frac{1}{2}x_{3}-\frac{1}{2}x_{4}$

Luego, con el objetivo de expresar $x_{5},x_{6}$ y $z$ en términos de $x_{2},x_{3},x_{4}$ , simplemente substituimos el resultado anterior en las filas correspondientes:

$x_{5}=11-4(\frac{5}{2}-\frac{3}{2}x_{2}-\frac{1}{2}x_{3}-\frac{1}{2}x_{4})-x_{2}-2x_{3}$
$x_{5}=1+5x_{2}+2x_{4}$

$x_{6}=8-3(\frac{5}{2}-\frac{3}{2}x_{2}-\frac{1}{2}x_{3}-\frac{1}{2}x_{4})-4x_{2}-2x_{3}$
$x_{6}=\frac{1}{2}+\frac{1}{2}x_{2}-\frac{1}{2}x_{3}+\frac{3}{2}x_{4}$

$z=5(\frac{5}{2}-\frac{3}{2}x_{2}-\frac{1}{2}x_{3}-\frac{1}{2}x_{4})+4x_{2}+3x_{3}$
$z=\frac{25}{2}-\frac{7}{2}x_{2}+\frac{1}{2}x_{3}-\frac{5}{2}x_{4}$

De esta forma nuestro sistema de ecuaciones (diccionario) queda definido por:

$x_{1}=\frac{5}{2}-\frac{3}{2}x_{2}-\frac{1}{2}x_{3}-\frac{1}{2}x_{4}$
$x_{5}=1+5x_{2}+2x_{4}$
$x_{6}=\frac{1}{2}+\frac{1}{2}x_{2}-\frac{1}{2}x_{3}+\frac{3}{2}x_{4}$
$z=\frac{25}{2}-\frac{7}{2}x_{2}+\frac{1}{2}x_{3}-\frac{5}{2}x_{4}$

Como lo hicimos en la primera iteración debemos intentar incrementar el valor de la función objetivo ( $z$ ) seleccionando una variable adecuada en el lado derecho, mientras que al mismo tiempo mantenemos las restantes variables del lado derecho en cero. En este sentido se puede observar que aumentar el valor de las variables $x_{2}$ o $x_{4}$ generaría una disminución en el valor de $z$ que va en sentido contrario a nuestro objetivo de maximizar el valor de la función objetivo.

Por tanto, la única selección de una variable en el lado derecho que permitirá aumentar el valor de $z$ es seleccionar la variable $x_{3}$ .

¿Cuánto debemos incrementar el valor de $x_{3}$ ?. La respuesta se puede obtener directamente del sistema de ecuaciones anterior, considerando $x_{2}=x_{4}=0$ , la restricción $x_{1}\geq 0$ implica que $x_{3}\leq 5$ ; la restricción $x_{5}\geq 0$ no impone condiciones adicionales y la restricción $x_{6}\geq 0$ implica $x_{3}\leq 1$ . En consecuencia $x_{3}=1$ es el mejor valor que puede adoptar dicha variable.

La nueva solución corresponde a:

$x_{1}=2,x_{2}=0,x_{3}=1,x_{4}=0,x_{5}=1,x_{6}=0,z=13$

El valor de $z$ paso de 12,5 a 13 al cabo de una iteración del Método Simplex.

A continuación actualizamos el sistema de ecuaciones donde las variables que adoptan valores positivos $x_{1},x_{3},x_{5}$ se encontraran en el lado izquierdo, mientras las variables igual a cero estarán en el lado derecho. De este modo pasamos la variable $x_{3}$ al lado izquierdo, donde $x_{3}=1+x_{2}+3x_{4}-2x_{6}$ que permite substituir en el resto de las ecuaciones:

$x_{3}=1+x_{2}+3x_{4}-2x_{6}$
$x_{1}=2-2x_{2}-2x_{4}+x_{6}$
$x_{5}=1+5x_{2}+2x_{4}$
$z=13-3x_{2}-x_{4}-x_{6}$

Notar que no es posible seguir aumentando el valor de la función objetivo $z$ mediante un incremento de las variables del lado derecho $x_{2},x_{4},x_{6}$ (en efecto, el valor de $z$ decrecería). En consecuencia estamos en presencia de la solución óptima del problema: $x_{1}=2,x_{2}=0,x_{3}=1,x_{4}=0,x_{5}=1,x_{6}=0$ con valor óptimo $z=13$ .

El procedimiento anterior basado en diccionarios favorece una mejor comprensión conceptual de los fundamentos sobre los que se basa el Método Simplex. De forma complementaria a continuación presentaremos a modo de contraste las iteraciones del Método Simplex utilizando tablas (o tableau) que comúnmente corresponde a la forma en la cual se presenta el algoritmo en cursos de pregrado.

Ejemplo del Método Simplex (Utilizando Tableau)

Consideremos nuevamente nuestro problema de Programación Lineal:

A continuación incorporamos las variables de holgura (no negativas) $x_{4},x_{5},x_{6}$ que por definición tienen coeficiente nulo (cero) en la función objetivo. De esta forma obtenemos la forma estándar (*):

(*). Para nuestros efectos consideraremos que la forma estándar de un modelo de Programación Lineal esta dada por $Minimizar[c^{t}x, Ax=b,x\geq 0]$ , siendo este formato el que preferentemente hemos utilizado para desarrollar las iteraciones del Método Simplex en otros artículos relacionados en nuestro sitio. En consecuencia la selección de dicho formato es meramente convencional.

Retomando nuestro ejemplo, el tableau inicial queda definido por:

Las variables de holgura definen una Solución Básica Factible Inicial, con $x_{4}=5,x_{5}=11,x_{6}=8$ (las variables no básicas inicialmente corresponden a las variables originales del modelo, es decir, $x_{1},x_{2},x_{3}$ que por definición adoptan un valor igual a cero.

¿Cómo verificar que el tableau inicial representa una solución básica factible óptima para el problema?.

Criterio de Optimalidad: Si en una iteración del Método Simplex se dispone de una solución básica factible y adicionalmente todos los costos reducidos son mayores o iguales que cero, parar ya que la actual solución básica factible es óptima.

En el ejemplo propuesto si bien nos encontramos frente a una solución básica factible el costo reducido de las variables no básicas son negativos, por tanto no se cumple el criterio de optimalidad, es decir, se puede seguir mejorando el valor de la función objetivo.

En este sentido consideraremos arbitrariamente $x_{1}$ como la variable que ingresa a la base, aun cuando no hay certeza que la selección de la variable no básica con el costo reducido más negativo contribuya necesariamente a la Rapidez de Convergencia del Método Simplex.

La variable que deja la base para dar lugar a $x_{1}$ se obtiene del criterio de factibilidad:

Criterio de Factibilidad: Para decidir que variable básica deja la base, es necesario calcular el mayor valor que puede tomar la variable no básica que entra a la base que garantice la factibilidad de la nueva solución básica. Para ello se considera un cuociente entre el valor de la solución básica factible actual y los coeficientes mayores a cero en la columna de la variable entrante. Si todos los cuocientes son negativos el Problema es No Acotado y por tanto no existe solución óptima.

En el ejemplo el criterio de factibilidad para la presente iteración esta dado por:

$Min[\frac{5}{2},\frac{11}{4},\frac{8}{3}]=\frac{5}{2}$

El menor cuociente se alcanza en la primera fila (restricción) que determina la variable que debe abandonar la base, en este caso, la variable $x_{4}$ . Luego se actualiza la tabla realizando operaciones filas considerando el denominador del mínimo cuociente como pivote. El objetivo es alcanzar en la columna de la variable $x_{1}$ lo que actualmente disponemos en la columna de la variable $x_{4}$ .

Por ejemplo, podemos dividir la fila 1 por 2 de modo de obtener un 1 en la posición del pivote. Luego sobre esta nueva fila 1 podemos multiplicarla por -4 y sumarla a la fila 2. También se puede alcanzar un cero para la variable $x_{1}$ en la fila 3 multiplicando por -3 la nueva fila 1 y sumándola a la fila 3. Finalmente para lograr un cero en el costo reducido de $x_{1}$ se multiplica por 5 la nueva fila 1 y se suma a la fila 4.

De este modo el tableau del Método Simplex al cabo de una iteración queda de la siguiente forma:

La solución básica factible actual corresponde a: $x_{1}=\frac{5}{2},x_{2}=0,x_{3}=0,x_{4}=0,x_{5}=1,x_{6}=1/2$ con valor en la función objetivo $z=\frac{25}{2}$ . Se puede apreciar que dicho resultado es consistente con el enfoque de diccionarios utilizado inicialmente.

Claramente no se satisface el criterio de optimalidad dado que la variable no básica $x_{3}$ tiene costo reducido negativo. Por ello $x_{3}$ ingresa a la base y por tanto debemos calcular nuevamente el criterio de factibilidad para determinar la variable que deberá dejar la base:

$Min[\frac{5/2}{1/2},\frac{1/2}{1/2}]=1$

El pivote ahora se encuentra en la fila 3 y en consecuencia la variable básica $x_{6}$ debe dejar la base. Notar que no se ha considerado para el cálculo del criterio de factibilidad el coeficiente de la variable $x_{3}$ correspondiente a la fila 2 del tableau anterior (cuyo valor es cero y por tanto el cuociente se indefine).

Actualizamos el tableau del Método Simplex obteniendo los siguientes resultados:

Los valores que adoptan las variables básicas correspondientes a esta nueva iteración es $x_{1}=2,x_{2}=0,x_{3}=1,x_{4}=0,x_{5}=1,x_{6}=0$ que además representa la solución óptima del modelo de Programación Lineal (dado el cumplimiento del criterio de optimalidad). Luego el valor óptimo corresponde a $z=13$ .

Importante: Existen herramientas computacionales y aplicaciones que permiten resolver online un problema de Programación Lineal mediante el Método Simplex. A continuación se presenta un extracto de los resultados alcanzados para nuestro ejemplo utilizando la aplicación disponible en http://www.programacionlineal.net/simplex.html.

Método Simplex (Conclusiones)

El ejemplo que hemos desarrollado en este artículo busca presentar de forma sencilla y didáctica los principales fundamentos asociados al Método Simplex. Cabe destacar que ha sido necesario para la aplicación del algoritmo llevar el modelo original a su forma estándar que como se discutió anteriormente puede tener distintas representaciones según la bibliografía que se consulte.

En este contexto, cada problema de Programación Lineal en su forma estándar cumple con las siguientes propiedades establecidas en el Teorema Fundamental de la Programación Lineal:

Si el problema no tiene solución óptima entonces es no-acotado o infactible.
Si tiene una solución factible, tiene una solución básica factible.
Si el problema tiene solución óptima, tiene una solución básica factible óptima.

Cabe destacar que no siempre se dispone de una solución básica factible en las variables originales del modelo (luego de llevar el problema a su forma estándar). Si bien existen diversas estrategias algorítmicas para enfrentar esta dificultad, se propone al lector revisar los tutoriales que hemos desarrollado sobre esta problemática, en particular respecto al Método Simplex de 2 Fases, Método de la M Grande y Método Simplex Dual.

Adicionalmente con el objetivo de resumir algunas ideas principales del algoritmo hemos preparado una infografía que hemos llamado 10 Cosas que Necesitas saber sobre el Método Simplex.

Finalmente quisiéramos recordar a nuestros usuarios que en el Blog de Gestión de Operaciones se pueden encontrar a la fecha más de 80 publicaciones relativas a la Programación Lineal y la Investigación de Operaciones. De modo de favorecer una rápida búsqueda ingresa al menú Cómo Comenzar. Por último agradeceríamos compartir y difundir este material en la medida que haya sido considerado útil y evaluar este tutorial utilizando las estrellas al final de esta publicación.

Ejemplo del Algoritmo de Wagner y Whitin (Sistemas de Loteo)

El Algoritmo de Wagner y Whitin (1958) consiste en una extensión natural y dinámica al problema de Tamaño Económico de Pedido (conocido también como Cantidad Económica de Pedido o EOQ) donde la demanda durante el período de planificación presenta variabilidad, no obstante, se sigue manteniendo el supuesto de asumir que dicha demanda es conocida.

De esta forma, dada una demanda que presenta variabilidad en el tiempo, costos de emisión de pedidos asociados a la gestión de los mismos y no al volumen involucrado en ellos, y costos de almacenamiento correspondientes al inventario de los productos almacenados en inventario, se busca determinar una política de pedidos que satisfaga los requerimientos de demanda al menor costo posible.

En este contexto asumiremos que el lead time (tiempo de reposición) es nulo, es decir, el pedido se recibe en el mismo período en el que se realiza y que adicionalmente estamos frente a un Problema de Tamaño de Lote No Capacitado, vale decir, que no existe limitantes de capacidad y que, eventualmente, se podría satisfacer la demanda íntegra del horizonte de planificación a través de un único pedido que se realice en el primer período (mediante la acumulación de inventarios para períodos futuros).

Un problema similar al que se aborda con el Algoritmo de Wagner y Whitin es el Problema de Producción e Inventario, en el cual frecuentemente se incorporan limitantes de capacidad para la cantidad de unidades que se pueden pedir en cada período, constituyendo de esta forma un problema capacitado.

Algoritmo de Wagner-Whitin

Los pasos detallados para la implementación del Algoritmo de Wagner y Whitin pueden encontrarse en la publicación académica original: Dynamic Version of the Economic Lot Size Model, (Versión Dinámica del Tamaño Económico de Pedido) disponible para descarga por un valor de 30 dólares. No obstante, a continuación resumiremos los pasos del algoritmo y presentaremos un ejemplo de su aplicación para favorecer su comprensión.

Paso 1: Considere la política de ordenar en el período $t^{**}$ , $t^{**}=1,2,$ …, $t^{*}$ y satisfacer las demandas $d_{t}$ , $t=t^{**},t^{**}+1,$ …, $t^{*}$ en ese orden.
Paso 2: Determine el costo total de las $t^{*}$ políticas de pedido, sumando los costos de emisión y almacenamiento asociados a la emisión de un pedido en $t^{**}$ , y el costo de actuar de forma óptima entre el período 1 y el período $t^{**}-1$ consideradas por si mismas.
Paso 3: De las $t^{*}$ alternativas, seleccione la política de mínimo costo del período 1 hasta $t^{*}$ consideradas de forma independiente.
Paso 4: Continué al período $t^{*}+1$ o detengase si $t^{*}=N$ donde $N$ representa el horizonte de planificación.

Ejemplo del Algoritmo de Wagner y Whitin

Consideremos las necesidades asociadas a un producto cualquiera para un período de planificación de 12 meses (N=12). La demanda Dt que se enfrenta cada mes es variable, como así también los costos de emitir un pedido (St), no obstante, el costo unitario de almacenar una unidad en inventario de un mes a otro (Ht) por simplicidad se asumirá que es fijo.

Aplicamos a continuación el Algoritmo de Wagner y Whitin:

El plan óptimo para el período 1 es ordenar (asumiendo un costo de emisión de $85).

Para el período 2 se deben evaluar 2 posibilidades:

ordenar en el período 2 y usar la mejor política para el período 1 considerado por si solo (con un costo de emisión de $102+$85=$187).
o emitir un pedido en el período 1 para ambos períodos (1 y 2), almacenando inventario para el período 2 (con un costo total de $85+$29=$114).

En este caso comparativamente es mejor la segunda alterativa.

En el período 3 existen tres alternativas:

emitir un pedido en el período 3 y utilizar la mejor política para los períodos 1 y 2 (a un costo de $102+$114=$216).
o emitir un pedido en el período 2 para los 2 últimos períodos (2 y 3) y utilizar la mejor política para el período 1 considerado de forma independiente (a un costo de $102+$36+$85=$223).
o emitir un pedido en el período 1 para los 3 períodos (con un costo de $85+$29+$36+$36=$186).

En nuestro ejemplo, resulta evidente que no existen incentivos para almacenar productos en inventario en el período 1 o 2 para satisfacer la demanda del período 4, dado que los costos de almacenamiento excederían los costos de emisión de pedido en el período 4. Si lo anterior es cierto, claramente no tiene sentido guardar inventario en el período 1 o 2 para satisfacer demanda de un período superior al 4 (5, 6, 7, etc).

Para los datos propuestos en nuestro ejemplo, la política óptima de pedidos según el Algoritmo de Wagner Whitin es la siguiente:

Pedir 135 unidades (79+56) en el período 11 para satisfacer los requerimientos del período 11 y 12, y utilizar la política óptima para los períodos del 1 al 10.
Emitir un pedido de 67 unidades para el período 10 y utilizar la política óptima de pedidos para los períodos 1 al 9.
Pedir 112 unidades (67+45) en el período 8 para satisfacer la demanda de los períodos 8 y 9, y luego utilizar la mejor alternativa para los períodos del 1 al 7.
Ordenar 121 unidades (61+26+34) en el período 5 para enfrentar la demanda de los períodos 5, 6 y 7.
Pedir 97 unidades (36+61) en el período 3 para satisfacer la demanda de los períodos 3 y 4.
Finalmente pedir 98 unidades (69+29) en el período 1 y con ello cumplir la demanda de los períodos 1 y 2.

La siguiente tabla resume los resultados anteriormente expuestos.

Al pie del cuadro resumen se detalla, por ejemplo, «567 indica la política óptima de pedido para los períodos del 1 al 7 es pedir en el período 5 y satisfacer la demanda de los períodos 5, 6 y 7 y adoptar una política óptima para los períodos 1 al 4 considerados de forma separada».

El costo asociado a implementar el Algoritmo de Wagner y Whitin al problema propuesto como ejemplo es de $864. Se propone al lector corroborar que dicha política minimiza los costos de inventario en comparación a otros sistemas de loteo como Costo Total Mínimo, Costo Unitario Mínimo, EOQ, entre otras.

Una forma de corroborar los resultados obtenidos es mediante una aplicación en Excel que permite automatizar los procesos de cálculo. Básicamente ingresando un inventario inicial (en nuestro ejemplo cero), la demanda pronosticada, los costos de emisión de pedidos y los costos de almacenamiento, se puede fácilmente aplicar una política de lotificación como aquellas que tratamos en extenso en el Plan de Requerimientos de Materiales (MRP).

Observación: La imagen anterior ha sido editada para efectos de una mejor resolución de modo que solo se visualiza los resultados parciales hasta el período 8. El archivo Excel con la aplicación donde se encuentran los resultados del ejemplo desarrollado en este artículo, como también la posibilidad de poder utilizarlo con otras políticas de lotificación se puede descargar a continuación.

[sociallocker]Descarga Aquí el Archivo Excel del Algoritmo de Wagner y Whitin: lotsizing[/sociallocker]

Método de Planos Cortantes (Optimización Dual)

En un tutorial anterior discutimos sobre la Relajación Lagrangeana, y gracias a dicho ejemplo, vimos que al variar los valores de las variables asociadas a la relajación (más conocidos como los Multiplicadores de Lagrange), el valor de la función objetivo del Problema Dual Lagrangeano se va aproximando al valor que se obtiene al resolver el problema original. En palabras simples, lo que se realizó en ese ejemplo fue optimizar los multiplicadores.

En este artículo, lo que veremos es una forma distinta de optimizar dichas variables, mediante un algoritmo que lleva el nombre de Método de Planos Cortantes o Método de Planos de Corte (o simplemente Planos Cortantes). Este algoritmo también se conoce con el nombre de Cortes basados en Descomposición de Benders, y esto es principalmente debido a que este procedimiento utiliza inecuaciones muy similares a las que se ocupan en el método propuesto por J.F. Benders.

La idea fundamental detrás del algoritmo de planos cortantes es comenzar con una solución inicial factible para el problema relajado, para después “cortar” o sacar dicha solución y cambiarla por otra que mejore el valor de la función objetivo que se está optimizando (es decir el valor del Problema Dual Lagrangeano).

Además, para iniciar este método es necesario tener una consideración especial:

El conjunto de puntos que constituyen las soluciones enteras factibles del problema relajado debe ser acotado.

¿Por qué?: Debido a que el algoritmo de planos cortantes utiliza estos puntos, por lo que si el conjunto fuera no acotado, entonces el algoritmo nunca convergería (es decir, nunca terminaría de iterar). Este conjunto acotado se conoce como la envoltura convexa, pero cuidado: no es cualquiera, es la envoltura convexa de las soluciones enteras del problema relajado.

Veamos entonces cómo funciona este método de forma general. Supongamos que tenemos el siguiente problema, en donde el segundo conjunto de restricciones $Cx\leq d$ es “difícil” y complica la resolución, por lo tanto lo sacamos y lo llevamos a la función objetivo, a lo cual llamaremos el problema relajado:

Además, supongamos que es posible enumerar todos los puntos que son factibles para nuestro problema relajado (es decir, los que están dentro de la envoltura convexa). Si pudiéramos hacer eso, entonces bastaría con evaluar en la función objetivo todos esos puntos, y ver cuál entrega el menor valor: este punto sería entonces nuestra solución óptima.

Lo que se menciona anteriormente, se puede representar matemáticamente de la siguiente forma, donde p es la cantidad de puntos que pertenecen a las soluciones enteras de este problema relajado:

Con lo anterior en consideración, podemos entonces expresar nuestro Problema Dual Lagrangeano de la siguiente forma:

Lo cual, se puede volver a reformular y expresar mediante un problema de optimización. Esta reformulación se conoce como el Problema Maestro, en donde ocupamos una variable auxiliar u y queda expresado de la siguiente forma:

Esta reformulación es importante de entender, ya que gracias a que se dispone de cada uno de los puntos que pertenecen a las soluciones enteras del problema relajado (recuerda que dijimos que se podían enumerar), entonces cada una de las restricciones del tipo:

Constituyen un corte para nuestro problema.

Esto nos lleva a la siguiente pregunta: ¿si tenemos todos los puntos, entonces agregamos todos los cortes inmediatamente (simultáneamente)?

La respuesta es NO, ya que esto sería un trabajo muy tedioso, y tomaría mucho tiempo computacional. Para esto existe el algoritmo de los planos cortantes, para ir agregando iterativamente los cortes, de manera tal que tome menos tiempo que agregarlos todos en conjunto.

Como hemos llamado a la reformulación anterior el Problema Maestro, entonces necesitamos un sub-problema, o problema esclavo. Este sub-problema corresponde al problema relajado que discutimos al principio del desarrollo:

Finalmente, la última pregunta que nos podemos hacer es con cuántos cortes partir. Para la pregunta anterior no hay una respuesta que pudiésemos dar a priori como exacta, pero una buena aproximación es que la cantidad de cortes iniciales (o puntos iniciales a utilizar) sea igual a la cantidad de variables o penalizadores, incrementado en una unidad, es decir:

Número de Cortes Iniciales = Número de Penalizadores + 1

Algoritmo de Planos Cortantes

El algoritmo de planos cortantes se puede enunciar mediante los siguientes pasos. Además, luego encontrarás un resumen mediante un diagrama de flujo:

Sea k=1. Sea x1, x2 ,x3 ,…, xr la cantidad de puntos necesarios para iniciar el algoritmo. Crear los cortes del tipo $\mu \leq c^{T}x_{i}+\lambda ^{T}(Cx_{i}-d)$ con dichos puntos.
Resolver el Problema Maestro.
El problema maestro entregará una actualización para los valores de los Multiplicadores de Lagrange. Con ellos, resolver el sub-problema.
Al resolver el sub-problema, se encontrará un nuevo punto perteneciente a las soluciones factibles del problema relajado. Verificar el criterio de parada. Si se cumple, terminar; sino, crear un nuevo corte.
Agregar el corte al Problema Maestro, hacer k=k+1 y volver a 2.

La teoría de este procedimiento puede ser un poco complicada, así que veamos un ejemplo.

Ejemplo Método de Planos Cortantes

Supongamos el siguiente problema de optimización, en donde las primeras cuatro inecuaciones serán las que permanecen en el problema relajado, y las ultimas 4 son las inecuaciones “complicadas” que serán incorporadas a la función objetivo.

Sin embargo, antes de ello presentaremos una representación gráfica del problema propuesto. El área achurada de color verde corresponde al dominio de soluciones factibles de la relajación continua del problema, es decir, omitiendo las condiciones de integralidad para las variables de decisión.

En este contexto la solución óptima de la relajación continua es el vértice B donde x=30/11 e y=42/11, con valor óptimo V(PL)=186/11=16,909 (aprox).

De forma análoga, la solución óptima del problema entero se encuentra identificado con la letra F con x=3 e y=3, siendo el valor óptimo V(PE)=15.

Notar que la representación gráfica anterior y la obtención de la solución óptima de la relajación continua y del modelo de Programación Entera propuesto tiene un fin sólo ilustrativo, de modo que favorezca la comprensión de los conceptos que presentamos más adelante.

A continuación retomamos el procedimiento del Algoritmo de Planos Cortantes. Para ello escribiremos el problema relajado (no confundir con la relajación continua!) de la siguiente forma:

Al escribir este problema, los puntos pertenecientes a la envoltura convexa de las soluciones enteras del problema relajado son los siguientes:

Una representación gráfica de la envoltura convexa del problema relajado se muestra a continuación:

A pesar de que el método sugiere una cantidad de cortes iniciales, como se puede ver en este ejemplo son sólo 8 puntos (denotados por E, F, G, H, I, J más las coordenadas (2,3) y (3,2)), por lo que no seguiremos esta sugerencia. Para iniciar, hacemos k=1 y utilizaremos el punto (1,4) para crear el siguiente corte:

$\mu \geq 14+8\lambda _{1}-4\lambda _{2}+8\lambda _{3}+23\lambda _{4}$

Por lo que el Problema Maestro en la iteración k=1 es:

Al resolver este problema, la solución óptima es: $\lambda_{1}=0,\lambda_{2}=3,5,\lambda_{3}=0,\lambda_{4}=0,\mu=0$ .

Con estos valores para los Multiplicadores de Lagrange, resolvemos el problema relajado:

El cual, entrega como resultado los valores x=5 e y=1, con un valor objetivo de 58,5.

Luego verificamos el criterio de parada ( $0\neq 58,5$ ) por lo que el nuevo punto que nos permite generar un nuevo corte:

$\mu \geq 13+5\lambda _{1}+13\lambda _{2}+\lambda _{3}+24\lambda _{4}$

Hacemos k=2 y el nuevo Problema Maestro es:

Al resolver este problema, la solución óptima es: $\lambda_{1}=0,\lambda_{2}=0,059,\lambda_{3}=0,\lambda_{4}=0,\mu=13,76$ .

Con estos valores para los Multiplicadores de Lagrange, resolvemos el problema relajado:

El cual, entrega como resultado los valores x=2 e y=4, con un valor objetivo de 15,882.

Verificamos el criterio de parada ( $13,76\neq 15,882$ ) por lo que el nuevo punto que nos permite generar un nuevo corte:

$\mu \geq 16+11\lambda _{1}-2\lambda _{2}+7\lambda _{3}+20\lambda _{4}$

Hacemos k=3 y el nuevo Problema Maestro es:

Al resolver este problema, la solución óptima es: $\lambda_{1}=0,\lambda_{2}=0,2,\lambda_{3}=0,\lambda_{4}=0,\mu=15,6$ .

Con estos valores para los Multiplicadores de Lagrange, resolvemos el problema relajado:

El cual, entrega como resultado los valores x=5 e y=1, con un valor objetivo de 15,6, verificamos el criterio de parada (15,6=15,6), por lo que como se cumple el criterio de parada y el algoritmo se detiene.

Al estar optimizando los valores para una Relajación Lagrangeana, hemos encontrado un valor que cumple con lo siguiente:

$Z_{PE}\leq Z_{H}\leq Z_{PL}$

Particularmente para este problema se cumple que:

$15\leq 15,6\leq 16,909$

Mis sinceros agradecimientos a mi amigo Javier Maturana Ross en la elaboración de este artículo, esperando nos pueda seguir contribuyendo con sus aportes y conocimientos al sitio de Gestión de Operaciones.