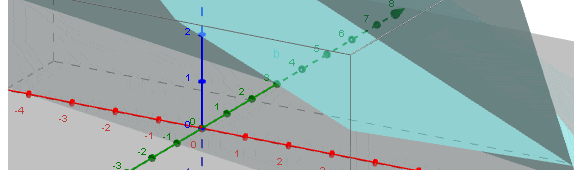
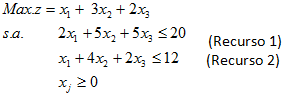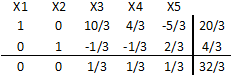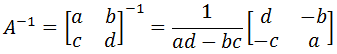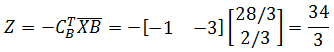El el contexto del Análisis de Sensibilidad en Programación Lineal es usual analizar el impacto que tiene la modificación en la disponibilidad de los recursos en la solución óptima alcanzada originalmente. Esto corresponde al Cambio en el Lado Derecho de las Restricciones (Análisis de Sensibilidad en Programación Lineal). En el siguiente artículo abordaremos el caso cuando cambia un coeficiente o parámetro en el lado izquierdo de las restricciones, generalmente asociado a un coeficiente tecnológico o factor de productividad (por ejemplo, la cantidad de horas hombre que puede requerir la fabricación de un producto, la cantidad de dinero requerido por unidad a producir dada una restricción presupuestaria, entre otras). En relación a lo anterior consideremos el caso de una empresa la cual tiene un plan de producción representado por:
Donde es la cantidad a producir del bien j, z la utilidad de la empresa (en unidades monetarias u.m) y los coeficientes
de las restricciones, la cantidad de recurso i por unidad del producto j. Al aplicar el Método Simplex al modelo anterior incorporando
y
como variables de holgura de las restricciones del recurso 1 y 2 respectivamente, resulta la siguiente tabla final:
Si el requerimiento del primer recurso por parte del producto j=2 cambia de 5 a 2 debido a la incorporación de una nueva tecnología ¿Cambia la actual solución óptima? (,
y
). Sabemos que:
Luego al cambiar un coeficiente en el lado izquierdo asociado a la variable básica , es necesario actualizar la matriz de base inversa o
. Lo anterior se deduce del cálculo de la matriz inversa asociada a la matriz
donde los elementos en la columna correspondiente a los coeficientes en el lado izquierdo (forma estándar del Método Simplex) asociadas a las variables básicas
y
, respectivamente. Finalmente obtenemos la nueva solución básica y verificamos si es factible, esto es si el valor que adopta cada una de las variables básicas satisface las condiciones de no negatividad (en caso que una de las variables básicas alcance un valor negativo se puede continuar las iteraciones con el Método Simplex Dual luego de actualizar el valor de la función objetivo).
En nuestro ejemplo ,
y
lo cual implica que se modifica la solución óptima original pero se conserva la actual base óptima (las mismas variables básicas originales). El nuevo valor óptimo será: