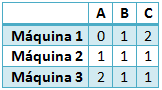
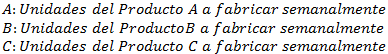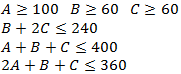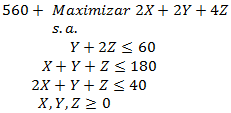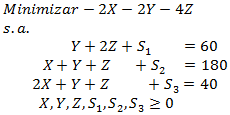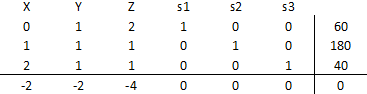Cambio de Variables como Alternativa al Método Simplex de 2 Fases

Una empresa que fabrica tres artículos A, B y C, desea encontrar un Plan de Producción semanal que le permita maximizar sus beneficios netos totales. Los productos son procesados en tres máquinas siendo la producción mínima semanal de 100, 60 y 60 unidades respectivamente. El beneficio neto por unidad vendida de estos artículos son 2, 2 y 4 mil pesos para los artículos A, B y C, respectivamente. Las horas que se necesitan por unidad y máquina son:

Siendo el número de horas disponibles de cada máquina 240, 400 y 360 respectivamente. Formule un modelo de Programación Lineal para abordar el problema propuesto. Resuelva a través del Método Simplex dicho modelo, indicando cuántas unidades de A, B y C se deben fabricar semanalmente y el beneficio final de este plan.

Variables de Decisión: Se debe definir cuántas unidades de cada uno de los 3 productos se fabricarán durante el período de evaluación.

Función Objetivo: Consiste en maximizar el beneficio neto asociado al plan de producción.

Restricciones: Se debe garantizar que se fabrique los mínimos semanales exigidos para cada producto como también que se respete la disponibilidad de horas máquinas.

El problema anterior se puede resolver por el Método Simplex de 2 Fases agregando variables de exceso y auxiliares para cada una de las restricciones que establecen los mínimos semanales de producción. Además se debe agregar variables de holguras para cada una de las restricciones de disponibilidad de horas máquinas. En consecuencia el problema de la Fase 1 tendría 3 variables auxiliares (cuya sumatoria se minimiza en la función objetivo) lo cual genera una instancia de resolución al menos tediosa para este problema (en caso se ser abordada manualmente).

Una alternativa más eficiente de resolución se alcanza al imponer un cambio de variables, lo que permite simplificar las restricciones de mínimos de producción semanal. Sea $X=A-100\geq 0$ , $Y=B-60\geq 0$ y $Z=C-60\geq 0$ . Luego $A=X+100$ , $B=Y+60$ y $C=Z+60$ , obteniendo la siguiente instancia de modelamiento equivalente:

A continuación llevamos a la forma estándar el modelo anterior, transformando la función objetivo a minimización y agregando $s_{1},s_{2},s_{3}$ como variables de holgura de las restricciones 1, 2 y 3, respectivamente:

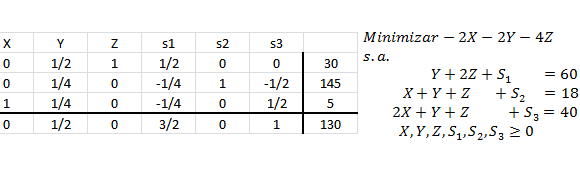
Lo que da origen a la siguiente tabla inicial del Método Simplex:

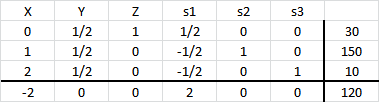
A continuación incorporamos a la base a la variable Z considerando el criterio que favorece la rapidez de convergencia del algoritmo. Luego calculamos el criterio de factibilidad o mínimo cuociente en la columna de la variable Z: $Min\begin{Bmatrix}\frac{60}{2}; \frac{180}{1}; \frac{40}{1}\end{Bmatrix}=30$ , lo que determina que la variable $s_{1}$ deja la base. Se actualiza la tabla realizando una iteración del Método Simplex:

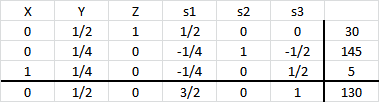
Se procede a incorporar a la variable $X$ a la base y $s_{3}$ abandona la base dado que $Min\begin{Bmatrix}\frac{150}{1}; \frac{10}{2}\end{Bmatrix}=5$ . Se realiza una iteración adicional que permite alcanzar la siguiente solución básica factible óptima:

La solución óptima es $X=5$ , $Y=0$ y $Z=30$ que al remplazar en las variables originales permite obtener $A=X+100=5+100=105$ , $B=Y+60=0+60=60$ y $C=Z+60=30+60=90$ . Notar que el valor óptimo es $V(P)=130+560=690$ luego de sumar el valor de la constante 560 al valor obtenido para la función objetivo del problema auxiliar. Se propone al lector corroborar los resultados anterior a través de la aplicación del Método Simplex de 2 Fases que por cierto permite alcanzar idénticos resultados pero con una mayor esfuerzo en la resolución.

Rating: 3.0/5. From 2 votes.

Please wait...

Cambio de Variables como alternativa al Método Simplex de 2 Fases

Deja una respuesta Cancelar la respuesta