La Programación Lineal nos permite abordar distintos problemas de naturaleza real algunos de los cuales ya hemos tratado en artículos anteriores como el Problema de Transporte, el Problema de Mezcla de Productos y el Problema de la Dieta.
En el siguiente artículo analizaremos otra aplicación clásica conocida como el Problema de Producción e Inventario cuyas extensiones y variantes se pueden consultar adicionalmente en la categoría del Plan Maestro de la Producción.
El Problema de Producción e Inventario consiste básicamente en determinar una política de producción en el tiempo que permita satisfacer ciertos requerimientos de demanda, respetando las limitantes de producción y a un costo mínimo.
Este tipo de modelos se puede extender para varios productos, sin embargo, en esta oportunidad consideraremos un solo producto para su ilustración.
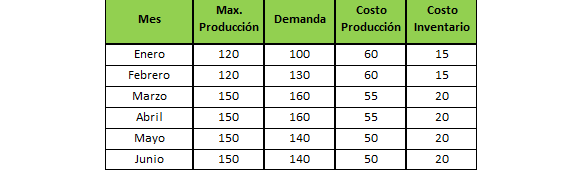
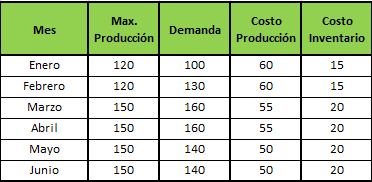
En este contexto, consideremos los siguientes antecedentes de producción que se presentan a continuación:
Luego, definimos el siguiente modelo de optimización lineal:
Supuesto: se dispone de un inventario inicial de 50 unidades, es decir, I0=50.
1. Variables de Decisión:
- Xt: Unidades a producir en el mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)
- It: Unidades a almacenar en inventario al final del mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)
2. Función Objetivo: Minimizar los costos de producción (destacados con color azul) y costos de inventario (destacados con color rojo) durante el período de planificación definido por:
60X1 + 60X2 + 55X3 + 55X4 + 50X5 + 50X6 + 15I1 + 15I2 + 20I3 + 20I4 + 20I5 + 20I6
De forma compacta (parametrica) se puede representar la función objetivo como:
Donde es el costo unitario de producción en el mes t (por ejemplo
) y
es el costo unitario de almacenar unidades en inventario durante el mes t (por ejemplo
)
3. Restricciones:
a) Satisfacer los requerimientos de demanda (conocida como restricción de Balance de Inventario).
Por ejemplo, el inventario disponible al final del mes de Enero será el resultado de la producción del mismo mes, más el inventario inicial (que se asume un dato, en este caso 50 unidades) menos la demanda satisfecha durante el mes de Enero.
- X1 + 50 – I1 = 100 (Enero)
- X2 + I1 – I2 = 130 (Febrero)
- X3 + I2 – I3 = 160 (Marzo)
- X4 + I3 – I4 = 160 (Abril)
- X5 + I4 – I5 = 140 (Mayo)
- X6 + I5 – I6 = 140 (Junio)
Notar que la restricción se Balance de Inventario impuesta para un producto se puede generalizar como: , donde
representa la demanda estimada (parámetro) para el mes t.
b) Respetar la capacidad máxima de producción mensual (oferta).
Se establece que la oferta o producción máxima mensual no puede superar la capacidad de producción.
X1<=120 X2<=120 X3<=150 X4<=150 X5<=150 X6<=150
O simplemente donde
es la capacidad de producción máxima del mes t (parámetro).
c) Condiciones de no negatividad.
De forma natural y dada nuestra definición cada variable de decisión debe ser no negativa.
Xt >= 0 It >= 0 Para todo t
El siguiente tutorial muestra cómo implementar este Modelo de Producción e Inventario correspondiente a la Programación Lineal en Solver de Excel:
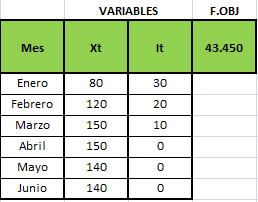
La solución óptima se muestra a continuación con un valor óptimo de $43.450. Se puede apreciar que se producen en total 780 unidades entre Enero y Junio las cuales junto al inventario inicial de 50 unidades permiten satisfacer los requerimientos de demanda mensualmente.
¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.
[sociallocker]
MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO
[/sociallocker]
Excelente planteamiento, es claro pero seria conveniente hacer resolución de problemas de manera canónica y luego formularlas en compacto, debido a que de esta forma se puede programar en cualquier soft. que al final es lo mas utilizados a parte del Solver….
Saludos
Hola
Con respecto al problema de producción e inventario tengo dudas respecto a las restricciones ( mencionan que es restricciones de balance de inventario). son estas: X1 + 50 – I1 = 100 (Enero)X2 + I1 – I2 = 130 (Febrero)X3 + I2 – I3 = 160 (Marzo) X4 + I3 – I4 = 160 (Abril)X5 + I4 – I5 = 140 (Mayo)X6 + I5 – I6 = 140 (Junio)
>Entiendo que para satisfacer la demanda debo tener x mas el inventario inicial que es de 50, pero no entiendo porque se resta I1. Espero y puedan explicarme por favor.
Hola Edber
Las restricciones de balance de inventario son de la forma:
Xt + It-1 – It = dt
Al rescribir la restricción despejando el inventario al final de cada período se obtiene:
It = Xt + It-1 – dt
Que se interpreta como que el inventario al final de cada período corresponde a la producción del mismo período más el inventario inicial y menos la demanda del período. Por ejemplo el inventario que se obtendrá al final del mes de Mayo será igual al inventario inicial de ese mes (o lo que quedo a fines de Abril) más la producción de Mayo y menos la demanda satisfecha durante ese mes.
como puedo interpretar las dos columnas Lizq Lder
@edwin
El Lado Izquierdo en la planilla corresponde al valor que adopta la restricción al ser evaluada en la solución del problema. Por tanto vincula tanto los parámetros de las restricciones y las variables de decisión según se detalla en el modelo.
El Lado Derecho es el parámetro o constante que define las condiciones del problema (por ejemplo la demanda de cada período).
Saludos
El Equipo de Gestión de Operaciones
¿Cómo se representaría la función objetivo por favor?
@Katerin. La forma funcional de la función objetivo se detalla en el artículo y corresponde a la suma de los costos de producción y mantención de inventario para el horizonte de planificación de 6 meses (Enero a Junio).
¿Por qué las restricciones están igualadas (=) en lugar de estar con mayor e igual, lo digo considerando que en el mes 2 se debe producir suficiente para satisfacer parte del mes 3?
@Carlos. No es necesario establecer la restricción de balance de inventario como «mayor e igual». Como bien observas en algunos períodos es necesario producir más de la demanda del mes correspondiente dado que se debe almacenar inventario para satisfacer los requerimientos de períodos futuros. Por tanto el inventario como variable asume dicha función.