En Programación Lineal una Solución Básica Factible (SBF) es aquella que además de pertenecer a la región o área factible del problema se puede representar a través de una solución factible en la aplicación del Método Simplex satisfaciendo las condiciones de no negatividad.
En este contexto una solución básica factible corresponderá a uno de los vértices del dominio de factibilidad cuya coordenada o solución se puede representar a través de un conjunto de restricciones activas para el modelo.
Para desarrollar el concepto anterior consideremos el siguiente problema de optimización matemática (lineal):
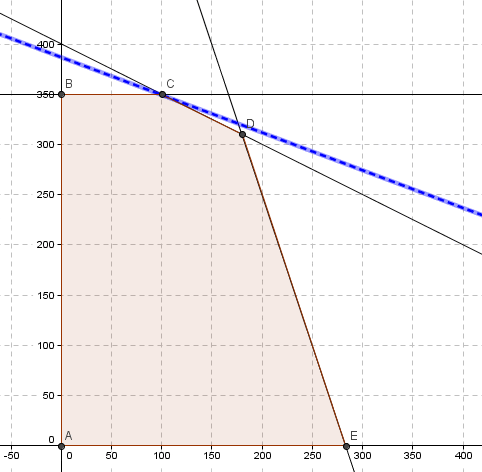
La resolución gráfica del problema anterior haciendo uso de Geogebra se presenta en el siguiente gráfico:
El área achurada corresponde al dominio de factibilidad del problema, identificándose en particular 5 vértices que hemos llamado arbitrariamente A, B, C, D y E.
La solución óptima del modelo lineal se alcanza en el vértice C donde X=100 e Y=350 con valor óptimo V(P)=3.100. Notar que dicha solución se puede obtener a través de la resolución de un sistema de ecuaciones con las restricciones 1 y 3 (R1 y R3) en igualdad.
En consecuencia, el vértice C además de ser una solución básica factible es una solución básica factible óptima.
En cuanto a los vértices A, B, D y E son soluciones básicas factibles (no óptimas) debido a que en la aplicación del Método Simplex al menos una variable no básica tendrá costo reducido negativo (lo que permitirá mejorar el actual valor de la función objetivo).
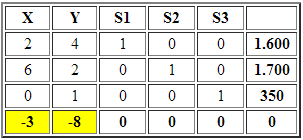
La tabla a continuación es la que se obtiene al llevar al problema a su forma estándar, agregando S1, S2 y S3 como variables de holgura de las restricciones 1, 2 y 3, respectivamente (R1, R2 y R3).
Ambas variables no básicas (iniciales) X e Y tienen costo reducido negativo (-3 y -8) por tanto X=0 e Y=0 que si bien es una solución básica factible (vértice A) no es solución óptima.
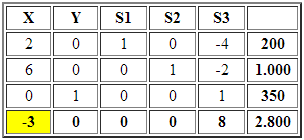
Para continuar la demostración realizaremos una iteración del Método Simplex incorporando la variable Y a la base (criterio costo reducido «más negativo«) y donde el mínimo cuociente Min {1.600/4; 1.700/2; 350/1}=350 ==> S3 deja la base:
La solución básica factible ahora es X=0 e Y=350 (vértice B), sin embargo, el costo reducido de la variable X sigue siendo negativo y por tanto aún no nos encontramos en el óptimo. En consecuencia X entra a la base y obtenemos el mínimo cuociente: Min {200/2; 1.000/6}=100 ==> S1 deja la base:
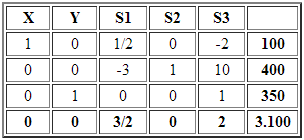
Finalmente se alcanza la solución óptima (solución básica factible óptima) con X=100 e Y=350 (vértice C) donde todas las variables no básicas (S1 y S3) tienen costos reducido mayor o igual a cero, cumpliendo con el criterio de optimalidad.
¿Qué sucede con los vértices D y E? También son soluciones básicas factibles (no óptimas) que se podrían encontrar por ejemplo incorporando en primera instancia (tabla inicial) a la variable X a la base. De esta forma se debería alcanzar el vértice E luego de una iteración y el vértice D en una segunda iteración.
Notar que también existen otras soluciones factibles (no básicas) como, por ejemplo, X=100 e Y=100 que pertenecen al dominio de soluciones factibles pero no se puede representar a través de la resolución de un sistema de ecuaciones.