En los cursos básicos de Investigación de Operaciones (o Investigación Operativa) frecuentemente el tema de introducción y discusión inicial es la formulación y resolución de modelos de optimización lineales para apoyar el proceso de toma de decisiones.
En este contexto se suelen abordar formulaciones matemáticas sencillas como los cubiertas en Programación Lineal y para entender sus propiedades se estudian modelos que consideran 2 variables de decisión para que sea factible y sencillo representarlos gráficamente, de modo de encontrar su solución óptima y valor óptimo (en caso de existir).
Al respecto cabe destacar que aquellas propiedades que se desprenden de la resolución gráfica de modelos lineales se pueden extender a problemas de Programación Lineal de mayor tamaño. Algunos de estos aspectos se detallan en el artículo Teorema Fundamental de la Programación Lineal.
A continuación presentaremos un modelo de Programación Lineal con 2 variables de decisión el cual resolveremos con la ayuda del software libre Geogebra, el cual es muy útil para la representación gráfica de funciones matemáticas, figuras geométricas, entre otras.
El programa se puede descargar gratuitamente tanto a computadores o smartphones, o si se prefiere, ejecutar directamente desde su página www.geogebra.org en Internet.
El siguiente tutorial de nuestro canal de Youtube muestra como resolvemos gráficamente este modelo de Programación Lineal utilizando el software Geogebra.
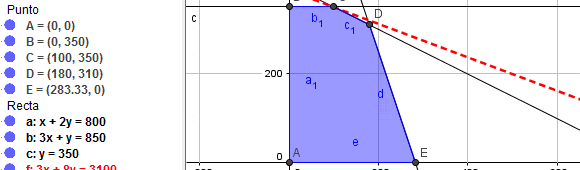
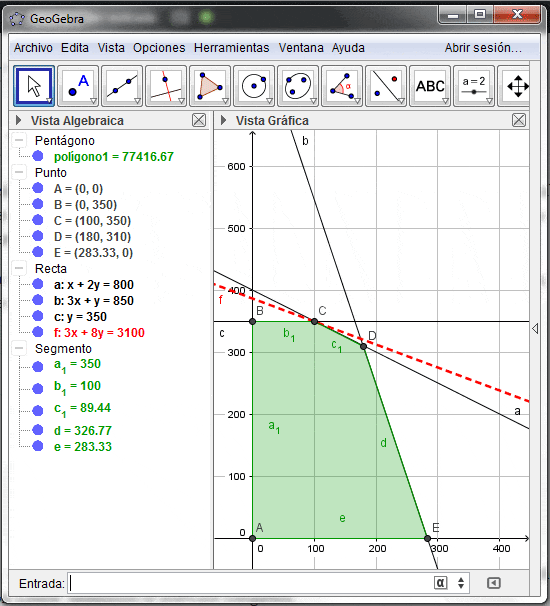
Una vista final de la representación gráfica del problema lineal propuesto se presenta a continuación:
Con color verde se destaca el polígono que considera todas aquellas soluciones factibles del problema, es decir, aquellos valores para las variables de decisión que satisfacen de forma simultanea el conjunto de restricciones. Dicho dominio de factibilidad se denomina región de puntos factibles o dominio de soluciones factibles.
Adicionalmente con color rojo se observa una linea punteada que representa la curva de nivel de la función objetivo que intercepta el vértice óptimo (solución óptima). La solución óptima es y
, con valor óptimo
.
Cabe destacar que existen otras herramientas gráficas que permiten resolver gráficamente un modelo de Programación Lineal en 2 variables. Tal es el caso del software TORA el cual se incluye en el libro de Investigación de Operaciones de H.Taha (ver Cómo Resolver Gráficamente un Modelo de Programación Lineal con TORA) y IORTutorial (Cómo Resolver Gráficamente un Modelo de Programación Lineal con IORTutorial).

Excelente artículo. Ayuda bastante saber que existen herramientas que son útiles para resolver modelos de optimización de forma sencilla.