Existen algunas herramientas en Internet que permiten resolver modelos de Programación Lineal utilizando el Método Simplex. Este tipo de aplicaciones resultan de bastante utilidad para los estudiantes de ingeniería que desean verificar si los resultados que obtienen en la aplicación manual del método resultan ser correctos.
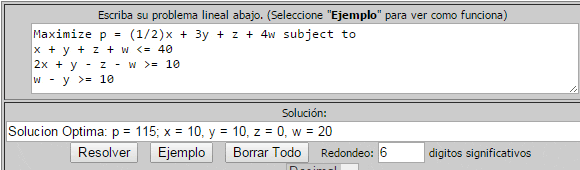
En esta oportunidad revisaremos la interfaz para resolver modelos de Programación Lineal con el Método Simplex disponible en el sitio web ProgramacionLineal.net. Para ello utilizaremos un modelo lineal en 2 variables que previamente resolvimos gráficamente con el complemento Solver de Excel y el software Geogebra.
Cómo resolver un modelo de Programación Lineal con el Método Simplex
El siguiente tutorial muestra cómo implementamos este modelo de optimización con la herramienta de resolución del Método Simplex:
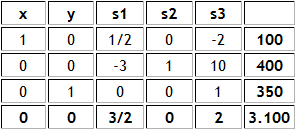
La última tabla del Método Simplex luego de la resolución con esta aplicación y eliminando la columna p (no es necesaria) es la siguiente:
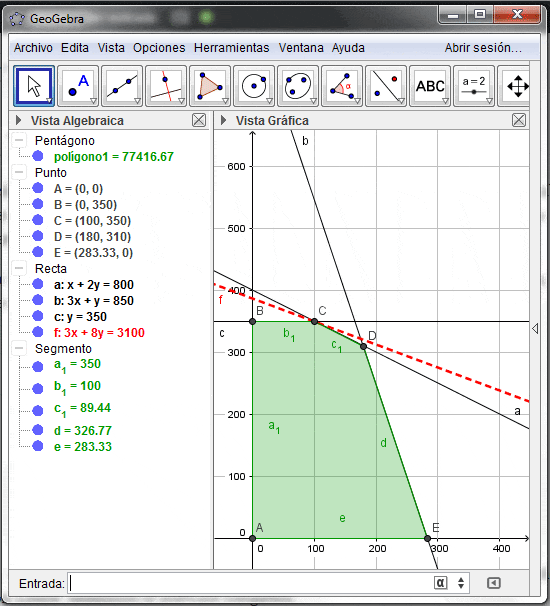
La Solución Óptima (que corresponde a una solución básica factible óptima) es x=100 e y=350 (x e y son las variables básicas de las filas 1 y 3 respectivamente). El valor óptimo es V(P)=3.100. Notar que la solución óptima corresponde al vértice C de la representación gráfica del problema propuesto que se muestra a continuación:
Importante: Las variables s1 y s3 son variables no básicas en la actual solución óptima y por tanto su valor es cero. La variable s2 es la variable básica de la fila 2 y toma el valor de 400. Notar que las variables s1, s2 y s3 son inicialmente las variables de holgura necesarias para llevar el modelo de Programación Lineal a su forma estándar.