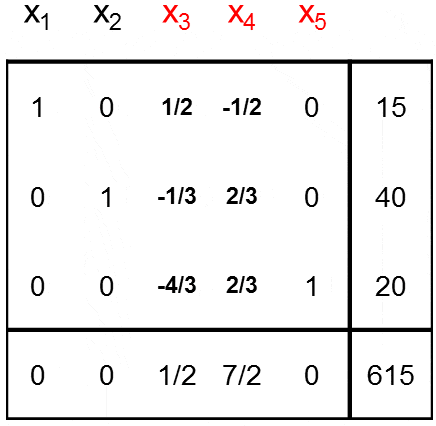
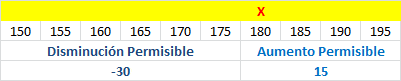
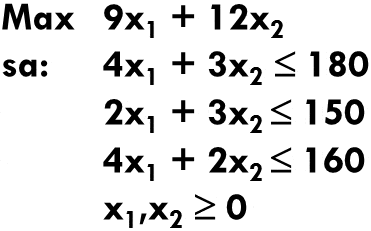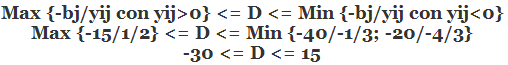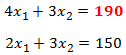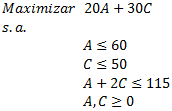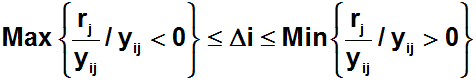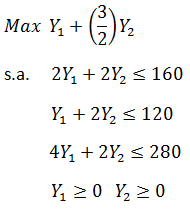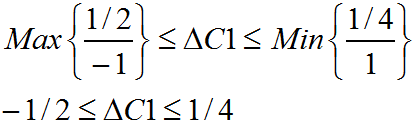análisis de sensibilidad Archivos - Página 2 de 4

Problema de Arriendo de Buses para Transporte de Pasajeros en Programación Lineal

El siguiente problema de Programación Lineal consiste en determinar una política óptima de arriendo de buses para el transporte de pasajeros que minimice los costos asociados a su arriendo y satisfaga los requerimientos de transporte y otras condiciones adicionales que se deseen imponer.

El Centro de Alumnos de Ingeniería Industrial de una respetada universidad desea celebrar el día del alumno en la playa. Este paseo está planificado para 1.200 alumnos como mínimo. Una empresa de transporte ofrece 2 tipos de buses pero solo cuenta con 28 conductores. La tabla de abajo indica la capacidad y el costo de arriendo de cada tipo de bus:

Para mantener el equilibrio de su flota, la empresa de transporte impone la condición de que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. Formule y resuelva un modelo de Programación Lineal que permita determinar cuántos buses de cada tipo hay que arrendar para el paseo de modo que resulte lo más económico para el Centro de Alumnos.

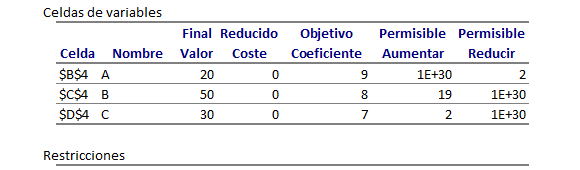
Variables de Decisión:

$x$ : Cantidad de Buses Tipo A arrendados
$y$ : Cantidad de Buses Tipo B arrendados

Función Objetivo:

Minimizar $80.000x+110.000y$

Restricciones:

Cantidad de Alumnos: $40x+60y\geq 1.200$
Cantidad de Conductores: $x+y\leq 28$
Condición de Flota: $x-y\geq 0$
No Negatividad: $x,y\geq 0$

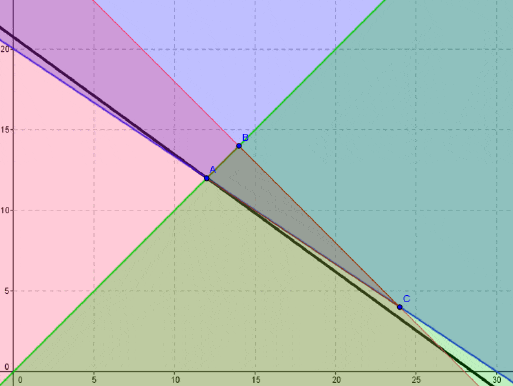
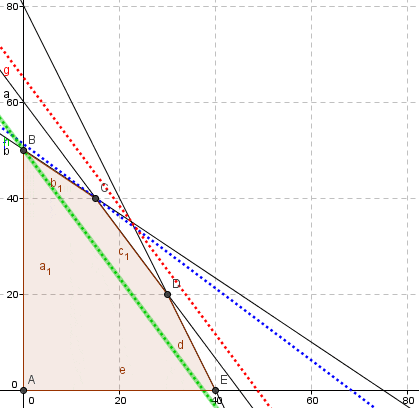
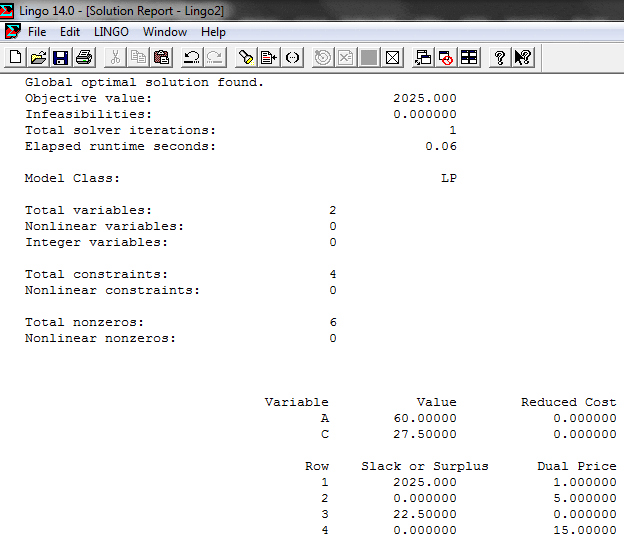
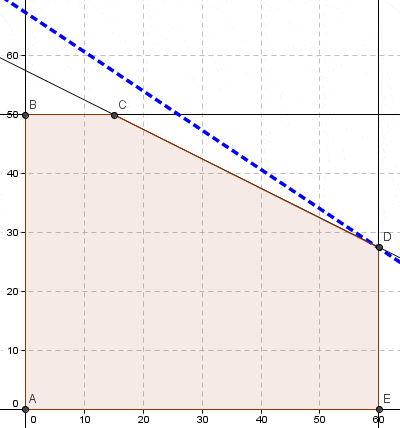
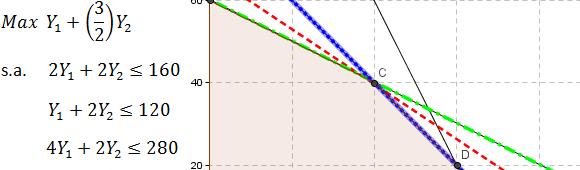
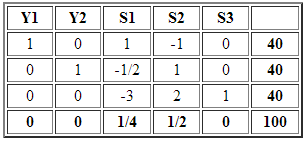
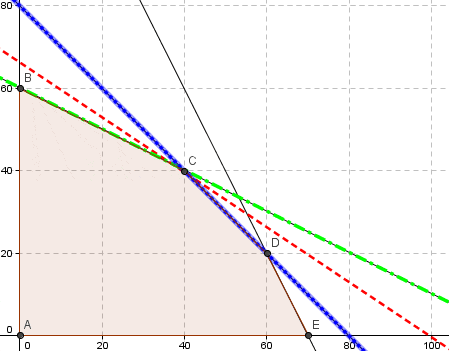
El dominio de soluciones factibles del problema esta dado por el polígono ABC según se detalla a continuación (representación gráfica realizada con el software Geogebra). En particular la solución óptima corresponde al vértice A donde $x=12$ e $y=12$ , con valor óptimo $V(P)=80.000*12+110.000*12=2.280.000$ .

Notar que si bien el problema fue modelado como uno de Programación Lineal, dadas las características del problema sería deseable obtener una solución entera para las variables de decisión (dado que no es posible arrendar una fracción de buses y asumir por ejemplo que el costo del mismo es proporcional a la capacidad ocupada). No obstante en el ejemplo propuesto la solución óptima obtenida cumple de forma natural con las condiciones de integralidad, lo que indica que sus resultados son idénticos al problema de Programación Entera asociado (es decir, aquel al cual se le agregan de forma explícita las condiciones de enteros para las variables de decisión).

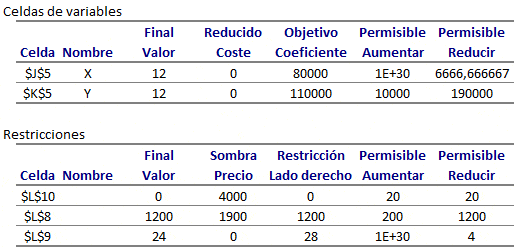
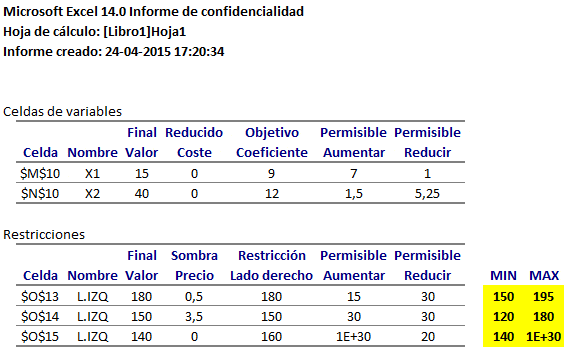
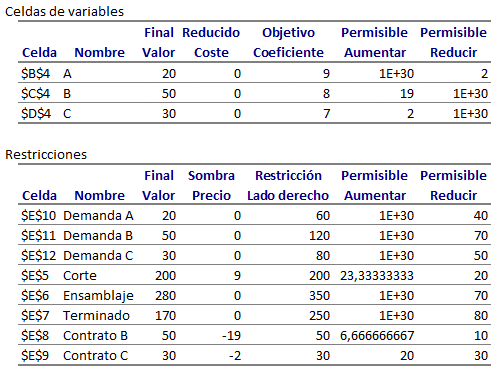
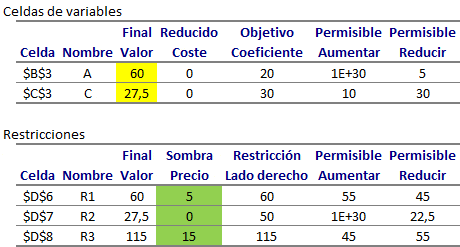
De forma complementaria al análisis anterior se pueden responder las siguientes preguntas correspondientes al análisis de sensibilidad o postoptimal:

1. Determine cuánto podría variar el costo de arriendo del Bus tipo A que conserve la solución óptima. Si C1 (costo arriendo del Bus tipo A) varía en el intervalo entre [73.333,3 , ∞[ se conserva la actual solución óptima.

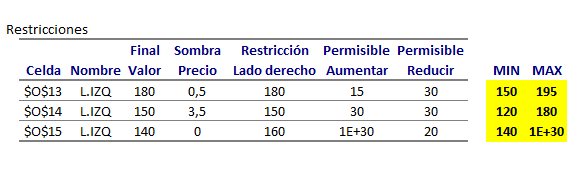
2. Determine el impacto en el valor óptimo del problema si se elimina la condición que el número de buses tipo B arrendados no puede exceder el número de buses tipo A arrendados. El precio sombra de la restricción de condición de flota es 4.000. Luego si se elimina la condición de flota la solución óptima se alcanza en la mínima variación $(x,y)=(0,20)$ para una reducción permisible del lado derecho de dicha restricción en 20 unidades. Luego el nuevo valor óptimo es $V(P)=2.280.000+(-20-0)*4.000=2.200.000$ .

Cálculo del Intervalo de Variación del Lado Derecho que conserva la Base Óptima

Una vez concluidas las iteraciones del Método Simplex y en el caso de alcanzar una solución básica factible óptima, puede resultar de interés determinar un intervalo de variación para un parámetro del vector de los lados derechos de las restricciones que permita conservar la geometría del problema. Esto implica que se conservan las restricciones activas originales en el nuevo escenario (es decir, se mantiene la base óptima) que se genera a partir de la modificación (individual) de un parámetro o coeficiente del lado derecho. Para ilustrar el resultado anterior consideremos el siguiente modelo de Programación Lineal.

Luego de llevar a la forma estándar el modelo anterior agregando $x_{3}$ , $x_{4}$ y $x_{5}$ como las variables de holgura de las restricciones 1, 2 y 3, respectivamente, y aplicar las iteraciones necesarias del Método Simplex, se alcanza la siguiente tabla final (óptima):

La solución óptima es $x_{1}=15$ y $x_{2}=40$ con valor óptimo $V(P)=615$ . El valor de las variables de holgura en el óptimo $x_{3}$ , $x_{4}$ y $x_{5}$ es 0, 0 y 20, respectivamente. Luego se puede concluir que la solución óptima del problema se alcanza con las restricciones 1 y 2 activas (notar que sus respectivas holguras con variables no básicas en el óptimo) y la base actual esta conformada por las variables $x_{1}$ , $x_{2}$ y $x_{5}$ .

Sabemos adicionalmente que, por ejemplo, el costo reducido de la variable de holgura $x_{3}$ representa el precio sombra asociado a la primera restricción ( $\pi_{1}=1/2$ ). No obstante desconocemos en qué intervalo puede variar el parámetro del lado derecho de la restricción 1 (actualmente $b_{1}=180$ ) de modo que se conserve la base óptima y por tanto nos permita hacer un correcto uso de la información del precio sombra.

Para ello se propone la siguiente fórmula que permite encontrar el intervalo de variación para un lado derecho que conserva la base óptima:

Max {-bj/yij con yij>0} <= D <= Min {-bj/yij con yij<0}

Por ejemplo determinemos el intervalo para el parámetro $b_{1}$ :

En consecuencia $b_{1}$ puede disminuir en 30 unidades y aumentar en 15 unidades y se conserva la base óptima. Es decir, si $b_{1}\epsilon [150,195]$ se mantiene la base óptima.

El resultado anterior se puede corroborar gráficamente. La solución óptima se encuentra en el vértice C donde las restricciones 1 y 2 son activas (notar la curva de nivel que pasa por el vértice óptimo es la línea punteada de color azul). Si para el lado derecho de la restricción 1 consideramos $b_{1}=150$ se obtiene la línea de color verde y para $b_{1}=195$ la línea de color rojo. En estos casos si bien se modifica el dominio de soluciones factibles, la solución óptima conserva las actuales restricciones activas (y por ende cuando $b_{1}$ adopta un valor fuera de este intervalo cambia la geometría del problema o base óptima).

Esto es consistente con el Informe de Confidencialidad de Solver. En particular el reporte de restricciones donde se aprecia el aumento y reducción permisible que conserva la actual base óptima:

Por ejemplo, ¿cuál es el nuevo valor óptimo si el lado derecho de la restricción 1 ahora es $b_{1}=190$ ?. Como $b_{1}=190\epsilon[150,195]$ , entonces $V(P)=615+\Delta b_{1}\pi _{1}=615+(190-180)*(1/2)=620$ . ¿Cuál es la nueva solución óptima?. Como sabemos que se conservan las restricciones activas en el óptimo para la variación propuesta, la solución óptima del nuevo escenario se obtiene simplemente resolviendo el siguiente sistema de ecuaciones (notar que la restricción 1 y 2 se conservan activas):

De donde $x_{1}=20$ y $x_{2}=110/3$ , que al evaluar en la función objetivo se obtiene: $V(P)=9*(20)+12*(110/3)=620$ corroborando el resultado anterior. Dejamos al lector el desafío de aplicar los conceptos presentados en este articulo para encontrar un intervalo para $b_{2}$ y $b_{3}$ que conserve la base óptima.

Informe de Confidencialidad de Celdas de Variables y Restricciones de Solver

El siguiente problema tiene por objetivo mostrar la interpretación del Informe de Confidencialidad (o Informe de Sensibilidad) de Solver de Excel en los distintos escenarios que de éste se pueden considerar. Una empresa fabrica 3 productos (A, B y C) y desea planificar la producción semanal de cada uno de estos productos. Para ello dispone de 200 horas semanales en el departamento de corte, 350 horas semanales en el departamento de ensamblaje y 250 horas semanales en el departamento de terminado. Cada producto utiliza una determinada cantidad de horas en estos departamentos según lo muestran los parámetros en el lado izquierdo de las respectivas restricciones. Adicionalmente la empresa ha adquirido contratos con clientes que compran el producto B y C para producir al menos 50 y 30 unidades semanales, respectivamente. Finalmente según el departamento de ventas se ha estimado que la demanda máxima semanal para los productos A, B y C son 60, 120 y 80 unidades respectivamente.

Un modelo de Programación Lineal para la situación anterior es:

Luego de implementar en Solver de Excel el modelo anterior se obtiene el siguiente Informe de Confidencialidad (Informe de Sensibilidad):

1. ¿Cuánto estaría dispuesto a pagar para cancelar el contrato que obliga a producir al menos 30 unidades de C?

El Precio Sombra de la restricción de contrato del producto C es de -2 y su disminución permisible es de 30 unidades. Por tanto podemos utilizar el precio sombra para predecir el cambio en el valor óptimo ante la eliminación de este contrato (que sería equivalente a reemplazar $C\geq 30$ por $C\geq 0$ ). El valor óptimo en consecuencia aumentaría en -2*(0-30)=$60 que determina la máxima disposición a pagar para eliminar este contrato.

2. Suponga que se elimina el contrato que obliga producir al menos 50 unidades de B. ¿Cuál es el impacto en el impacto en el valor óptimo?

El Precio Sombra de la restricción de contrato del producto B es de -19 y su disminución permisible es de 10 unidades. Esto determina que reemplazar $B\geq 50$ por $B\geq 0$ no llevaría la producción de B a cero sino que sólo disminuiría a 40 unidades. Por tanto al eliminar este contrato el valor óptimo aumentaría en -19*(40-50)=$190 que determina la máxima disposición a pagar para eliminar este contrato.

3. Suponga que la empresa tiene $100 para invertir en capacidad. El costo de una hora extra de capacidad en los departamentos de Corte, Ensamblaje y Terminación es de $7, $5, y $6 respectivamente. ¿Cómo invertiría los fondos?. Asuma que sólo puede invertir en una de las 3 alternativas.

No tiene sentido destinar fondos adicionales para contratar horas extraordinarias en los departamentos de ensamblaje y terminado dado que en la actual solución óptima éstas restricciones no se encuentran activas y por tanto existen horas ociosas en dichos departamentos (70 y 80 horas semanales, respectivamente).

Por el contrario el departamento de corte se encuentra operando a máxima capacidad y dispone de un precio sombra de $9 que es mayor al costo de la hora extra de $7, por lo tanto conviene comprar capacidad adicional.

Con un presupuesto de $100 se pueden adquirir 14,2857 horas adicionales en el departamento de corte ($100/7) lo cual está dentro del aumento permisible para el precio sombra (23,3 horas) por tanto se destina la totalidad del presupuesto para dicho propósito.

4. ¿Cuál es el rango de variación para el coeficiente asociado a la variable B en la función objetivo que conserva la actual solución óptima?

Notar que la solución óptima actual es A=20, B=50, C=30. Adicionalmente el valor actual del parámetro en la función objetivo que pondera la variable B es 8, con un aumento permisible de 19 y una reducción permisible de 1E+30 (infinito). Es decir, el intervalo de variación para el parámetro que conserva la solución óptima es ]-1E+30,27]. La cota inferior del intervalo anterior cobra sentido al considerar la restricción de Contrato de B, que, independiente del beneficio (o pérdida) que reporte dicho producto al plan de producción, se debe fabricar de todos modos.

Como resolver un modelo de Programación Lineal con LINGO 14.0

LINGO es un popular software de optimización matemática para uso tanto académico como empresarial desarrollado por LINDO Systems Inc (quienes desarrollaron What’sBest!) que provee una alternativa para enfrentar el problema de modelamiento matemático e implementación computacional en una plataforma distinta a Excel (en contraste a los complementos que han tenido un lugar preferente en nuestro sitio como Solver, Premium Solver Pro, What’sBest! y OpenSolver).

En el siguiente artículo detallaremos cómo descargar e instalar el programa LINGO para luego utilizar éste en la resolución de un modelo de Programación Lineal con 2 variables de decisión. Dado lo anterior consideremos el siguiente problema:

Paso 1: Descarga e instalar la última versión disponible de LINGO desde la sección de descargas del sitio web de LINDO Systems. Se debe tener especial atención en seleccionar de forma correcta la versión compatible con nuestro sistema operativo (Windows o Linux) y la cantidad de bits asociado a dicho sistema. Para verificar este último aspecto te recomendamos leer el artículo “Cómo descargar e instalar la versión de Prueba de What’sBest! 11.1 en Excel 2010”. En dicho artículo se detalla adicionalmente el procedimiento de registro y activación de la licencia.

Paso 2: Una vez instalado LINGO en nuestro computador ejecutamos el programa y luego implementamos el modelo de optimización. El software es compatible con distintos tipos de sintaxis las cuales iremos abordando en próximos artículos en el Blog). Por el momento a continuación detallamos una notación intuitiva que nos permite representar nuestro ejemplo:

Una vez incorporado definido el problema ejecutamos el botón “Solve”:

Paso 3: Se obtienen los resultados para el modelo. La ventana “Lingo 14.0 Solver Status” detalla las características del problema: LP (Programación Lineal) con Valor Óptimo de 2.025.

El detalle de los resultados se aprecia en el informe de respuestas que genera el programa de forma automática. La salida computacional se muestra a continuación:

La Solución Óptima es A=60 y C=27,5 con Valor Óptimo V(P)=2.025. Notar adicionalmente que los resultados son consistentes con los que obtendríamos de utilizar Solver para este ejemplo y haciendo uso del Informe de Confidencialidad (Sensibilidad).

Con color verde destacamos el precio sombra de cada una de las restricciones del problema. Estos valores se identifican en la columna etiquetada “Dual Price” en el informe de resultados de LINGO en las Filas (Row) 2, 3 y 4, respectivamente.

Una representación gráfica del problema anterior con Geogebra nos permite corroborar los resultados anteriores de forma intuitiva, por ejemplo la restricción C<=50 no está activa, en consecuencia su precio sombra es igual a cero.

Cambio en un coeficiente de la Función Objetivo asociado a una Variable Básica

En el contexto del Análisis de Sensibilidad o Postoptimal en Programación Lineal y una vez alcanzada la tabla (tableau) final en la aplicación del método simplex, resulta de interés evaluar el impacto en la solución óptima del problema si cambia un coeficiente o parámetro en la función objetivo asociado a una variable básica. Se busca dar respuesta a este escenario sin la necesidad de reoptimizar, es decir, de resolver el problema original nuevamente.

Para conservar la solución óptima identificada inicialmente, se debe cumplir que el costo reducido de todas las variables debe ser mayor o igual a cero (recordar que el costo reducido de las variables básicas es cero por tanto dicha condición en la práctica se establece sobre las variables no básicas). Lo anterior se garantiza si el incremento es cualquiera en el siguiente intervalo:

Donde rj es el costo reducido de la respectiva variable no básica en la actual solución óptima y los coeficientes yij denotan las entradas en la tabla final del método simplex asociadas a la variable básica xi (cuyo costo cambia) y la respectiva variable no básica xj.

Para presentar el concepto anteriormente expuesto consideremos el siguiente problema de Programación Lineal:

Luego de llevar a la forma estándar, incorporando S1, S2 y S3 como las variables de holgura de las restricciones 1, 2 y 3 respectivamente y resolver el modelo lineal anterior a través del método simplex se alcanza la siguiente tabla óptima:

La solución básica factible óptima es Y1=40 e Y2=40 con valor óptimo V(P)=100. A continuación determinaremos un intervalo de variación para los coeficientes que ponderan a las variables Y1 e Y2 en la función objetivo de modo que conservar la actual solución óptima. En este sentido tanto Y1 como Y2 son variables básicas en el óptimo según se aprecia en la tabla anterior.

Luego el intervalo de variación para C1 (en adelante coeficiente asociado a la variable Y1 en la función objetivo de minimización) que mantiene la solución óptima original es:

Del cálculo anterior se obtiene que C1 (coeficiente que multiplica a la variable Y1 en la función objetivo de minimización) puede variar en el intervalo entre C1℮[-1-1/2, -1+1/4], es decir, C1℮[-3/2, -3/4] y se conserva la actual solución óptima. Si hacemos la equivalencia en la función objetivo de maximización original el intervalo corresponde a C1℮[3/4, 3/2], es decir, existe una reducción permisible de 1/4 y un aumento permisible de 1/2 para el valor actual del parámetro que mantiene la solución óptima inicial. De forma análoga se puede verificar que el intervalo de variación para C2 (en la función objetivo de maximización) corresponde a C2℮[1, 2], con un aumento y disminución permisible de 1/2 en cada caso.

Los resultados obtenidos son consistentes con los que provee el informe de confidencialidad o sensibilidad de Solver según se resume a continuación:

Una alternativa para corroborar los resultados anteriores de una forma intuitiva consiste en realizar una representación gráfica del problema anterior. La solución óptima se encuentra en el vértice C, donde la línea punteada de color rojo representa la curva de nivel que intersecta dicha solución. Por otra parte la línea punteada de color verde se obtiene al modificar C1 a 3/4 (reducción permisible de 1/4), lo cual conserva la solución óptima actual pero deja de ser única (en efecto se genera el caso de infinitas soluciones óptimas en el tramo entre los vértices B y C). Finalmente la línea color azul representa la curva de nivel que resulta de cambiar el coeficiente de C1 a 3/2 (aumento permisible de 1/2) que también conserva la solución actual y denota el caso de infinitas soluciones en el tramo CD).