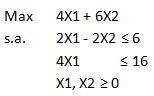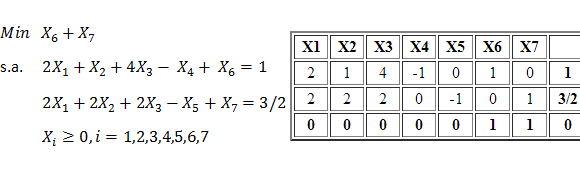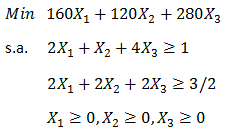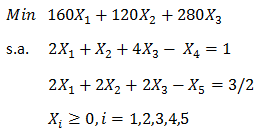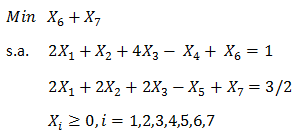En el siguiente artículo abordaremos a través de una discusión conceptual y ejemplos prácticos y sencillos las propiedades que establece el Teorema Fundamental de la Programación Lineal. Estas propiedades son indispensables tener en consideración al momento de la resolución algorítmica de este tipo de modelos de optimización matemática, destacando entre ellos el Método Simplex como así también la resolución de modelos lineales a través del Método Gráfico.
Teorema Fundamental de la Programación Lineal
Cada problema de Programación Lineal en su forma estándar cumple con las siguientes tres propiedades:
-
Propiedad 1: «Si el problema no tiene solución óptima entonces es no-acotado o infactible»
Notar que un problema lineal con dominio de soluciones factible no acotado puede (o no) admitir solución óptima, es decir, el hecho de enfrentar un modelo de estas características no determina a priori la presencia (o ausencia) de solución óptima.
En la aplicación del Método Simplex se detecta un problema no acotado sin solución óptima cuando al realizar el cálculo de la variable que deja la base, todos los elementos ykj de la columna j en la tabla, son negativos para j el índice de una variable no básica con costo reducido negativo. Por ejemplo consideremos el siguiente problema de Programación Lineal:
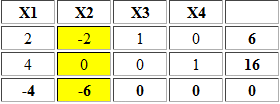
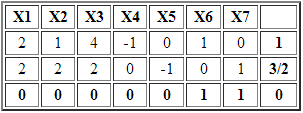
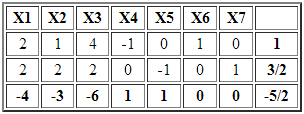
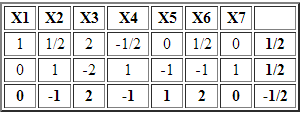
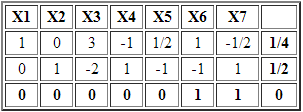
Luego de llevar a la forma estándar el modelo anterior, agregando X3 y X4 como variables de holgura para la restricción 1 y 2, respectivamente, se obtiene la siguiente tabla inicial.
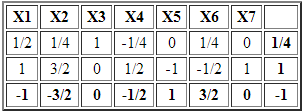
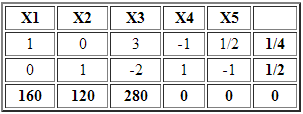
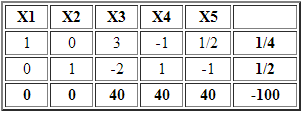
X2 es una variable no básica con costo reducido negativo y en consecuencia la incorporamos a la base. Sin embargo no es factible calcular el criterio de factibilidad o mínimo cuociente debido a que las entradas en la columna de X2 son negativas o cero. Lo anterior deja en evidencia que el problema es no acotado sin solución óptima.
Por otra parte un modelo lineal es infactible (dominio de soluciones factibles vacío y por tanto no admite solución) si el valor de la función objetivo al finalizar la Fase I del Método Simplex de 2 Fases es distinto a cero.
-
Propiedad 2: «Si tiene una solución factible, tiene una solución básica factible»
Una propiedad básica de los modelos de Programación Lineal es que en caso de admitir solución óptima, ésta se encontrará necesariamente en un vértice o tramo en la frontera del dominio de soluciones factibles.
En este contexto en la aplicación del Método Simplex como estrategia algorítmica de resolución, se busca proveer soluciones que cumplan con Ax=b (restricciones de la forma estándar) y x≥0, definiendo una solución básica factible (no necesariamente óptima).
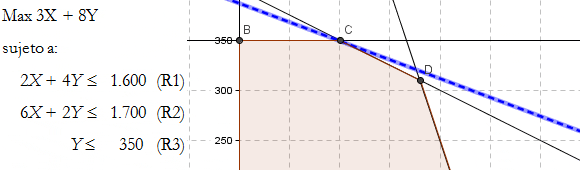
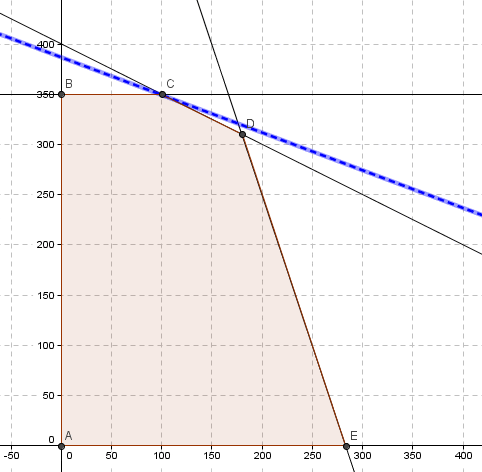
Por ejemplo en el siguiente gráfico que representa un modelo lineal en 2 variables se puede apreciar que los vértices A, B, C, D y E son soluciones básicas factibles.
-
Propiedad 3: «Si el problema tiene solución óptima, tiene una solución básica factible óptima»
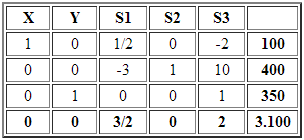
Siguiendo con el ejemplo anterior el vértice C no sólo es una solución básica factible sino también una solución básica factible óptima. Si todos los costos reducidos (de las variables no básicas: S1 y S3) son mayores o iguales que cero y estamos en presencia de una solución básica factible (X=100, S2=400, Y=350 todas ≥0), se cumple con el criterio de parada del Método Simplex y en consecuencia la actual solución básica factible es óptima.