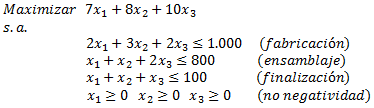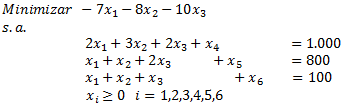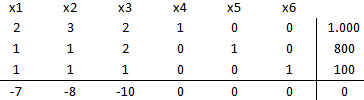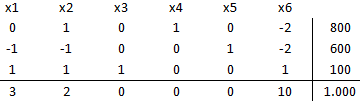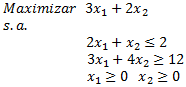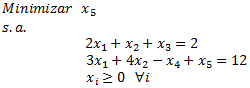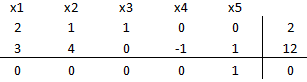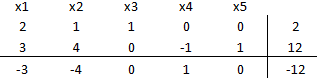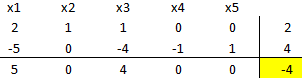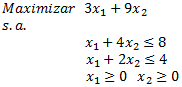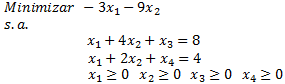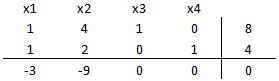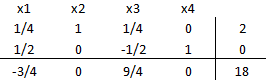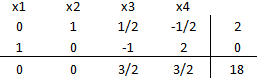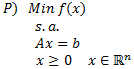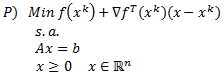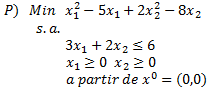método simplex Archivos - Página 3 de 7

Problema de Producción y Ensamblaje resuelto con el Método Simplex

El siguiente problema de Programación Lineal fue enviado por uno de nuestros lectores desde Puerto Rico. Consiste en determinar la política óptima de producción y ensamblaje de una empresa que se dedica a fabricar componentes para computadoras. A continuación los detalles de dicho problema el cual luego de su formulación (definición de las variables de decisión, función objetivo y restricciones) será resuelto a través del Método Simplex:

Problema de Producción y Ensamblaje

Una pequeña compañía fábrica tres componentes electrónicos de computadoras. Componente A requiere 2 horas de fabricación, 1 hora de ensamblaje y 1 hora de finalización; Componente B requiere 3 horas de fabricación, 1 hora de ensamblaje y 1 hora de finalización; y el Componente C requiere 2 horas de fabricación, 2 horas de ensamblaje y 1 hora de finalización. La compañía tiene a lo sumo 1.000 horas de labor en la fabricación, 800 horas de labor en el ensamblaje y 100 horas de finalización disponibles cada semana. Las ganancias de cada componente A, B y C, son $7, $8 y $10, respectivamente.

¿Cuántos componentes de cada tipo debe la compañía fabricar cada semana de manera que pueda maximizar sus ganancias? ¿Cuál es la ganancia máxima?. Resuelva el problema de Programación Lineal utilizando el Método Simplex.

Sea $x_{1}, x_{2}, x_{3}$ la cantidad de unidades a producir semanalmente del Componente A, B y C, respectivamente, un modelo de Programación Lineal que permite abordar el problema anterior es:

De modo de resolver el modelo a través del Método Simplex llevamos el mismo al formato estándar, agregando $x_{4}, x_{5}, x_{5}$ como variables de holgura de las restricciones 1, 2 y 3, respectivamente (fabricación, ensamblaje y finalización).

Lo que da origen a la siguiente tabla inicial del método:

Por el criterio del costo reducido más negativo ingresa a la base la variable $x_{3}$ . Luego calculamos el mínimo cuociente en dicha columna obteniendo: $Min \begin{Bmatrix}{\frac{1.000}{2}, \frac{800}{2}, \frac{100}{1}}\end{Bmatrix}=100$ , el pivote está en la fila 3 y en consecuencia $x_{6}$ deja la base. Se realiza entonces una iteración:

Notar que luego de una iteración las variables no básicas $x_{1}, x_{2}, x_{6}$ tienen costos reducidos mayores a cero, además las variables básicas cumplen con las condiciones de no negatividad, a saber, $x_{3}=100, x_{4}=800, x_{5}=600$ , lo que corresponde a una solución básica factible óptima. En consecuencia se propone producir exclusivamente 100 unidades del Componente C lo que reporta un valor óptimo (ganancia máxima) de $1.000.

Método de la Esquina Noroeste (Algoritmo de Transporte en Programación Lineal)

El Método de la Esquina Noroeste (o esquina superior izquierda) es una heurística que se aplica a una estructura especial de problemas de Programación Lineal llamada Modelo de Transporte, la cual permite asegurar que exista una solución básica factible inicial (no artificial). Otros métodos para la obtención de una solución básica de inicio son el Método de Costo Mínimo y Método de Aproximación de Vogel. En general, el Método de Vogel produce la mejor solución básica de inicio y el de la Esquina Noroeste la peor, sin embargo, el Método de la Esquina Noroeste implica el mínimo de cálculos.

El Método de la Esquina Noroeste comienza en la celda (ruta) correspondiente a la esquina noroeste, o superior izquierda, de la tabla (variable $x_{11}$ ). A continuación una descripción de los pasos:

Paso 1: Asignar todo lo posible a la celda seleccionada y ajustar las cantidades asociadas de oferta y demanda restando la cantidad asignada.

Paso 2: Salir de la fila o la columna cuando se alcance oferta o demanda cero, y tacharlo, para indicar que no se pueden hacer más asignaciones a esa fila o columna. Si una fila y una columna dan cero al mismo tiempo, tachar sólo uno (la fila o columna) y dejar una oferta (demanda) cero en la fila (columna) que no se tachó.

Paso 3: Si queda exactamente una fila o columna sin tachar, detenerse. En caso contrario, avanzar a la celda de la derecha si se acaba de tachar una columna, o a la de abajo si se tachó un reglón. Seguir con el Paso 1.

Método de la Esquina Noroeste

Para ilustrar la aplicación del Método de la Esquina Noroeste consideremos el siguiente problema balanceado de transporte que considera 3 silos productos (oferta) que satisfacen las necesidades de 4 molinos (demanda). El algoritmo de transporte se basa en la hipótesis que el modelo está balanceado, es decir, que la demanda total es igual a la oferta total (si el modelo no está balanceado siempre se podrá aumentar con una fuente ficticia o un destino ficticio para restaurar el equilibrio o balance).

Los costos unitarios de transporte desde el silo i al molino j $c_{ij}$ se representan en la esquina superior derecha de cada cuadro. Por ejemplo el costo unitario de enviar una unidad de producto desde el silo 1 al molino 1 es de $10. Adicionalmente los silos 1, 2 y 3 tienen capacidad u oferta de 15, 25 y 10 unidades, respectivamente. Por otra parte los molinos 1, 2, 3 y 4 tienen requerimientos o demanda de 5, 15, 15 y 15 unidades, respectivamente. El modelo esta balanceado (suma oferta = suma demanda = 50 unidades).

Al aplicar el Método de la Esquina Noroeste al ejemplo anterior se obtienen los siguientes resultados. Las flechas indican el orden en el que se generan las cantidades asignadas:

La cantidad asignada a la celda $x_{11}$ son 5 unidades, dado que si bien el silo 1 tiene capacidad de 15 unidades, el molino 1 sólo necesita (demanda) 5 unidades (no se realizan más asignaciones a la columna 1 correspondiente al molino 1).
A continuación nos movemos a la derecha y asignamos lo máximo posible (10 unidades remanentes) a la celda $x_{12}$ (con lo cual se completa la capacidad del silo 1 y en consecuencia no es posible seguir realizando asignaciones en la fila 1).
Luego asignamos 5 unidades a la celda $x_{22}$ lo cual es por cierto menor que la capacidad del silo 2 pero lo suficiente para satisfacer los requerimientos del molino 2 (ahora no es posible generar asignaciones adicionales a la columna 2).
Nos movemos a la derecha y se asignan 15 unidades del silo 2 al molino 3 ( $x_{23}=15$ ) lo que cubre inmediatamente los requerimientos del molino 3 (no es necesario asignar más en la columna 3).
Nuevamente nos movemos a la derecha y asignamos lo máximo posible (5 unidades que es la capacidad remanente del silo 2, es decir, $x_{24}=5$ ) con lo cual el silo 2 opera a máxima capacidad (ahora ya no es posible nuevas asignaciones en la fila 2).
Finalmente se asignan 10 unidades del silo 3 al molino 4 ( $x_{34}=10$ ) cubriendo la demanda de dicho molino (y la capacidad del correspondiente silo).

En consecuencia la solución básica factible inicial es: $x_{11}=5, x_{12}=10, x_{22}=5, x_{23}=15, x_{24}=5, x_{34}=10$ que reporta un costo del programa (valor en la función objetivo) de: Z=5(10)+10(2)+5(7)+15*(9)+5(20)+10*(18)=$520. Notar que si se implementa computacionalmente el problema anterior haciendo uso de Solver de Excel y utilizando como motor de resolución Simplex_LP se alcanza la siguiente solución óptima (celdas amarillas) con costo mínimo (valor óptimo) de $435.

Cómo detectar que un Problema de Programación Lineal es infactible con el Método Simplex de 2 Fases

Un problema infactible en Programación Lineal es una situación que se detecta cuando en la aplicación del Método Simplex de 2 Fases el valor óptimo del problema de la Fase 1 es distinto a cero (para continuar a la Fase 2 se requiere que el valor óptimo de la Fase 1 sea cero). Cabe recordar que un problema infactible es aquel cuyo dominio de soluciones factibles es vacío.

Consideremos el siguiente modelo de Programación Lineal en 2 variables que nos permitirá representar dicha situación:

Agregamos las siguientes variables al modelo para aplicar el Método Simplex de 2 Fases: $x_{3} (holgura), x_{4} (exceso), x_{5} (auxiliar)$ .

Definiendo el problema inicial de la Fase 1:

A continuación llevamos el costo reducido de la variable $x_{5}$ a cero, multiplicando por -1 la fila 2 y sumando ésta a la fila 3:

Para favorecer la rapidez de convergencia del método $x_{2}$ entra a la base. Luego calculamos el criterio del mínimo cuociente: $Min \begin{Bmatrix}{\frac{2}{1}, \frac{12}{4}}\end{Bmatrix}=2$ por tanto $x_{3}$ deja la base. Actualizamos la tabla:

Notar que todas las variables no básicas $x_{1}, x_{3}, x_{4}$ tienen costos reducidos mayores o iguales a cero. Adicionalmente las variables básicas $x_{2}, x_{5}$ cumplen con las condiciones de no negatividad. En consecuencia hemos finalizado la Fase 1 del Método Simplex de 2 Fases, sin embargo, el valor de la función objetivo es distinto de cero (en el ejemplo es -4) lo que determina que el problema es infactible.

La siguiente representación gráfica del problema anterior se puede realizar con Geogebra. El área achurada color rojo corresponde a la intersección de los conjuntos de factibilidad definido por la restricción 1 y las de no negatividad. Por otra parte el área achurada color azul es la intersección de los conjuntos de factibilidad definido por la restricción 2 y las de no negatividad. Luego resulta evidente que la intersección de dichos conjuntos (rojo y azul) es vacío, por tanto no existen valores que puedan adoptar las variables de decisión y satisfacer de forma simultanea todas las restricciones del problema.

Qué es una Solución Óptima Degenerada en Programación Lineal

En la aplicación del Método Simplex al hacer el cálculo del mínimo cuociente o condición de factibilidad, se puede romper un empate en la razón o cuociente mínimo en forma arbitraria. En este caso, al menos una variable básica será cero en la siguiente iteración, afirmándose en este caso que la nueva solución es degenerada. La implicancia práctica de dicha condición indica que el modelo tiene al menos una restricción redundante.

Solución Óptima Degenerada

Consideremos el siguiente modelo de Programación Lineal el cual resolveremos a través del Método Simplex y que de forma complementaria representaremos gráficamente con Geogebra:

Llevamos el problema anterior a su forma estándar de minimización, agregando $x_{3}$ y $x_{4}$ , como variables de holgura de las restricciones 1 y 2, respectivamente.

Que da origen a la siguiente tabla inicial del Método Simplex:

Para favorecer la rapidez de convergencia del algoritmo seleccionamos $x_{2}$ como la variable que ingresa a la base. A continuación calculamos el criterio de factibilidad (mínimo cuociente): $Min \begin{Bmatrix}{\frac{8}{4}, \frac{4}{2}}\end{Bmatrix}=2$ (al existir empate seleccionaremos arbitrariamente la variable $x_{3}$ como aquella que deja la base. Luego se actualiza la tabla:

Ahora $x_{1}$ ingresa a la base. El criterio de factibilidad determina que: $Min \begin{Bmatrix}{\frac{2}{1/4}, \frac{0}{1/2}}\end{Bmatrix}=0$ $x_{4}$ deja la base. Se realiza entonces una nueva iteración:

Se alcanza la solución óptima degenerada del problema lineal. Notar que $x_{1}=0, x_{2}=2, x_{3}=0, x_{4}=0, V(P)=18$ . Como éste es un problema bidimensional, la solución está sobredeterminada y una de las restricciones es redundante tal como se corrobora en la representación gráfica:

En la práctica conocer que algunos recursos (como los asociados a una restricción) son superfluos puede ser valioso durante la implementación de la solución. Desde el punto de vista teórico, la degeneración tiene dos implicaciones: se genera el fenómeno de ciclos o círculos (es posible que el Método Simplex repita una serie de iteraciones sin mejorar el valor de la función objetivo, tal como se observo en el ejemplo anterior e incluso eventualmente nunca terminar los cálculos); el segundo aspecto teórico surge al examinar las iteraciones 1 y 2. Las dos, aunque difieren en la clasificación de las variables básicas y no básicas, producen valores idénticos para todas las variables y el valor objetivo ( $x_{1}=0, x_{2}=2, x_{3}=0, x_{4}=0, V(P)=18$ ).

Ejemplo del Método de Frank Wolfe en Programación No Lineal

El método o algoritmo de Frank Wolfe fue propuesto en 1956 por Marguerite Frank y Philip Wolfe y se aplica a problemas de optimización matemática con una función objetivo no lineal convexa y cuyo dominio de soluciones factibles esta compuesto exclusivamente por restricciones lineales, es decir, es un conjunto convexo (en consecuencia el problema es convexo).

Consideremos el siguiente problema que asumiremos cumple con el formato anteriormente descrito:

Dada una aproximación $x^{k}$ a la solución óptima del problema, podemos resolver un problema más sencillo que aproxime al problema P), suponiendo $x^{k}$ factible.

O equivalentemente resolviendo el siguiente problema:

Que puede ser resuelto mediante el Método Simplex. Denotamos por $x_{PL}^{k}$ la solución óptima de $PL_{k}$ . El método contempla en seguida una minimización de un problema unidimensional que equivale a escoger un escalar $\alpha _{k}$ de modo que:

En seguida se define la siguiente aproximación al óptimo como:

Que equivale a definir $x^{k+1}$ como la solución óptima de f restringida al conjunto de puntos que determina al segmento que une $x^{k}$ con $x_{PL}^{k}$ .

Ejemplo: Aplicar el método de Frank Wolfe al siguiente problema no lineal restringido (convexo). Notar que la matriz hessiana o de segundas derivadas de la función objetivo es positiva definida.

Realizamos la primera iteración del método que da origen al siguiente problema de Programación Lineal:

La resolución es trivial y puede ser alcanzada de forma gráfica con Geogebra. La solución óptima es $x_{PL}^{0}=(0,3)$ según se aprecia a continuación:

Luego buscamos la solución para el problema unidimensional en términos del parámetro $\alpha$ :

Finalmente se obtiene $x^{1}=x^{0}+\frac{2}{3}(x_{PL}^{0}-x^{0})=(0,2)$ concluyendo una iteración del método de Frank Wolfe. Se propone al lector seguir las iteraciones a contar de este punto. Por ejemplo se puede verificar que $x_{PL}^{1}=(2,0)$ . (Hint: La solución óptima se alcanza en $(x_{1},x_{2})=(1,\frac{3}{2})$ .