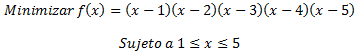A diferencia de la Programación Lineal donde sus distintas aplicaciones corresponden a problemas de optimización convexos (situación que facilita la resolución computacional), en Programación No Lineal no existen garantías a priori que permita garantizar que un modelo en particular será un problema convexo.
Es decir, una aplicación de Programación No Lineal puede ser un problema convexo o un problema no convexo.
En este artículo abordaremos a través de un ejemplo sencillo las dificultades prácticas y algorítmicas asociadas a la resolución de un modelo de Programación No Lineal no convexo.
Consideremos el siguiente modelo matemático no lineal con restricciones:
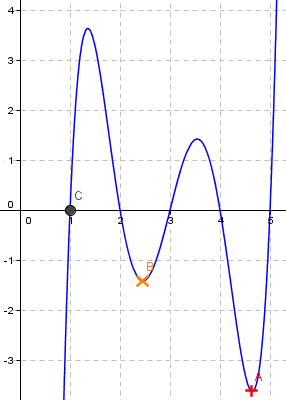
Una primera aproximación a su resolución consiste en graficar la función anterior utilizando Geogebra:
Se puede observar que la función es no convexa, constatándose adicionalmente la presencia de mínimos locales (por ejemplo los Puntos B y C) y mínimo global (Punto A).
En este sentido la expectativa que debiéramos tener al implementar este problema computacionalmente es obtener la solución óptima para un valor de x en el intervalo entre [4,5] (por simple inspección) lo que corresponde al Punto A de la gráfica anterior.
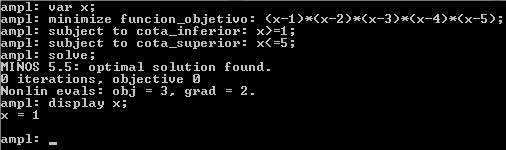
Una alternativa de resolución computacional para este problema es utilizar AMPL como lenguaje de programación matemática y MINOS 5.5 como solver de resolución. El código de la implementación y los resultados alcanzados se muestra a continuación:
La solución óptima encontrada por el algoritmo corresponde a x=1 (Punto C) lo que permite alcanzar un valor en la función objetivo igual a cero: f(1)=0. Claramente según nuestro gráfico esta solución corresponde sólo a un mínimo local aun cuando el programa sugiere que es el mínimo global del problema.
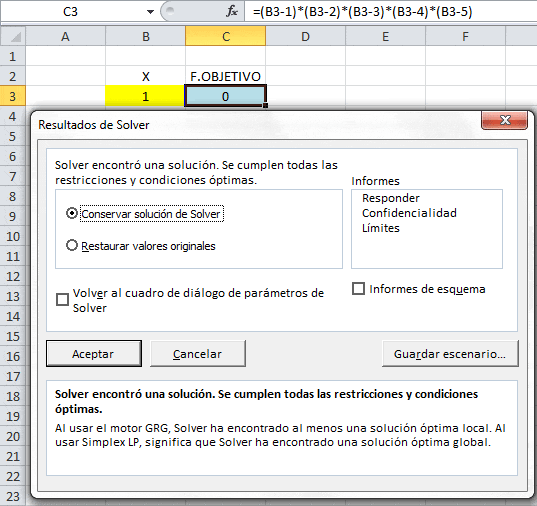
Otra alternativa de resolución consiste en la utilización de Solver. En primera instancia el algoritmo converge a la solución x=1 con f(1)=0.
Sin embargo, si manualmente editamos el valor de la celda color amarillo B3 (variable de decisión) a «2» y reoptimizamos con Solver se obtiene lo siguiente:
Se alcanza ahora una nueva solución con x=2,45608774 con f(2,45608774)=-1,41869663 lo que corresponde al Punto B de nuestro gráfico y que si bien corresponde a un mínimo local provee un valor menor en la función objetivo al ser comparado con el Punto C. En este contexto resulta razonable considerar el valor «4» para la celda cambiante como punto de partida para una nueva reoptimización:
Ahora obtenemos lo que correspondería al mínimo global del problema (Punto A) con solución óptima x=4,64443285 y valor óptimo f(4,64443285)=-3,63143221.
Finalmente hemos resuelto el problema con What’sBest! donde en el siguiente tutorial de nuestro canal de Youtube mostramos los detalles de la implementación:
Luego de reoptimizar sobre la solución local alcanzada en primera instancia se obtiene el mínimo global del problema (Punto A):
Conclusiones: Las principales dificultades enfrentadas al intentar resolver un modelo de Programación No Lineal no convexo es no tener la certeza si la solución obtenida a través de una herramienta computacional corresponde a un mínimo local o mínimo global.
Con las herramientas presentadas en este artículo fue necesario reoptimizar sobre soluciones obtenidas en primera instancia para encontrar la solución óptima del problema. Cabe destacar que en este ejemplo al disponer de una representación gráfica del problema sabíamos de antemano cuál era la solución del problema lo cual nos permitía contrastar los resultados computacionales. En este sentido claramente un modelo de mayor complejidad (por ejemplo, un mayor número de variables de decisión y/o restricciones) una aproximación intuitiva no tiene sentido práctico.
En este contexto una de las principales áreas actuales de desarrollo de la Investigación de Operaciones es proveer de métodos numéricos de resolución que permita abordar de forma eficiente la complejidad de esta categoría de problemas de optimización.