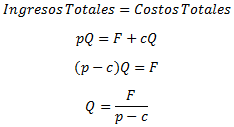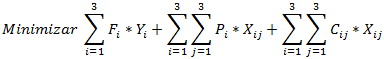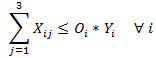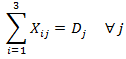producción Archivos - Página 2 de 4 - Gestión de Operaciones

Ejemplo del Cálculo del Punto de Equilibrio

En todo negocio un aspecto imprescindible consiste en evaluar la ganancia potencial de un producto o servicio, ya sea nuevo o existente. Se considera que los costos asociados a la producción de un producto o prestación de un servicio se puede dividir básicamente en 2 categorías: costos fijos (independientes del volumen de producción dentro de un rango de producción relevante) y costos variables (que varían directamente con el volumen de producción, asumiendo una relación lineal o proporcional). En este contexto el punto de equilibrio determina cuál debe ser el número de unidades vendidas que permite equiparar los ingresos totales con los costos totales, es decir, aquel volumen de ventas que evita pérdidas y ganancias.

Dado lo anterior queda de manifiesto la importancia de la evaluación del punto de equilibrio. El análisis se enfoca a responder preguntas del tipo:

¿Las ventas pronosticadas resultan ser suficientes para evitar pérdidas?
¿Cuánto debe bajar el costo variable unitario para alcanzar el punto de equilibrio, dadas las condiciones actuales de precios y proyecciones de ventas?
¿Cuál es el impacto del precio unitario en la obtención del punto de equilibrio?
¿Cuánto deben bajar los costos fijos para estar en una situación sin ganar o perder?

Sea $CT=F+cQ$ el costo total de producir un bien o prestar un servicio, donde $F$ es el costo fijo y $cQ$ los costos variables ( $c$ es el costo unitario y $Q$ la cantidad vendida). Adicionalmente sea $IT=pQ$ el ingreso total, donde $p$ es el precio unitario. El punto de equilibrio en términos de las unidades vendidas esta dado por:

Ejemplo Cálculo del Punto de Equilibrio

Una clínica esta evaluando un nuevo examen que reportará ingresos de $200 por paciente. El costo fijo anual será de $100.000 y los costos variables son de $100 por paciente. ¿Cuál es el punto de equilibrio para este servicio?.

Al evaluar en la fórmula anterior obtenemos lo siguiente:

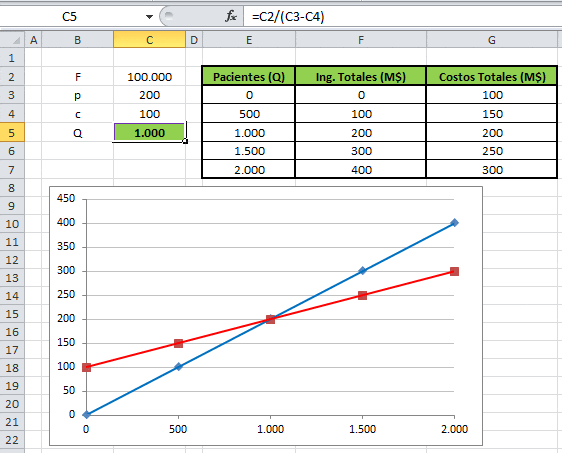
Es decir, si se realizan 1.000 exámenes (asumiendo un examen por paciente) los ingresos totales igualan a los costos totales, evitando tanto pérdidas como ganancias. De forma complementaria con la ayuda de Excel se puede evaluar de forma sencilla tanto los ingresos como costos totales para distintos niveles de actividad (en este caso número de exámenes o pacientes). La línea azul representa el ingreso total en miles de $ (eje vertical) para distintos valores de números de pacientes (eje horizontal). La línea roja representa el costo total donde resulta de particular interés observar que su valor es de $100 (mil) en el caso de cero pacientes (costo fijo).

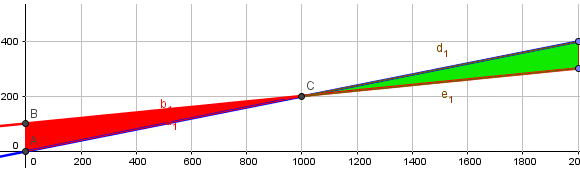
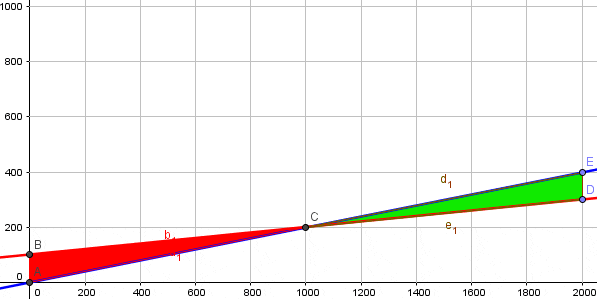
Una representación alternativa del ejemplo anterior hemos desarrollado con Geogebra, la cual se muestra a continuación. El área achurada de color rojo representa la pérdida, es decir, cuando el número de pacientes es menor al punto de equilibrio, por el contrario el área achurada de color verde representa la ganancia, en la cual se incurre cuando el nivel de pacientes supera el punto de equilibrio.

Problema de Explotación de Minas y Transporte de Carbón a Puertos

Es frecuente reconocer en los problemas de optimización que representan una estructura productiva, un componente de costo fijo asociado a la utilización de un recurso (dentro de un intervalo de producción relevante) y un costo variable que que asume proporcional al nivel de actividad que represente la unidad productiva (por ejemplo, lo que se refiere a costos de producción, costos de transporte en una red logística, entre otros). Por ejemplo, el Problema de Inclusión de Costos Fijos en Programación Entera representa una situación muy sencilla de lo anteriormente descrito.

En este contexto a continuación se presenta un problema de operación de minas de carbón que su simple utilización tiene asociado un costo fijo, además de incurrir en costos variables por concepto de producción y transporte a distintos puertos demandantes, que adicionalmente tienen requerimientos particulares sobre la calidad del producto recepcionado.

Problema de Explotación de Minas y Transporte

La compañía ABC puede explotar hasta tres minas de carbón y debe realizar envíos a tres puertos. El costo por tonelada de producción (en dólares), el costo fijo de operación en dólares (en caso de ser utilizada), los contenidos de una cierta clase de ceniza y de sulfuro por tonelada y las capacidades de producción (en toneladas de carbón) se resumen en la siguiente tabla:

Por su parte, las toneladas demandadas que deben ser enviadas a cada puerto, conjuntamente con los costos de transporte (en dólares por tonelada) se dan en la siguiente tabla:

Formule y resuelva un modelo de optimización que permita determinar la eventual operación de cada mina y sus niveles de producción, de modo de satisfacer los requerimientos de demanda y que las cantidades enviadas a cada puerto contenga a los más un 4,5% de ceniza y a lo más un 3% de sulfuro.

Variables de Decisión:

Parámetros:

Función Objetivo: Se desea minimizar los costos asociados a la explotación de las minas, el costo de producción del carbón y los costos de transporte del carbón enviado desde las minas a los puertos.

Restricciones:

Capacidad de Producción de las Minas: cada mina puede operar a su capacidad máxima de producción para abastecer los requerimientos de los distintos puertos en caso en que se decida realizar funciones de explotación en la misma.

Demanda de Carbón los Puertos: cada puerto debe recibir la cantidad de toneladas de carbón que demanda.

Máximo Porcentaje de Ceniza admitido por cada Puerto: cada puerto esta dispuesto a recibir como máximo un 4,5% de ceniza en los envíos de carbón que recibe desde las minas. En este caso se expresa dicha condición de forma general a través de parámetros.

Máximo Porcentaje de Sulfuro admitido por cada Puerto: similar al caso anterior pero estableciendo un límite máximo al porcentaje de sulfuro que admite cada puerto (en el ejemplo un 3%).

No Negatividad: las toneladas producidas en las minas y transportadas a los puertos naturalmente deben satisfacer las condiciones de no negatividad.

A continuación de presenta un extracto de la implementación computacional del modelo anterior haciendo uso de Solver de Excel junto a un tutorial de nuestro canal de Youtube con los detalles de la resolución:

Se puede observar que sólo se utilizan las minas 1 y 3. La mina 1 envía 35, 45 y 30 toneladas al Puerto 1, 2 y 3, respectivamente. En el caso de la mina 3, ésta envía 35, 35 y 30 toneladas a los Puertos 1, 2 y 3, respectivamente. La demanda en toneladas de carbón es satisfecha en los puertos y se respeta adicionalmente la capacidad máxima de producción de las minas. Adicionalmente se puede observar en color verde el porcentaje de ceniza o sulfuro (según sea el caso) que recibe cada puerto lo cual satisface las condiciones expuestas. Finalmente el valor óptimo, es decir, el costo mínimo asociado al plan de producción y transporte descrito es de 14.550 dólares.

¿Quieres tener el archivo Excel con la implementación computacional de este problema?

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Cálculo de la Capacidad de Producción en un Proceso Flexible con una Carta Gantt

En el artículo Cómo calcular la Capacidad y el Tiempo de Ciclo de un Proceso con una Carta Gantt discutimos cómo obtener estos importantes indicadores de procesos con el apoyo gráfico y conceptual que representa la utilización de una Carta Gantt. En dicho caso la resolución del problema se vio facilitada al asumir que los recursos asociados a las distintas actividades o tareas eran independientes entre sí. En este contexto se asume que el trabajador que participa de una etapa del proceso lo hace de forma exclusiva en dicha etapa sin colaborar en otras.

Por el contrario, calcular la capacidad y tiempo de ciclo de un proceso flexible, es decir, aquel donde los recursos pueden estar asociados a más de una actividad, impone un reto de mayor dificultad. Una aproximación intuitiva en este caso es construir una Carta Gantt que muestre el detalle del proceso de producción para luego deducir el tiempo promedio de ciclo y la capacidad. El siguiente ejemplo da cuenta de esta situación:

En un hospital hay dos doctores (Pedro y Francisca) y un enfermero (Diego) dedicados al control de niño sano. Para controlar a un niño se deben seguir los siguientes pasos:

Toma de Datos: Se deben tomar los datos del paciente e ingresarlos al computador. Se deben actualizar algunos campos, revisar los antecedentes e imprimir una ficha. Esto toma 5 minutos y solo lo puede hacer Diego.
Toma de Muestras: Se debe tomar la presión, peso y una muestra de sangre del paciente. Esto toma 5 minutos y lo puede hacer un doctor o un enfermero.
Consulta: Se debe examinar al paciente y completar la ficha. Esto toma 10 minutos y lo debe hacer un doctor.

Francisca propone organizar el trabajo de forma flexible. Es decir, en este nuevo esquema, Diego toma los datos, cualquiera de los tres podría tomar muestras, y ella o Pedro podrían atender consultas. Francisca opina que de esta forma podría aumentarse la utilización del staff en relación a la alternativa donde Diego toma los datos y las muestras y los doctores se dedican exclusivamente a las consultas.

Para evaluar lo propuesto anteriormente se sugiere confeccionar una Carta Gantt que permita determinar el mayor número de niños que es posible terminar de atender durante la primera hora de trabajo. ¿Cuál es la capacidad del proceso? ¿Cuál es el tiempo promedio de ciclo?.

La Carta Gantt para el proceso descrito anteriormente es la siguiente:

Se puede observar que el tiempo de flujo del primer paciente (niño) es de 20 minutos (cuya toma de muestra y consulta es atendida por Pedro, aun cuando sería indistinto que esto sea realizado por Francisca). El segundo niño termina su atención al cabo de 25 minutos desde iniciadas las actividades y el tercer niño sale del sistema 5 minutos más tarde que el segundo niño (y así sucesivamente continua el análisis).

¿Cómo determinamos el tiempo promedio de ciclo?. Para ello nos interesa identificar un patrón de tiempo que explique la salida de una nueva atención. Para este propósito enumeraremos los minutos en los cuales terminan las atenciones (consulta) para los distintos niños (1, 2, 3, 4,…, 13): 20, 25, 30, 40, 45, 50, 60, 65, 70, 80, 85, 90, 100. Luego se evidencia un patrón en dicho comportamiento: el segundo niño termina 5 minutos más tarde que el primero y el tercer niño 5 minutos más tarde que el segundo, no obstante el cuarto niño se desocupa 10 minutos más tarde que el tercero (y así sucesivamente). En consecuencia se espera que en el largo plazo en un intervalo de 20 minutos se terminen de atender 3 niños (trabajando a máxima capacidad) por lo cual el tiempo promedio de ciclo tiende a 20[min]/3[niños]=6,666[min/niño].

Notar que esta situación resulta evidente cuando el número de pacientes tiende a un número grande (en teoría infinito) donde el tiempo promedio de ciclo va convergiendo a 6,666[min/niño]. El siguiente gráfico es una forma alternativa de representar la información de la tabla anterior donde se ha incorporado una linea de color rojo punteada que cruza el eje vertical (tiempo promedio de ciclo en [min/niño]) en 6,666.

¿Cuál es la capacidad máxima de producción?. Si el tiempo promedio de ciclo es de 6,666[min/niño] entonces la capacidad de producción es 1/6,666[niños/min]*60[min/hora]=9[niños/hora]. Notar que este resultado no contradice el hecho que durante la primera hora de trabajo sólo se han terminado de atender 7 niños.

Cálculo del Tiempo de Ciclo, Capacidad de Producción y Tiempo de Flujo de una Línea de Ensamble

Calcular los indicadores básicos de desempeño de un proceso productivo como lo es el tiempo promedio de ciclo, la capacidad máxima de producción y el tiempo de flujo de una unidad de producto en un proceso con actividades que se realizan en forma simultanea, puede resultar ser un trabajo más complejo en comparación a un proceso que sólo considera un conjunto de actividades que se desarrolla de forma secuencial. En este contexto se presenta un ejemplo de una empresa construcción de robots que trabaja con 3 lineas de ensamble que arman el Software, Hardware y Piezas de Conexión respectivamente, para luego ser unidas en una última linea de 3 tareas (I, J y K). El siguiente diagrama muestra las tareas necesarias para la construcción de producto final y las capacidades de cada tarea medidas en [u/hr].

A continuación se presentan algunas preguntas típicas del análisis cuantitativo de procesos que nos ayudarán a comprender de mejor forma el cálculo de los indicadores anteriormente individualizados.

1. Analizar el proceso indicando el tiempo de flujo del proceso, el tiempo de ciclo promedio, la tarea que es cuello de botella y la capacidad total del proceso.

El tiempo de flujo es la suma de la linea más larga junto con la linea de producción común, es decir, 19,3[min] + 11,6[min] = 30,9[min] (aproximado). Notar que esto implica que ningún producto final podrá ser terminado en un tiempo menor a 30,9[min], esto es, el tiempo que pasa desde que se inicia su procesamiento hasta que termina su ejecución en la etapa K.

Adicionalmente las capacidades de las actividades individuales en $[u/hr]$ han sido transformadas a sus tiempos de ciclo asociados, por ejemplo, si la actividad A tiene una capacidad de $15[u/hr]$ esto implica que su tiempo de ciclo es $4[min/u]$ (también sería válido decir que el tiempo de ciclo es $\frac{1}{15}[hr/u]$ ). Finalmente es sencillo notar que el cuello de botella son las tareas B y D, siendo la capacidad del sistema de $12[u/hr]$ .

2. Si pudiera agregar alguna tarea en paralelo (sin importar qué tarea sea), ¿Cuál sería? ¿Cuál es el nuevo cuello de botella?.

Si se pudiera agregar otra actividad naturalmente la tendríamos que agregar al cuello de botella, en este caso a las actividades B o D. Con esto el tiempo de flujo no cambia. El siguiente diagrama muestra el caso de incorporar una actividad D adicional:

La capacidad del proceso se mantiene en $12[u/hr]$ debido a que se conserva el cuello de botella de las actividades B. Ahora si se pudiera al diagrama anterior agregar una actividad B adicional en paralelo, entonces la capacidad del proceso estaría dada por las actividades C y J ( $13[u/hr]$ ).

Informe de Confidencialidad de Celdas de Variables y Restricciones de Solver

El siguiente problema tiene por objetivo mostrar la interpretación del Informe de Confidencialidad (o Informe de Sensibilidad) de Solver de Excel en los distintos escenarios que de éste se pueden considerar. Una empresa fabrica 3 productos (A, B y C) y desea planificar la producción semanal de cada uno de estos productos. Para ello dispone de 200 horas semanales en el departamento de corte, 350 horas semanales en el departamento de ensamblaje y 250 horas semanales en el departamento de terminado. Cada producto utiliza una determinada cantidad de horas en estos departamentos según lo muestran los parámetros en el lado izquierdo de las respectivas restricciones. Adicionalmente la empresa ha adquirido contratos con clientes que compran el producto B y C para producir al menos 50 y 30 unidades semanales, respectivamente. Finalmente según el departamento de ventas se ha estimado que la demanda máxima semanal para los productos A, B y C son 60, 120 y 80 unidades respectivamente.

Un modelo de Programación Lineal para la situación anterior es:

Luego de implementar en Solver de Excel el modelo anterior se obtiene el siguiente Informe de Confidencialidad (Informe de Sensibilidad):

1. ¿Cuánto estaría dispuesto a pagar para cancelar el contrato que obliga a producir al menos 30 unidades de C?

El Precio Sombra de la restricción de contrato del producto C es de -2 y su disminución permisible es de 30 unidades. Por tanto podemos utilizar el precio sombra para predecir el cambio en el valor óptimo ante la eliminación de este contrato (que sería equivalente a reemplazar $C\geq 30$ por $C\geq 0$ ). El valor óptimo en consecuencia aumentaría en -2*(0-30)=$60 que determina la máxima disposición a pagar para eliminar este contrato.

2. Suponga que se elimina el contrato que obliga producir al menos 50 unidades de B. ¿Cuál es el impacto en el impacto en el valor óptimo?

El Precio Sombra de la restricción de contrato del producto B es de -19 y su disminución permisible es de 10 unidades. Esto determina que reemplazar $B\geq 50$ por $B\geq 0$ no llevaría la producción de B a cero sino que sólo disminuiría a 40 unidades. Por tanto al eliminar este contrato el valor óptimo aumentaría en -19*(40-50)=$190 que determina la máxima disposición a pagar para eliminar este contrato.

3. Suponga que la empresa tiene $100 para invertir en capacidad. El costo de una hora extra de capacidad en los departamentos de Corte, Ensamblaje y Terminación es de $7, $5, y $6 respectivamente. ¿Cómo invertiría los fondos?. Asuma que sólo puede invertir en una de las 3 alternativas.

No tiene sentido destinar fondos adicionales para contratar horas extraordinarias en los departamentos de ensamblaje y terminado dado que en la actual solución óptima éstas restricciones no se encuentran activas y por tanto existen horas ociosas en dichos departamentos (70 y 80 horas semanales, respectivamente).

Por el contrario el departamento de corte se encuentra operando a máxima capacidad y dispone de un precio sombra de $9 que es mayor al costo de la hora extra de $7, por lo tanto conviene comprar capacidad adicional.

Con un presupuesto de $100 se pueden adquirir 14,2857 horas adicionales en el departamento de corte ($100/7) lo cual está dentro del aumento permisible para el precio sombra (23,3 horas) por tanto se destina la totalidad del presupuesto para dicho propósito.

4. ¿Cuál es el rango de variación para el coeficiente asociado a la variable B en la función objetivo que conserva la actual solución óptima?

Notar que la solución óptima actual es A=20, B=50, C=30. Adicionalmente el valor actual del parámetro en la función objetivo que pondera la variable B es 8, con un aumento permisible de 19 y una reducción permisible de 1E+30 (infinito). Es decir, el intervalo de variación para el parámetro que conserva la solución óptima es ]-1E+30,27]. La cota inferior del intervalo anterior cobra sentido al considerar la restricción de Contrato de B, que, independiente del beneficio (o pérdida) que reporte dicho producto al plan de producción, se debe fabricar de todos modos.