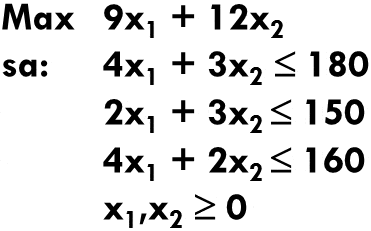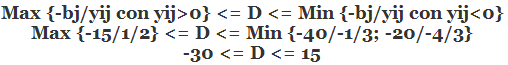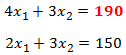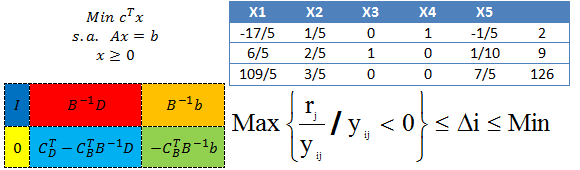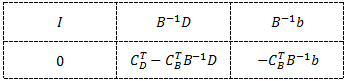restricción Archivos - Gestión de Operaciones

Cálculo del Intervalo de Variación del Lado Derecho que conserva la Base Óptima

Una vez concluidas las iteraciones del Método Simplex y en el caso de alcanzar una solución básica factible óptima, puede resultar de interés determinar un intervalo de variación para un parámetro del vector de los lados derechos de las restricciones que permita conservar la geometría del problema. Esto implica que se conservan las restricciones activas originales en el nuevo escenario (es decir, se mantiene la base óptima) que se genera a partir de la modificación (individual) de un parámetro o coeficiente del lado derecho. Para ilustrar el resultado anterior consideremos el siguiente modelo de Programación Lineal.

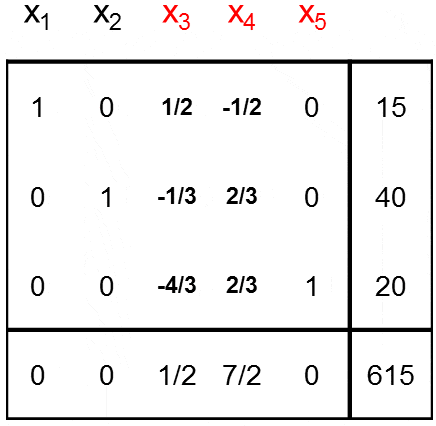
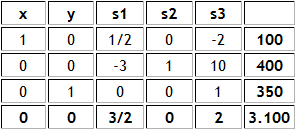
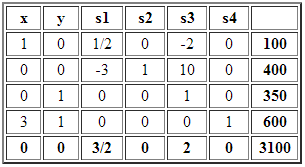
Luego de llevar a la forma estándar el modelo anterior agregando $x_{3}$ , $x_{4}$ y $x_{5}$ como las variables de holgura de las restricciones 1, 2 y 3, respectivamente, y aplicar las iteraciones necesarias del Método Simplex, se alcanza la siguiente tabla final (óptima):

La solución óptima es $x_{1}=15$ y $x_{2}=40$ con valor óptimo $V(P)=615$ . El valor de las variables de holgura en el óptimo $x_{3}$ , $x_{4}$ y $x_{5}$ es 0, 0 y 20, respectivamente. Luego se puede concluir que la solución óptima del problema se alcanza con las restricciones 1 y 2 activas (notar que sus respectivas holguras con variables no básicas en el óptimo) y la base actual esta conformada por las variables $x_{1}$ , $x_{2}$ y $x_{5}$ .

Sabemos adicionalmente que, por ejemplo, el costo reducido de la variable de holgura $x_{3}$ representa el precio sombra asociado a la primera restricción ( $\pi_{1}=1/2$ ). No obstante desconocemos en qué intervalo puede variar el parámetro del lado derecho de la restricción 1 (actualmente $b_{1}=180$ ) de modo que se conserve la base óptima y por tanto nos permita hacer un correcto uso de la información del precio sombra.

Para ello se propone la siguiente fórmula que permite encontrar el intervalo de variación para un lado derecho que conserva la base óptima:

Max {-bj/yij con yij>0} <= D <= Min {-bj/yij con yij<0}

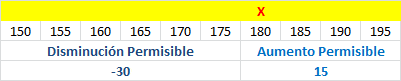
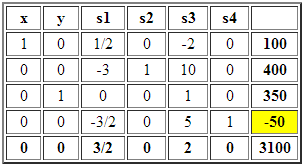
Por ejemplo determinemos el intervalo para el parámetro $b_{1}$ :

En consecuencia $b_{1}$ puede disminuir en 30 unidades y aumentar en 15 unidades y se conserva la base óptima. Es decir, si $b_{1}\epsilon [150,195]$ se mantiene la base óptima.

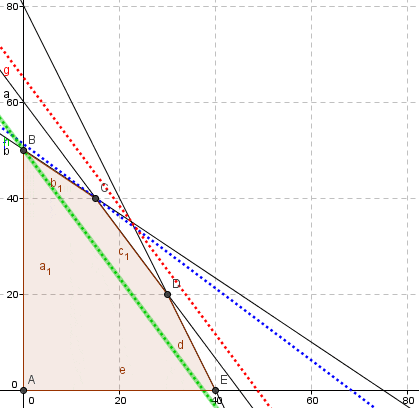
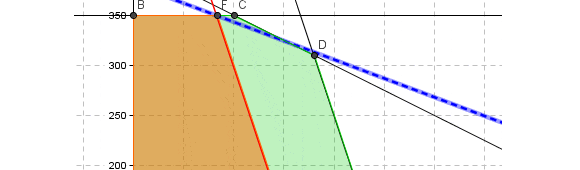
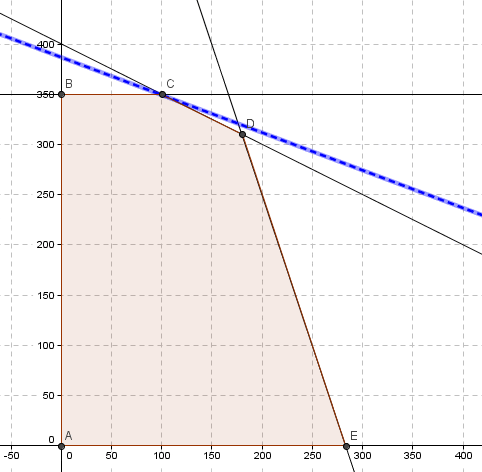
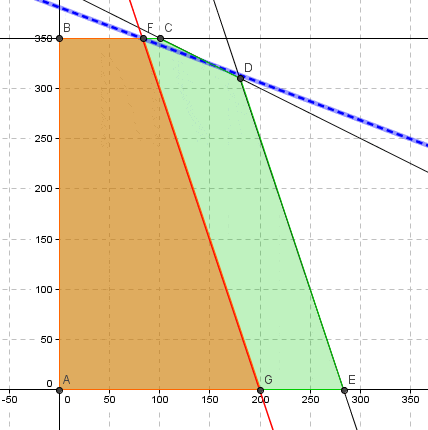
El resultado anterior se puede corroborar gráficamente. La solución óptima se encuentra en el vértice C donde las restricciones 1 y 2 son activas (notar la curva de nivel que pasa por el vértice óptimo es la línea punteada de color azul). Si para el lado derecho de la restricción 1 consideramos $b_{1}=150$ se obtiene la línea de color verde y para $b_{1}=195$ la línea de color rojo. En estos casos si bien se modifica el dominio de soluciones factibles, la solución óptima conserva las actuales restricciones activas (y por ende cuando $b_{1}$ adopta un valor fuera de este intervalo cambia la geometría del problema o base óptima).

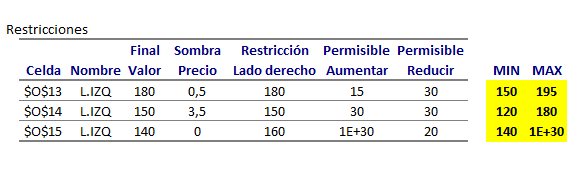
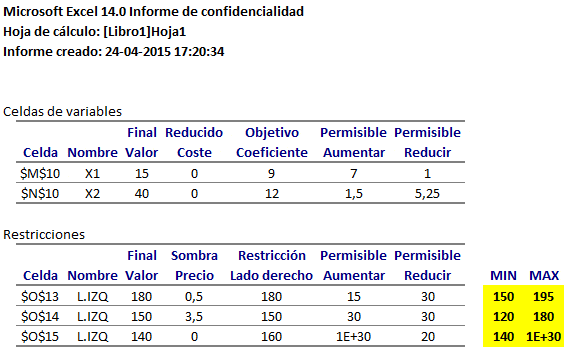
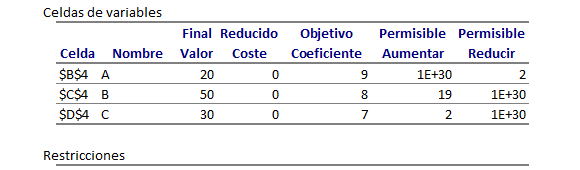
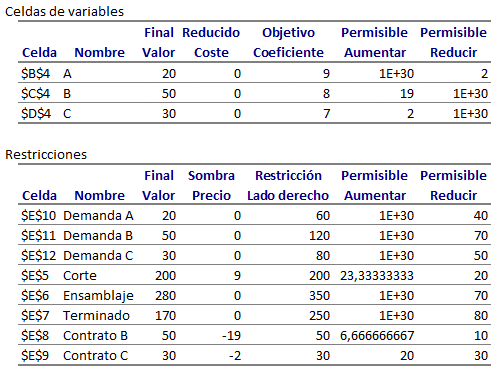
Esto es consistente con el Informe de Confidencialidad de Solver. En particular el reporte de restricciones donde se aprecia el aumento y reducción permisible que conserva la actual base óptima:

Por ejemplo, ¿cuál es el nuevo valor óptimo si el lado derecho de la restricción 1 ahora es $b_{1}=190$ ?. Como $b_{1}=190\epsilon[150,195]$ , entonces $V(P)=615+\Delta b_{1}\pi _{1}=615+(190-180)*(1/2)=620$ . ¿Cuál es la nueva solución óptima?. Como sabemos que se conservan las restricciones activas en el óptimo para la variación propuesta, la solución óptima del nuevo escenario se obtiene simplemente resolviendo el siguiente sistema de ecuaciones (notar que la restricción 1 y 2 se conservan activas):

De donde $x_{1}=20$ y $x_{2}=110/3$ , que al evaluar en la función objetivo se obtiene: $V(P)=9*(20)+12*(110/3)=620$ corroborando el resultado anterior. Dejamos al lector el desafío de aplicar los conceptos presentados en este articulo para encontrar un intervalo para $b_{2}$ y $b_{3}$ que conserve la base óptima.

Informe de Confidencialidad de Celdas de Variables y Restricciones de Solver

El siguiente problema tiene por objetivo mostrar la interpretación del Informe de Confidencialidad (o Informe de Sensibilidad) de Solver de Excel en los distintos escenarios que de éste se pueden considerar. Una empresa fabrica 3 productos (A, B y C) y desea planificar la producción semanal de cada uno de estos productos. Para ello dispone de 200 horas semanales en el departamento de corte, 350 horas semanales en el departamento de ensamblaje y 250 horas semanales en el departamento de terminado. Cada producto utiliza una determinada cantidad de horas en estos departamentos según lo muestran los parámetros en el lado izquierdo de las respectivas restricciones. Adicionalmente la empresa ha adquirido contratos con clientes que compran el producto B y C para producir al menos 50 y 30 unidades semanales, respectivamente. Finalmente según el departamento de ventas se ha estimado que la demanda máxima semanal para los productos A, B y C son 60, 120 y 80 unidades respectivamente.

Un modelo de Programación Lineal para la situación anterior es:

Luego de implementar en Solver de Excel el modelo anterior se obtiene el siguiente Informe de Confidencialidad (Informe de Sensibilidad):

1. ¿Cuánto estaría dispuesto a pagar para cancelar el contrato que obliga a producir al menos 30 unidades de C?

El Precio Sombra de la restricción de contrato del producto C es de -2 y su disminución permisible es de 30 unidades. Por tanto podemos utilizar el precio sombra para predecir el cambio en el valor óptimo ante la eliminación de este contrato (que sería equivalente a reemplazar $C\geq 30$ por $C\geq 0$ ). El valor óptimo en consecuencia aumentaría en -2*(0-30)=$60 que determina la máxima disposición a pagar para eliminar este contrato.

2. Suponga que se elimina el contrato que obliga producir al menos 50 unidades de B. ¿Cuál es el impacto en el impacto en el valor óptimo?

El Precio Sombra de la restricción de contrato del producto B es de -19 y su disminución permisible es de 10 unidades. Esto determina que reemplazar $B\geq 50$ por $B\geq 0$ no llevaría la producción de B a cero sino que sólo disminuiría a 40 unidades. Por tanto al eliminar este contrato el valor óptimo aumentaría en -19*(40-50)=$190 que determina la máxima disposición a pagar para eliminar este contrato.

3. Suponga que la empresa tiene $100 para invertir en capacidad. El costo de una hora extra de capacidad en los departamentos de Corte, Ensamblaje y Terminación es de $7, $5, y $6 respectivamente. ¿Cómo invertiría los fondos?. Asuma que sólo puede invertir en una de las 3 alternativas.

No tiene sentido destinar fondos adicionales para contratar horas extraordinarias en los departamentos de ensamblaje y terminado dado que en la actual solución óptima éstas restricciones no se encuentran activas y por tanto existen horas ociosas en dichos departamentos (70 y 80 horas semanales, respectivamente).

Por el contrario el departamento de corte se encuentra operando a máxima capacidad y dispone de un precio sombra de $9 que es mayor al costo de la hora extra de $7, por lo tanto conviene comprar capacidad adicional.

Con un presupuesto de $100 se pueden adquirir 14,2857 horas adicionales en el departamento de corte ($100/7) lo cual está dentro del aumento permisible para el precio sombra (23,3 horas) por tanto se destina la totalidad del presupuesto para dicho propósito.

4. ¿Cuál es el rango de variación para el coeficiente asociado a la variable B en la función objetivo que conserva la actual solución óptima?

Notar que la solución óptima actual es A=20, B=50, C=30. Adicionalmente el valor actual del parámetro en la función objetivo que pondera la variable B es 8, con un aumento permisible de 19 y una reducción permisible de 1E+30 (infinito). Es decir, el intervalo de variación para el parámetro que conserva la solución óptima es ]-1E+30,27]. La cota inferior del intervalo anterior cobra sentido al considerar la restricción de Contrato de B, que, independiente del beneficio (o pérdida) que reporte dicho producto al plan de producción, se debe fabricar de todos modos.

Análisis de Sensibilidad en Programación Lineal utilizando la Tabla Final del Método Simplex

Un supuesto básico asociado a la Programación Lineal es que los parámetros o constantes son valores conocidos con exactitud al momento de resolver el modelo de optimización. Este supuesto de asumir que no existe incertidumbre claramente implica una simplificación en el modelamiento de problemas de naturaleza real y es conocido como el supuesto de modelo determinista.

La optimización también permite incorporar explícitamente la incertidumbre en los parámetros en el modelamiento, asumiendo que la totalidad o un conjunto de éstos se distribuyen aleatoriamente, lo cual se puede representar a través de una función de probabilidad conocida o una distribución empírica que modela distintos escenarios para los parámetros, asociando una probabilidad de ocurrencia en cada caso. Esta categoría de modelos de optimización (por cierto más complejos en comparación al caso determinista) se llaman modelos estocásticos, los cuales en rara oportunidad se analizan en cursos introductorios de Investigación de Operaciones, de modo que forman parte del programa de estudios en cursos de Magíster y Doctorado asociado al área de optimización matemática.

En relación a lo anterior, si bien un modelo determinista considera valores fijos para los parámetros, aún podemos analizar los cambios en los resultados del modelo (solución óptima y valor óptimo principalmente) en comparación a lo obtenido en una instancia de resolución original o escenario base. Esto se conoce como análisis de sensibilidad o análisis postoptimal.

Recordemos que la estructura de la tabla final del Método Simplex se puede representar de la siguiente forma:

Donde:

I: Matriz Identidad (Diagonal de «1»)
0: Vector de costos reducidos asociados a las variables básicas
B: Matriz de variables básicas
D: Matriz de variables no básicas
b: Vector de «lado derecho»
Cb: Coeficientes en la función objetivo asociados a las variables básicas
Cd: Coeficientes en la función objetivo asociados a las variables no básicas

A continuación presentamos los Análisis de Sensibilidad más recurrentes asociados a los modelos de Programación Lineal y utilizando como fuente de información la tabla final del Método Simplex. El siguiente es un listado de los artículos que hemos desarrollado para cada uno de estos temas los cuales te recomendamos visitar:

Incorporar Nueva Restricción (Análisis Postoptimal Programación Lineal)

Una vez resuelto un modelo de Programación Lineal puede resultar de interés si la actual solución óptima y valor óptimo se conservaran si se decide incorporar una nueva restricción al problema. Esta restricción generalmente representa una condición que en primera instancia se omite de forma voluntaria para dar una mayor flexibilidad a la resolución del modelo original o alternativamente su no inclusión en el modelo original puede también deberse a una simple omisión (involuntaria).

Consideremos el siguiente modelo de Programación Lineal que hemos resuelto en un artículo previo a través del Método Simplex:

La tabla final óptima que considera las variables s1, s2 y s3 como las respectivas holguras de las restricciones del problema es:

Por ejemplo, consideremos que se desea incorporar una nueva restricción definida por la siguiente expresión: 3X+Y<=600. ¿Cambia la actual solución óptima y valor óptimo?.

Para responder a lo anterior se recomienda evaluar la actual solución óptima en la nueva restricción; si ésta se cumple entonces el modelo conserva su solución óptima y valor óptimo; en caso contrario la solución óptima actual será infactible y se debe incorporar esta situación en el modelo original para encontrar la nueva solución del mismo. Notar que también puede suceder que al agregar una nueva restricción que no satisface la solución actual el problema podría resultar ser infactible al tener un dominio de soluciones factibles vacío.

En nuestro ejemplo al evaluar obtenemos: 3(100)+(350)<=600, es decir, la solución óptima actual es infactible al incorporar esta nueva restricción.

Para incorporar esta modificación en la tabla final del Método Simplex agregamos una nueva fila y una nueva columna asociada a una variable s4>=0 que será la holgura de la nueva restricción. La tabla queda de la siguiente forma:

Las variables básicas del problema original son x, s2 e y, respectivamente. Al incorporar la nueva restricción (fila) tanto x como y pierden la estructura de la identidad característica de las variables básicas. Por ello para formar la base podemos realizar operaciones fila multiplicando por -3 la fila 1 y sumando ésta a la fila 4. Posteriormente multiplicar por -1 la fila 3 y sumar a la fila 4:

Ahora las variables básicas son x, s2, y, s4 (enumeradas en el orden en el cual aparecen en la identidad), sin embargo, la variable s4 toma un valor de -50 lo cual no corresponde a una solución básica factible.

¿Cómo continuar con las iteraciones?. Utilizando el Método Simplex Dual se recomienda corroborar que la nueva solución óptima corresponde a x=250/3 e y=350.

Adicionalmente podemos utilizar un enfoque de Resolución Gráfica para el problema anterior. El siguiente gráfico representa la resolución del escenario inicial donde la solución básica factible óptima se alcanza en el vértice C con x=100 e y=350.

Al incorporar la nueva restricción (recta color rojo) el dominio de soluciones factibles se ve reducido, donde ahora ya no son factibles los puntos en el polígono con área achurada color verde (donde se puede verificar que el vértice C es infactible).

Si se resuelve gráficamente sobre el nuevo dominio (área achurada color naranjo) las curvas de nivel de la función objetivo (recta punteada color azul) pasa por última vez en el vértice F donde x=250/3 e y=350 como solución óptima del nuevo problema.