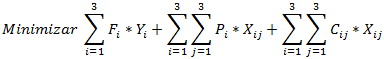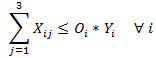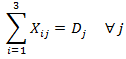Es frecuente reconocer en los problemas de optimización que representan una estructura productiva, un componente de costo fijo asociado a la utilización de un recurso (dentro de un intervalo de producción relevante) y un costo variable que que asume proporcional al nivel de actividad que represente la unidad productiva (por ejemplo, lo que se refiere a costos de producción, costos de transporte en una red logística, entre otros). Por ejemplo, el Problema de Inclusión de Costos Fijos en Programación Entera representa una situación muy sencilla de lo anteriormente descrito.
En este contexto a continuación se presenta un problema de operación de minas de carbón que su simple utilización tiene asociado un costo fijo, además de incurrir en costos variables por concepto de producción y transporte a distintos puertos demandantes, que adicionalmente tienen requerimientos particulares sobre la calidad del producto recepcionado.
Problema de Explotación de Minas y Transporte
La compañía ABC puede explotar hasta tres minas de carbón y debe realizar envíos a tres puertos. El costo por tonelada de producción (en dólares), el costo fijo de operación en dólares (en caso de ser utilizada), los contenidos de una cierta clase de ceniza y de sulfuro por tonelada y las capacidades de producción (en toneladas de carbón) se resumen en la siguiente tabla:
Por su parte, las toneladas demandadas que deben ser enviadas a cada puerto, conjuntamente con los costos de transporte (en dólares por tonelada) se dan en la siguiente tabla:
Formule y resuelva un modelo de optimización que permita determinar la eventual operación de cada mina y sus niveles de producción, de modo de satisfacer los requerimientos de demanda y que las cantidades enviadas a cada puerto contenga a los más un 4,5% de ceniza y a lo más un 3% de sulfuro.
Variables de Decisión:
Parámetros:
Función Objetivo: Se desea minimizar los costos asociados a la explotación de las minas, el costo de producción del carbón y los costos de transporte del carbón enviado desde las minas a los puertos.
Restricciones:
Capacidad de Producción de las Minas: cada mina puede operar a su capacidad máxima de producción para abastecer los requerimientos de los distintos puertos en caso en que se decida realizar funciones de explotación en la misma.
Demanda de Carbón los Puertos: cada puerto debe recibir la cantidad de toneladas de carbón que demanda.
Máximo Porcentaje de Ceniza admitido por cada Puerto: cada puerto esta dispuesto a recibir como máximo un 4,5% de ceniza en los envíos de carbón que recibe desde las minas. En este caso se expresa dicha condición de forma general a través de parámetros.
Máximo Porcentaje de Sulfuro admitido por cada Puerto: similar al caso anterior pero estableciendo un límite máximo al porcentaje de sulfuro que admite cada puerto (en el ejemplo un 3%).
No Negatividad: las toneladas producidas en las minas y transportadas a los puertos naturalmente deben satisfacer las condiciones de no negatividad.
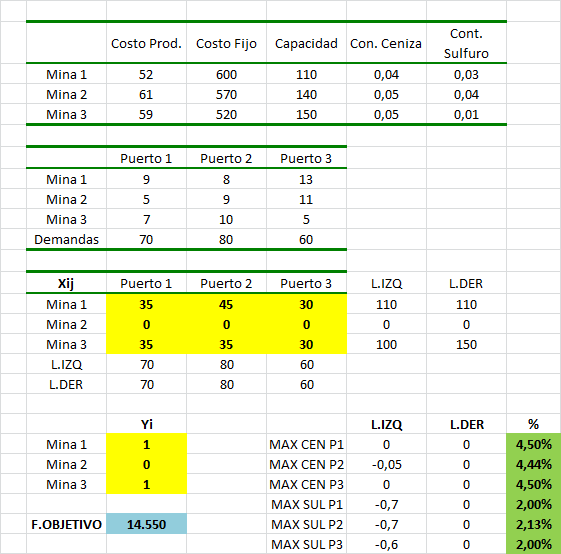
A continuación de presenta un extracto de la implementación computacional del modelo anterior haciendo uso de Solver de Excel junto a un tutorial de nuestro canal de Youtube con los detalles de la resolución:
Se puede observar que sólo se utilizan las minas 1 y 3. La mina 1 envía 35, 45 y 30 toneladas al Puerto 1, 2 y 3, respectivamente. En el caso de la mina 3, ésta envía 35, 35 y 30 toneladas a los Puertos 1, 2 y 3, respectivamente. La demanda en toneladas de carbón es satisfecha en los puertos y se respeta adicionalmente la capacidad máxima de producción de las minas. Adicionalmente se puede observar en color verde el porcentaje de ceniza o sulfuro (según sea el caso) que recibe cada puerto lo cual satisface las condiciones expuestas. Finalmente el valor óptimo, es decir, el costo mínimo asociado al plan de producción y transporte descrito es de 14.550 dólares.
¿Quieres tener el archivo Excel con la implementación computacional de este problema?
[sociallocker]
MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO
[/sociallocker]