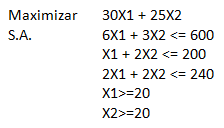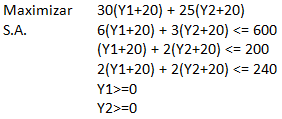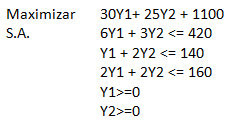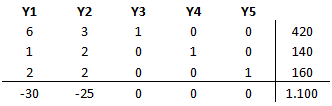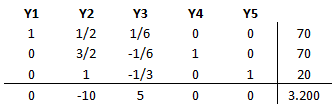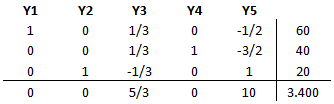Cuando se desea resolver un modelo de Programación Lineal es importante tener en cuenta que generalmente se dispone de varias alternativas las cuales difieren en dificultad y por tanto es necesario evaluar cada una en su mérito para luego decidir qué estrategia algorítmica utilizar.
Este concepto es válido tanto para la resolución de pequeños modelos de optimización lineales como los que usualmente se consideran para fines académicos, como también para modelos de mayor tamaño, donde seleccionar una estrategia adecuada favorece los tiempos y confiabilidad de la resolución computacional.
A continuación presentaremos un problema de Programación Lineal en 2 variables que resulta de interés su resolución:
Notar que existen distintas estrategias que nos permiten abordar el problema anterior. Por ejemplo, lo podríamos resolver gráficamente (Método Gráfico en Programación Lineal) o utilizar el Método Simplex de 2 Fases, agregando variables de holgura para las restricciones 1, 2 y 3 y variables de exceso y auxiliares para las restricciones 4 y 5. También por cierto se podría definir el Problema Dual del ejemplo anterior y luego intentar su resolución, lo que a primera vista no sería de mayor ayuda.
Ahora bien, si una variable de decisión x debe cumplir la restricción x≥a, para una constante a positiva, se puede imponer un cambio de variables y=x-a, que define una nueva variable y que tiene solo una restricción de no negatividad y simplifica imponer la primera como una restricción general en la aplicación del Método Simplex.
El concepto anterior nos permite hacer lo siguiente: Y1=X1-20>=0; Y2=X2-20>=0. Es decir X1=Y1+20 y X2=Y2+20. En consecuencia podemos reescribir el modelo original de la siguiente forma:
Reduciendo términos semejantes se obtiene:
Notar que este nuevo modelo de optimización se puede resolver de forma directa a través del Método Simplex, incorporando las variables no negativas Y3, Y4 e Y5 como holguras de las restricciones 1, 2 y 3, respectivamente. De esta forma el problema en su forma estándar proporciona la siguiente tabla inicial: (Notar que el valor de la función objetivo inicialmente es 1.100 debido a que dicha constante se obtiene luego de realizar el cambio de variables)
La variable Y1 entra a la base al ser la variable no básica con el costo reducido más negativo. Luego para determinar la variable básica que deja la base calculamos el mínimo cuociente: Min {420/6; 140/1; 160/2} = 70 ==>Y3 sale de la base. Se realiza una iteración del Método Simplex:
Ahora Y2 entra a la base al ser la única variable no básica con costo reducido negativo. A continuación la variable que deja la base se determina a través del criterio del mínimo cuociente: Min {70/1/2; 70/3/2; 20/1} = 20 ==>Y5 sale de la base. Se realiza una nueva iteración:
Se ha alcanzado la tabla óptima donde Y1=60 e Y2=20 con valor óptimo V(P)=3.400. Reemplazando en las variables originales se obtiene la solución óptima del problema original: X1=60+20=80 y X2=20+20=40. Se puede corroborar que esta solución óptima al ser evaluada en la función objetivo del problema inicial proporciona el valor óptimo del modelo de programación lineal: Max 30*(80)+25*(40)=3.400, lo que permite garantizar la equivalencia del procedimiento utilizado.