La Programación Lineal como hemos analizado anteriormente provee una forma eficiente para enfrentar el problema de cómo reducir la duración de un proyecto de la forma más económica posible (Análisis de Crashing) en el contexto de la aplicación del Método de Ruta Crítica (CPM) para la gestión de proyectos. Adicionalmente en algunas situaciones se suele enfrentar costos de penalización en la medida que el proyecto se entregue más tarde de lo comprometido o estimado, como también incentivos por entregas anticipadas que no vayan en desmedro de la calidad del proyecto.
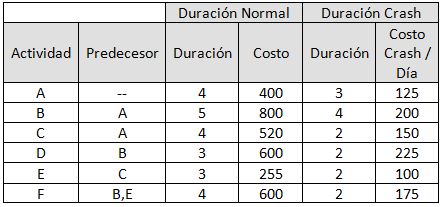
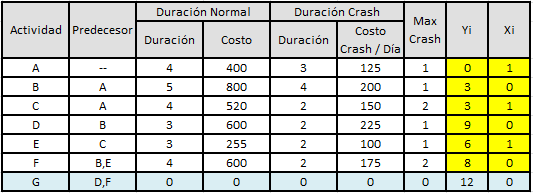
Consideremos el siguiente ejemplo para el cálculo de la Duración Óptima de un Proyecto (el tiempo está medido en días y el costo en dólares):
Por ejemplo la Actividad F tiene una duración normal de 4 días a un costo de 600 dólares y se puede comenzar una vez terminadas las Actividades B y E (predecesores). Si se desea apurar (hacer «crash») en la Actividad F, el menor tiempo que se puede adoptar es de 2 días (es decir, la reducción máxima es 2 días), donde por cada día que se reduce la duración de dicha actividad se incurre en un costo adicional de 175 dólares. De esta forma, por ejemplo, si se quisiera reducir la duración de la Actividad F de 4 a 3 días, el costo sería de 775 dólares (600+175).
Asuma que la fecha de entrega del proyecto es el día 10. La compañía debe pagar 170 dólares por cada día de atraso. Encuentre el número óptimo de días que debe durar el proyecto a través del análisis de crashing y el costo total del proyecto (incluyendo posibles multas por atraso).
Indique claramente las actividades donde realice crashing. Dibuje el diagrama del proyecto de la alternativa que se propone (el proyecto con el costo más bajo), representando el nombre de cada actividad al interior de los respectivos nodos. Para cada actividad calcule los siguientes indicadores: IC, TC, IL, TL. Luego obtenga explícitamente la holgura de cada actividad y la(s) ruta(s) crítica(s) del proyecto.
A continuación se define un modelo de optimización lineal propuesto para abordar el problema:
Variables de Decisión:
Parámetros:
Función Objetivo: Consiste en minimizar el costo de terminar el proyecto en K días, donde 3.175 corresponde al costo en dólares de desarrollar el proyecto con las actividades en tiempo normal y la expresión en la sumatoria es el costo incremental de disminuir la duración del proyecto.
Restricciones:
Cada actividad se puede reducir (de ser posible) dentro del límite máximo de reducción permisible:
Relaciones de predecesores entre las actividades y el tiempo de inicio y reducción:
Definición del tiempo objetivo para el proyecto:
No negatividad de las variables de decisión:
Una vez definido el modelo de Programación Lineal se implementa computacionalmente haciendo uso de Solver de Excel. Para ello será necesario sensibilizar los resultados del modelo para valores del parámetro K en el intervalo de [10,15] días (el lector puede corroborar que la duración del proyecto si cada actividad mantiene su duración normal es de 15 días). La solución óptima se resume a continuación:
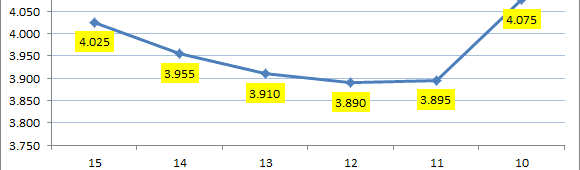
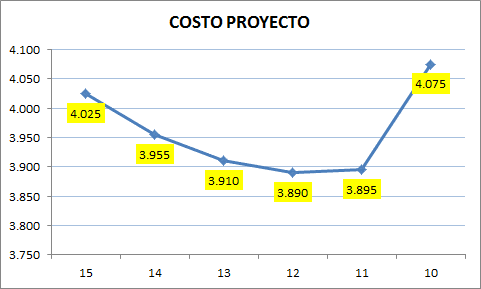
El tiempo óptimo para completar el proyecto corresponde a 12 días, con un costo total (incurriendo multas por atraso) de 3.890 dólares. El gráfico a continuación muestra el valor de la función objetivo (costo total) para distintos valores de duración del proyecto.
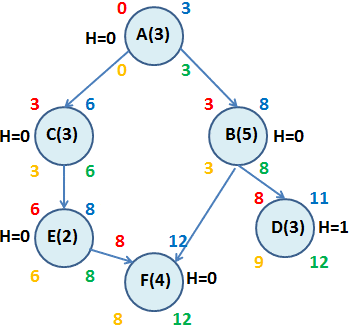
A continuación desarrollamos el diagrama del proyecto donde se observa que existen 2 rutas críticas: A-B-F y A-C-E-F, con una duración de 12 días. Notar que la única actividad que no es crítica con holgura positiva (de 1 día) es la Actividad D.
¿Quieres tener el archivo Excel con la resolución en Solver de este problema?
[sociallocker]Crashing Óptimo[/sociallocker]


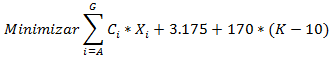
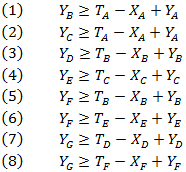
Hola, sólo quiero hacer la observación de que en la función objetivo, el sumando 3.175, por ser una constante, no debe incluirse en la misma. Gracias y saludos.
@Francisco. Gracias por tu comentario. No hay problema en incluir la constante en la función de objetivo dado que Min f(x) + constante = constante + Min f(x). Por supuesto se puede omitir la constante de la función objetivo y luego simplemente sumar dicho valor al valor óptimo que se obtenga. Saludos.
Hola la respuesta que busco con este tema se refiere a la definición de la solución óptima, que se relacione con mi proyecto de tesis, y la verdad que no encontrado solución clara a que se refiere en realidad. Mi proyecto trata de un Centro Educativo Infantil. Se agradece su ayuda, gracias y saludos.
@jenny. Puedes escribirnos a info@gestiondeoperaciones.net detallando el caso particular de tu proyecto de tesis de modo de poder evaluar si te podemos dar una sugerencia más específica a tus requerimientos.
Me parece bastante interesante el artículo, sobre todo muy didáctico, de fácil entendimiento. Felicidades