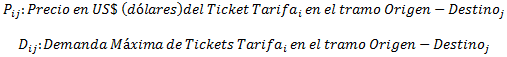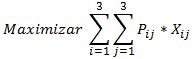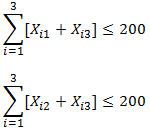La industria de transporte de pasajeros enfrenta diariamente el problema de determinar cómo asignar de forma eficiente su capacidad de transporte al momento de ofrecer distintos tipos de tarifas a sus clientes para una ruta específica. Para ello se debe considerar de forma simultanea los ingresos por venta asociados a cada tipo de tarifa, una estimación de demanda de los clientes por dichas tarifas y la capacidad del medio de transporte en términos de la cantidad de asientos.
El siguiente problema considera la formulación y resolución computacional de un Problema de Asignación de capacidad de un avión para una empresa de transporte aéreo. La complejidad del problema y el nivel de detalle de la información se ha simplificado para fines académicos.
Problema de Asignación de Capacidad de un Avión
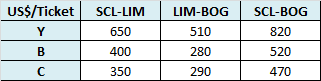
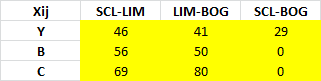
Consideremos una línea aérea que realiza la ruta Santiago (Chile) a Bogotá (Colombia) con escala en Lima (Perú). Para dicha ruta utiliza un avión con capacidad de 200 pasajeros. El departamento de ventas ha estimado los precios de mercado (en dólares) para las combinaciones de origen destino de 3 tipos de tarifas que actualmente ofrece la empresa: «Tarifa Y» (primera clase), «Tarifa B» (estándar) y «Tarifa C» (turista).
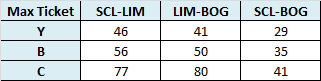
Adicionalmente y según información histórica de esta ruta, la línea aérea ha estimado el número máximo de pasajes que los clientes demandarán por cada combinación de tarifa en un tramo del vuelo. Por ejemplo la demanda máxima esperada para el tramo Santiago (SCL) a Bogota (BOG) en la Tarifa B es de 35 tickets.
Con esta información la línea aérea desea determinar cómo asignar la capacidad del avión de modo de ofrecer un determinado número de pasajes para cada tipo de tarifa en un tramo del vuelo. Para ello definiremos el siguiente modelo de Programación Lineal:
Variables de Decisión:
Donde i=1,2,3 representa los distintos tipos de tarifa (Y, B y C, respectivamente) y j=1,2,3 las combinaciones de origen destino (SCL-LIM, LIM-BOG y SCL-BOG, respectivamente).
Parámetros:
Al utilizar una notación con parámetros podemos representar el modelo de optimización de forma compacta.
Función Objetivo:
Restricciones:
Se ofrece para cada tarifa en las combinaciones origen destino un número de tickets que no supere la demanda máxima del mercado.
Para cada tramo del vuelo se debe respetar la capacidad total del avión de 200 pasajeros.
Cuando el avión despega desde Santiago con destino Lima lleva pasajeros con destino tanto a Lima como Bogotá. Por tanto independiente de la tarifa que cada uno de estos pasajeros haya pagado (por ello la sumatoria en las tarifas) no pueden superar la capacidad total del avión. Lo anterior esta garantizado por la primera restricción de capacidad.
La segunda restricción de capacidad es para el tramo desde Lima a Bogotá, donde se consideran adicionalmente los pasajeros que vienen desde Santiago.
Finalmente se definen las condiciones de no negatividad.
Al resolver con Solver el problema anterior se alcanza la siguiente solución óptima que determina cuántos pasajes debería ofertar la línea aérea para cada combinación de tarifa y origen destino.
El valor óptimo del problema que representa los ingresos totales (en dólares) asociados a la solución óptima propuesta es de US$158.340.
¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.
[sociallocker]Descarga Aquí el Archivo[/sociallocker]