Una de las aplicaciones clásicas de la Investigación de Operaciones y en particular de la Programación Lineal es proponer alternativas óptimas para el proceso logístico o transporte de insumos o productos desde un conjunto de oferentes hasta un conjunto de destinatarios o demandantes.
Cuando consideramos que en este proceso de transporte pueden participar intermediarios estamos frente a una extensión del modelo básico de transporte el cual es comúnmente conocido como Modelo de Transporte con Transbordo. A continuación presentaremos un caso aplicado de dicho modelo.
Ejemplo Problema de Transporte con Transbordo
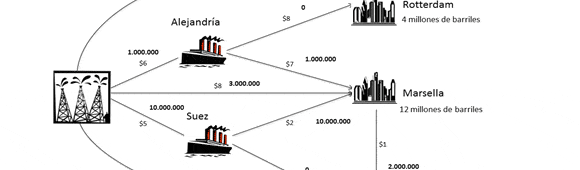
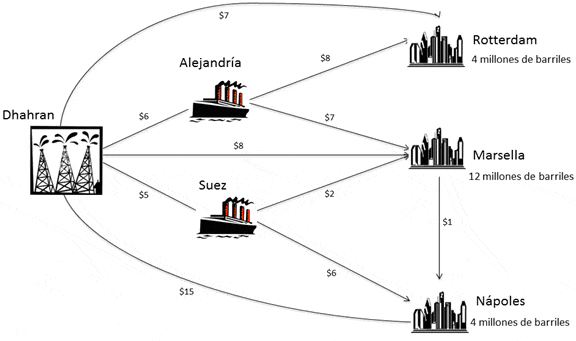
Se deben transportar 20 millones de barriles de petróleo desde Dhahran en Arabia Saudita a las ciudades de Rotterdam, Marsella y Nápoles en Europa. Las demandas de estas tres ciudades son 4, 12 y 4 millones de barriles, respectivamente. A continuación se presenta un diagrama con las posibles rutas:
Observe que para cada ciudad existe la posibilidad directa de envío, es decir, que los barriles sean transportados directamente desde Dhahran. Sin embargo, la ruta que une Dhahran y Marsella no puede transportar más de 3 millones de barriles debido a ciertos acuerdos comerciales.
Por otro lado, existe la posibilidad que se realice una detención, ya sea en el puerto de Alejandría o Suez, donde la capacidad de almacenamiento es de 8 y 10 millones respectivamente.
Por último, observe que es posible enviar barriles de petróleo desde Marsella a Nápoles. Sin embargo, le está prohibido a Nápoles recibir más petróleo de Marsella que directamente de Dhahran. Formule y resuelva un modelo de Programación Lineal que permita hallar la política óptima de transporte para cumplir con los requerimientos de demanda de los puertos.
Variables de Decisión:
- X1: Barriles transportados desde Dhahran a Rotterdam
- X2: Barriles transportados desde Dhahran a Marsella
- X3: Barriles transportados desde Dhahran a Nápoles
- X4: Barriles transportados desde Dhahran a Alejandría
- X5: Barriles transportados desde Dhahran a Suez
- X6: Barriles transportados desde Alejandría a Rotterdam
- X7: Barriles transportados desde Alejandría a Marsella
- X8: Barriles transportados desde Suez a Marsella
- X9: Barriles transportados desde Suez a Nápoles
- X10: Barriles transportados desde Marsella a Nápoles
Función Objetivo:
Minimizar los costos totales de transportes dados por la siguiente expresión: 7X1 + 8X2 + 15X3 + 6X4 + 5X5 + 8X6 + 7X7 + 2X8 + 6X9 + 1X10
Restricciones:
Satisfacer la Demanda en los Puertos:
- X1 + X6 = 4.000.000 (Rotterdam)
- X2 + X7 + X8 – X10 = 12.000.000 (Marsella)
- X3 + X9 + X10 = 4.000.000 (Nápoles)
Notar que Marsella eventualmente podría recibir más de 12 millones de barriles de petróleo (su demanda) debido a que este Puerto tiene la posibilidad de abastecer a Nápoles.
Balance en el Transbordo:
- X4 = X6 + X7 (Alejandría)
- X5 = X8 + X9 (Suez)
La cantidad de barriles que recibe Alejandría y Suez debe ser igual a lo que cada uno de ellos despacha a los Puertos, es decir, los intermediarios no acumulan inventario al final del periodo de planificación. En este punto es importante destacar que si se considera un modelo extendido donde se busca satisfacer los requerimientos de demanda de varios periodos podría ser admisible almacenar inventario en Alejandría y Suez, cambiando en este caso la forma del modelo de optimización.
Capacidad de Procesamiento en el Transbordo:
- X4 <= 8.000.000 (Alejandría)
- X5 <= 10.000.000 (Suez)
Tanto Alejandría como Suez no pueden recibir una cantidad de barriles mayor a la que pueden procesar.
Capacidad Ruta entre Dhahran y Marsella:
- X2 <= 3.000.000
La ruta que une Dhahran y Marsella no puede transportar más de 3 millones de barriles por acuerdos comerciales.
Cantidad Recibida por Nápoles:
- X3 >= X10
Está prohibido a Nápoles recibir más petróleo de Marsella que directamente de Dhahran.
No Negatividad:
- Xi >= 0 Para todo i
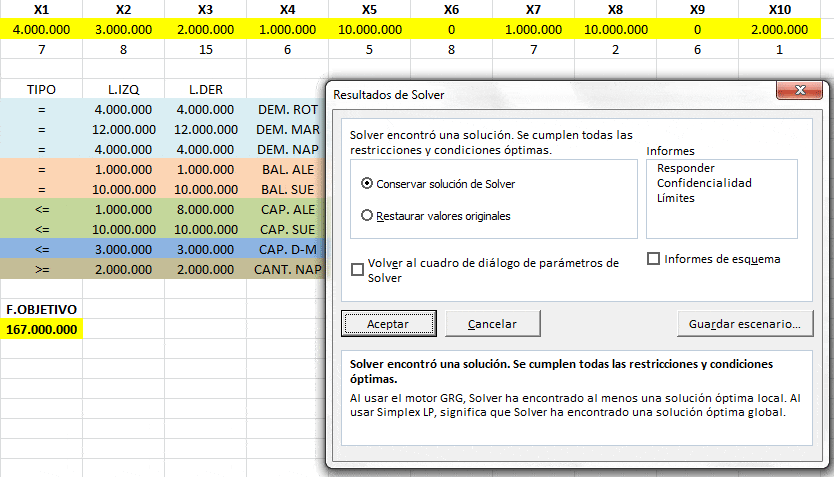
Al implementar el modelo anterior con Solver de Excel se obtienen los siguientes resultados:
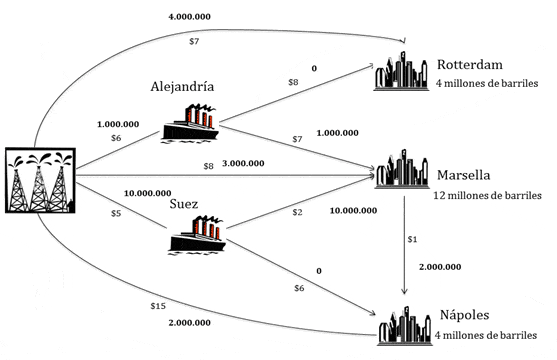
Donde la solución alcanzada tiene la siguiente estructura (sobre los arcos se detalla el valor de la solución óptima):
Excelente Material de Estudio….Felicitaciones, y muchas gracias por el aporte.
Saludos desde CHILE