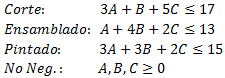Una empresa de Rústicos “El Viejo Baúl” fabrica entre muchos otros productos tres tipos de sillas A, B y C, las cuales se venden a precio de 11, 13 y 12 dólares cada una y respectivamente. Las sillas pasan por tres procesos, Corte, Ensamblado y Pintado, para lo cual se dispone máximo de 17, 13 y 15 horas respectivamente a la semana para dedicar a estas operaciones a estos productos. La silla tipo A requiere 3 horas para corte, 1 hora para ensamblado y 3 horas para pintura. La silla tipo B requiere 1 hora para corte, 4 horas para ensamblado y 3 horas para pintura. Y finalmente la silla tipo C, requiere de 5 horas para corte, 2 para ensamblado y 2 horas para pintura. De acuerdo a la anterior información:
a. Resuelva el problema con variables continuas y señale los resultados para cada variable.
Variables de Decisión: Se estable el nivel de producción semanal para cada una de las variedades de silla según se detalla a continuación:
Función Objetivo: Maximizar los ingresos semanales asociados a la producción y venta de las sillas.
Restricciones: En los procesos de corte, ensamblado y pintura se debe respetar la disponibilidad de horas semanales. Adicionalmente se deben satisfacer las condiciones de no negatividad.
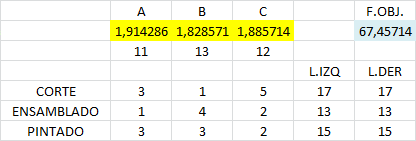
La implementación computacional del problema anterior con Solver de Excel permite alcanzar los siguientes resultados:
Donde la solución óptima es A=1,914286, B=1,828571 y C=1,885714 con valor óptimo V(P)=67,45714.
b. Modifique las condiciones de las variables y elíjalas enteras (integer) y observe el cambio entre la respuesta del punto a y esta nueva hallada.
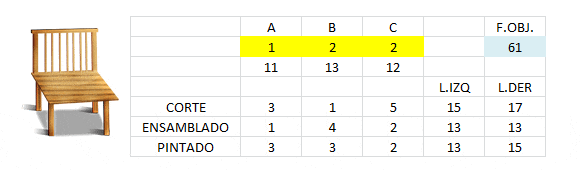
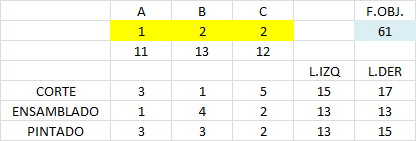
Al definir las variables de decisión enteras estamos frente a un modelo de Programación Entera (siendo el escenario inicial un problema de Programación Lineal). Los resultados son:
La solución óptima es A=1, B=2 y C=2 con valor óptimo V(PE)=61.
c. Concluya qué sucedió entre variables continuas y variables enteras.
Es importante observar que el dominio de soluciones factibles del problema entero (parte b) es un subconjunto del dominio de soluciones factibles del problema lineal (parte a). Por tanto es natural que al no obtener una solución con valores enteros para las variables de decisión en el problema inicial, el valor óptimo necesariamente disminuirá en la variante entera de dicho problema de maximización (V(PE)<V(P)). También se puede destacar que la solución entera no necesariamente se alcanza al aproximar los resultados fraccionarios de una solución de un problema lineal al entero inferior o superior más cercano. En consecuencia, para abordar de forma eficiente la resolución de un modelo que considere valores enteros para las variables de decisión requiere de una alternativa algorítmica específica como por ejemplo el Método Branch and Bound.
A continuación encontrarás un enlace de descarga del archivo Excel utilizado para la resolución del problema de corte, ensamblado y producción de sillas. En el archivo se incluyen 2 hojas que corresponden a la parte a) y b) del problema propuesto. Produccion de Sillas.