La Programación Entera provee una forma eficiente de enfrentar los problemas de selección de proyectos a ejecutar dentro de una cartera de potenciales proyectos a realizar, donde cada uno de éstos tiene asociado un tiempo de ejecución, requerimientos de fondos de inversión y necesidades adicionales. El siguiente artículo aborda la formulación de un modelo de optimización de Programación Entera que permita seleccionar los proyectos a realizar que maximice el Valor Presente Neto (VPN) del conjunto, respetando restricciones presupuestarias, políticas de inversión y de disponibilidad de personal.
Problema de Selección de Cartera de Proyectos
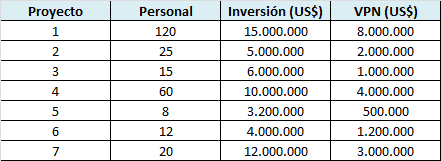
Consideremos una empresa que tiene en carpeta 8 proyectos, cada uno de los cuales con una estimación del VPN, la necesidad de financiamiento (en dólares) y los requerimientos de personal. La información se resume en la siguiente tabla:
Por ejemplo, el Proyecto 1 requiere de 120 profesionales para ser realizado, con una inversión inicial de 15 millones de dólares y representa un Valor Presente Neto (VPN) de 8 millones de dólares. Asumiremos que la empresa dispone de 155 profesionales, un presupuesto para inversión de 40 millones de dólares. Adicionalmente para efectos de minimizar el riesgo la empresa debe ejecutar al menos 4 proyectos. Los proyectos 3 y 6 son excluyentes, es decir, sólo uno de los 2 puede ejecutarse.
Variables de Decisión:
Probablemente el lector se pregunte si es equivalente definir Xi: dólares a invertir en el Proyecto i. El problema subyacente a dicha formulación es asumir que si, por ejemplo, se invierte 7,5 millones de dólares en el Proyecto 1 se obtiene un VPN de 4 millones de dólares, es decir, que el VPN es proporcional al dinero invertido. Recordar que la proporcionalidad es un supuesto básico de la Programación Lineal donde claramente no provee una forma realista de representación en este caso, donde la naturaleza de la decisión es realizar o no un proyecto, sin dejar espacio para decisiones «intermedias».
Función Objetivo:
Consiste en maximizar la sumatoria del Valor Presente Neto de los proyectos (en millones de dólares). En este contexto el valor óptimo corresponderá a la suma del VPN de aquellos proyectos que finalmente se llevaran a cabo.
Restricciones:
Se debe respetar la disponibilidad de trabajadores:
La inversión total no puede superar el presupuesto disponible:
Al menos se deben realizar 4 proyectos para efectos de diversificación del riesgo:
Los proyectos 3 y 6 son excluyentes:
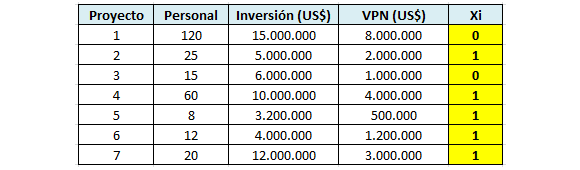
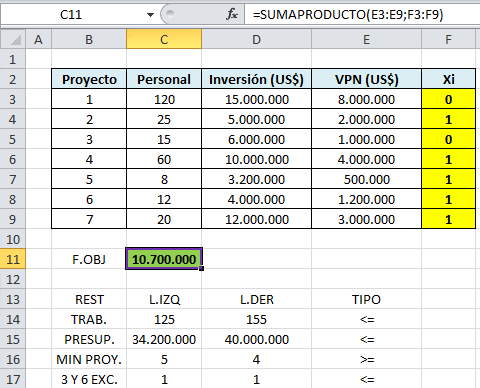
Luego de implementar computacionalmente el problema anterior con Solver se alcanza los siguientes resultados:
La solución óptima consiste en desarrollar los proyectos 2, 4, 5, 6 y 7 lo que reporta un VPN de 10,7 millones de dólares (valor óptimo).
¿Quieres tener el archivo Excel con la resolución en Solver de este problema?. Recomiéndanos en Facebook, Google+ o Twitter utilizando la herramienta de redes sociales a continuación y accede de forma gratuita e inmediata a la descarga del archivo (el enlace de descarga con el nombre «Descarga el Archivo» se mostrará abajo una vez que nos hayas recomendado).
[l2g name=»Descarga el Archivo» id=»4355″]
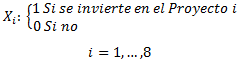
Muy buenos ejercicios de aplicación