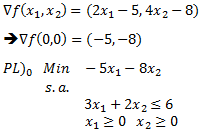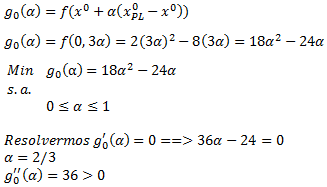alfa Archivos - Gestión de Operaciones

Suavizamiento Exponencial Simple (Ejercicios Resueltos)

El método de Suavizamiento Exponencial Simple (conocido también como Alisamiento Exponencial o Suavización Exponencial Simple) corresponde a una de las metodologías más populares para realizar Pronósticos de Demanda al disponer de una serie de tiempo. En este contexto en el artículo Pronóstico de Demanda con Alisamiento Exponencial para distintos valores de Alfa se detalla la aplicación de este método simulando su comportamiento y ajuste a los datos de la demanda real para distintos valores del parámetro de suavización alfa (α). A continuación presentaremos un compendio de ejercicios resueltos de Suavizamiento Exponencial Simple y un resumen de los principales conceptos tras este método.

El pronóstico del período t ( $F_{t}$ ) será igual al pronóstico del período anterior, es decir, del período t-1 ( $F_{t-1}$ ) más alfa (α) por el error del período anterior ( $A_{t-1}-F_{t-1}$ ), según se muestra en la fórmula a continuación:

Ejercicios Resueltos de Suavizamiento Exponencial Simple

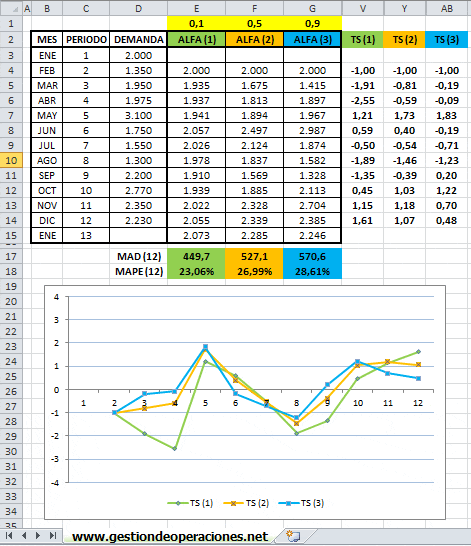
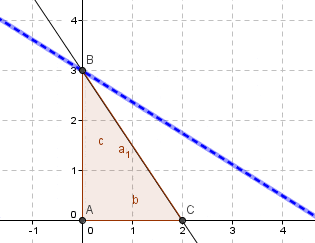
Ejercicio N°1: Una empresa de consumo masivo lleva registro de la demanda mensual de uno de sus productos emblemáticos para un período de un año. Dicha información se presenta en la columna etiquetada Demanda en la imagen a continuación. Se requiere utilizar el método de suavizamiento exponencial simple considerando tres valores para el parámetro de suavizamiento alfa: 0,1; 0,5 y 0,9. Obtener el pronóstico del período 13 (mes de Enero del año siguiente) y evaluar el ajuste del método para cada uno de los valores de alfa propuestos.

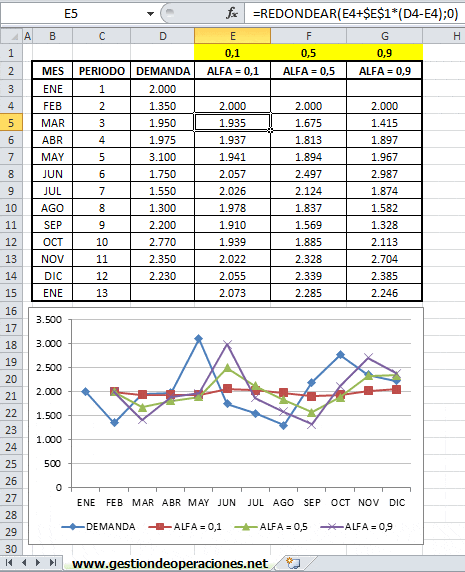
Recordar que el suavizado exponencial simple requiere de un primer pronóstico para su aplicación. En este caso hemos decidido generar un pronóstico a contar del segundo período (mes de Febrero) y asumir que dicho valor corresponde a la demanda real del mes anterior (mes de Enero o período 1). Este criterio por cierto es arbitrario y se podría seleccionar otro punto de partida, por ejemplo, un promedio para la demanda real de los 12 meses.

Adicionalmente en las columnas E, F y G de la imagen anterior se observa los pronósticos para alfa 0,1, 0,5 y 0,9, respectivamente. En particular se puede corroborar la fórmula utilizada para obtener el pronóstico del mes de Febrero utilizando α=0,1 (celda E5), donde los resultados han sido aproximados al entero más cercano.

Ejercicio N°2: Considerando la información del Ejercicio N°1 ¿Cuál de los 3 métodos tiene asociado una menor Desviación Absoluta Media (MAD)?.

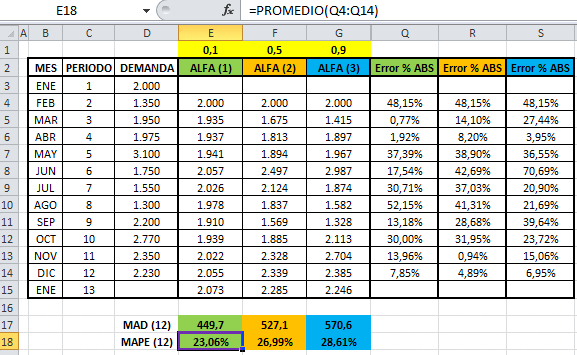
Para obtener el MAD (Mean Absolute Deviation) o Desviación Absoluta Media, aplicamos el procedimiento descrito en el artículo Calculo del MAD y la Señal de Rastreo para un Pronóstico de Demanda. En la planilla interactiva a continuación puedes simular tanto los pronósticos como el comportamiento del MAD para distintos valores de alfa. Para ello basta con editar las celdas en color amarillo.

En caso de obtener un error del tipo #VALUE! ingrese los valores de α utilizando . (punto) como separador de decimal, por ejemplo, α=0.1.

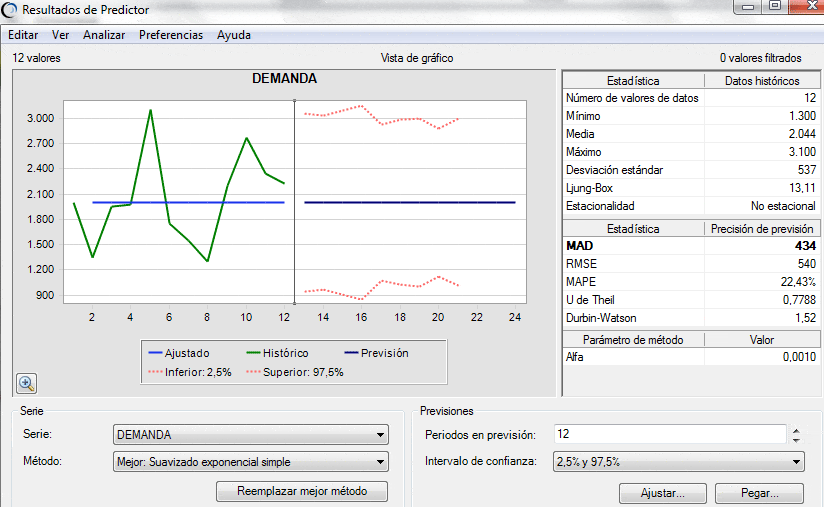
Conclusión: El alfa que provee el menor MAD al período 12 entre las 3 alternativas evaluadas (0,1, 0,5 y 0,9) es α=0,1 (MAD de 449,7). En efecto se puede corroborar utilizando el módulo Predictor de Crystal Ball (según se describe en Cómo utilizar el Módulo Predictor en Crystal Ball para Promedio Móvil Simple y Suavizado Exponencial Simple) que α=0,001 es el valor de alfa que minimiza el MAD en este ejemplo.

Ejercicio N°3: Asuma nuevamente la información del Ejercicio N°1 ¿Cuál de los 3 métodos tiene asociado un menor Error Porcentual Absoluto Medio (MAPE)?.

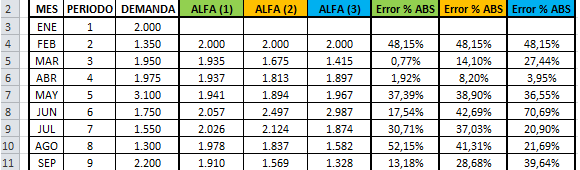
A continuación se presentan los resultados del cálculo del MAPE donde en particular se puede observar que la fórmula de cálculo es simplemente el promedio de los errores absolutos en términos porcentuales. Luego se concluye que al igual que en el Ejercicio N°2 el parámetro alfa que tiene mejor desempeño en relación al MAPE es α=0,1.

Observación: En la pantalla de los resultados obtenidos con Predictor de Crystal Ball se observa que para α=0,001 el valor del MAPE es 22,43%. Te recomendamos verificar el resultado anterior haciendo uso del procedimiento anteriormente descrito.

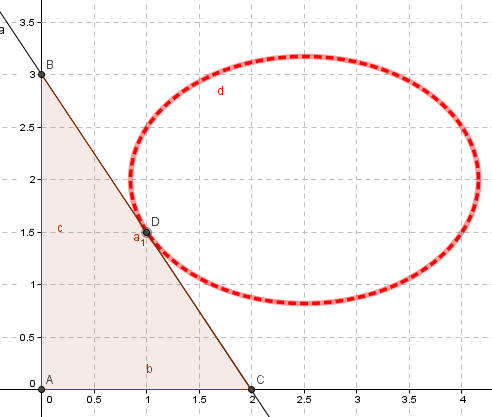
Ejercicio N°4: Calcule y grafique la Señal de Rastreo (Tracking Signal o TS) para los métodos aplicados en el Ejercicio N°1.

Se observa que la Señal de Rastreo se encuentra en los límites comúnmente aceptados [-4,4] MAD. Adicionalmente no se observa una tendencia evidente en su comportamiento por lo cual no se evidencia la presencia de error sistemático. Criterios y antecedentes similares sobre la interpretación conceptual de este indicador de desempeño se aborda en el artículo Interpretación de la Señal de Rastreo de un Pronóstico de Demanda.

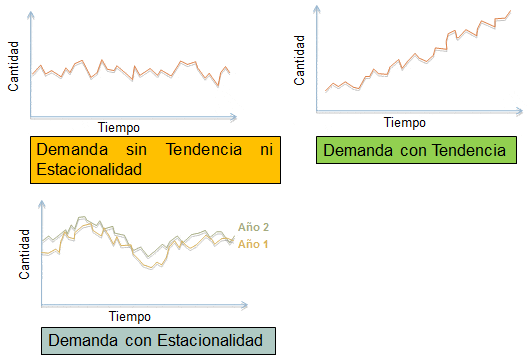
Conclusión: En general el método de Suavizamiento de Exponencial Simple tiene un mejor desempeño cuando la serie de tiempo no presenta tendencia ni estacionalidad marcada. En el caso de evidenciar alguno de estos componentes en la serie de tiempo (o ambos de forma simultanea) se recomienda explorar otros métodos de pronóstico como el Método de Suavizamiento Exponencial Ajustado a la Tendencia (Suavización Exponencial Doble) o el Método de Descomposición (entre otros).

Ejemplo del Método de Frank Wolfe en Programación No Lineal

El método o algoritmo de Frank Wolfe fue propuesto en 1956 por Marguerite Frank y Philip Wolfe y se aplica a problemas de optimización matemática con una función objetivo no lineal convexa y cuyo dominio de soluciones factibles esta compuesto exclusivamente por restricciones lineales, es decir, es un conjunto convexo (en consecuencia el problema es convexo).

Consideremos el siguiente problema que asumiremos cumple con el formato anteriormente descrito:

Dada una aproximación $x^{k}$ a la solución óptima del problema, podemos resolver un problema más sencillo que aproxime al problema P), suponiendo $x^{k}$ factible.

O equivalentemente resolviendo el siguiente problema:

Que puede ser resuelto mediante el Método Simplex. Denotamos por $x_{PL}^{k}$ la solución óptima de $PL_{k}$ . El método contempla en seguida una minimización de un problema unidimensional que equivale a escoger un escalar $\alpha _{k}$ de modo que:

En seguida se define la siguiente aproximación al óptimo como:

Que equivale a definir $x^{k+1}$ como la solución óptima de f restringida al conjunto de puntos que determina al segmento que une $x^{k}$ con $x_{PL}^{k}$ .

Ejemplo: Aplicar el método de Frank Wolfe al siguiente problema no lineal restringido (convexo). Notar que la matriz hessiana o de segundas derivadas de la función objetivo es positiva definida.

Realizamos la primera iteración del método que da origen al siguiente problema de Programación Lineal:

La resolución es trivial y puede ser alcanzada de forma gráfica con Geogebra. La solución óptima es $x_{PL}^{0}=(0,3)$ según se aprecia a continuación:

Luego buscamos la solución para el problema unidimensional en términos del parámetro $\alpha$ :

Finalmente se obtiene $x^{1}=x^{0}+\frac{2}{3}(x_{PL}^{0}-x^{0})=(0,2)$ concluyendo una iteración del método de Frank Wolfe. Se propone al lector seguir las iteraciones a contar de este punto. Por ejemplo se puede verificar que $x_{PL}^{1}=(2,0)$ . (Hint: La solución óptima se alcanza en $(x_{1},x_{2})=(1,\frac{3}{2})$ .

Cómo construir una Curva Característica de Operación (CO) con Excel

La Curva Característica de Operación (o Curva Característica Operativa) consiste en una representación gráfica que muestra para un plan de muestreo específico (n,c) la probabilidad de aceptación del lote, para varios valores de calidad del lote a la entrada p (% de unidades defectuosas). Una Curva Característica de Operación tendrá entre sus puntos uno definido por el NCA y 1-α y otro punto definido por PTDL y β.

Para determinar la probabilidad de aceptación de un lote, se pueden utilizar las distribuciones Binomial o Poisson. Cuando el tamaño de la muestra es al menos 15 unidades (n>15), el tamaño del lote es al menos 10 veces el tamaño de la muestra (N>10*n) y el porcentaje de unidades defectuosas históricamente es menor a un 10% (p<10%), es preferible la Distribución de Poisson debido a la facilidad de los cálculos.

Consideremos el siguiente ejemplo: Un fabricante de pistones para motocicletas comenzará a vender diariamente 1.200 unidades para un nuevo cliente. Este último determina condiciones contractuales para la inspección del lote diario, especificando que tomará muestras de 100 unidades (n=100) y que sólo aceptará los pedidos con 4 o menos defectos (c=4). El fabricante menciona en el contrato, que históricamente ha obtenido un porcentaje defectivo del 2% (p=2%). Determinar la probabilidad de aceptación del lote por parte del cliente.

Para determinar la probabilidad de aceptación del lote podemos utilizar la siguiente fórmula haciendo uso de una planilla de cálculo Excel: =POISSON(4;100*2%;VERDADERO). En consecuencia la probabilidad de aceptación del lote por parte del cliente es de un 94,73% (aproximado).

Una alternativa a Excel para estos efectos es hacer uso de la herramienta de cálculo de probabilidades del software Geogebra donde se debe ingresar los parámetros de la distribución µ (equivalente a n*p=100*2%=2) y el valor correspondiente al número de aceptación c (en la imagen c=4).

De esta forma se puede extender el procedimiento calculando la probabilidad de aceptación del lote Pa para distintos valores de calidades a la entrada p. Un extracto de ello se presenta en la siguiente tabla:

A continuación se construye un gráfico con la Curva Característica de Operación. Se ha destacado con una etiqueta color amarillo el dato que hemos calculado previamente.

En un próximo artículo discutiremos el impacto que tiene en el plan de muestreo y en particular en la Curva Característica de Operación un cambio en el tamaño de la muestra o un cambio en el número de aceptación.

Cómo determinar el Tamaño de la Muestra y el Número de Aceptación en un Muestro de Aceptación

Un muestreo de aceptación simple esta definido por el número de unidades en la muestra n y el número de aceptación c. El tamaño de la muestra n puede variar entre una unidad hasta incluso todos los artículos del lote (que en general se representa por N). En tanto el número de aceptación c determina el número máximo de artículos defectuosos que se pueden encontrar en una muestra antes de rechazar el lote.

En este contexto determinar los valores de n y c es un asunto crítico en todo muestreo de aceptación. Dichos valores se obtienen mediante la interacción de 4 factores, a saber: NCA (Nivel de Calidad Aceptable o AQL: Acceptable Quality Level), α, PTDL (Porcentaje de Tolerancia de Defectos en el Lote o LTPD: Lot Tolerance Percent Defective) y β.

Por una parte al fabricante le interesa que el plan de muestreo tenga una probabilidad baja de rechazar lotes buenos. En tanto el objetivo del consumidor es asegurarse que el plan de muestreo tenga una probabilidad baja de aceptar lotes malos. Se considera que los lotes son de alta calidad si contienen no más de un nivel específico de unidades defectuosas (NCA). Por el contrario un lote es de baja calidad si el porcentaje de defectos es mayor que una cantidad específica (PTDL).

La probabilidad asociada con el rechazo de un lote de alta calidad o α se conoce como riesgo del productor. Análogamente la probabilidad relacionada con la aceptación de un lote de baja calidad o β es el riesgo del consumidor.

Consideremos la siguiente adaptación de un ejemplo extraído del Libro Administracion De Operaciones de Chase, Jacobs y Aquilano (Duodécima Edición).

Una empresa fabrica scaners de radar que se utilizan para detectar trampas de velocidad. Las tarjetas de circuito impreso de los scaners se comprar a un distribuidor externo. El distribuidor produce las tarjetas con un NCA de un 2% y está dispuesto a correr un riesgo de un 5% (α) de que se rechacen lotes con este nivel o menor número de defectos. La empresa considera inaceptables los lotes con 8% o más defectos (PTDL) y quiere asegurarse de que aceptará esos lotes de baja calidad no más del 10% de las veces (β). Se acaba de entregar un lote grande. ¿Qué valores de n y c se deben seleccionar para determinar la calidad de este lote?.

Los parámetros del problema son NCA=2%, α=5%, PTDL=8% y β=10%. A continuación para determinar n y c consideramos un extracto de una tabla de un plan de muestreo para α=5% y β=10%.

En primer lugar se divide PTDL/NCA=8%/2%=4. A continuación en la columna 2 de la tabla anterior se busca la razón que se mayor o igual al cuociente 4. Este valor es 4,057 que está asociado a c=4. Finalmente encontrar el valor en la columna 3 que está en la misma fila que c=4 y luego dividir es cantidad entre NCA para obtener n (1,970/2%=98,5). En consecuencia el plan de muestre apropiado es (n,c)=(99,4).

Para determinar la eficiencia del plan de muestreo al discriminar entre lotes buenos y malos para valores intermedios se propone construir una Curva Característica de Operación (CO). Estas curvas son únicas para cada combinación de n y c e ilustran la probabilidad de aceptar lotes con diversos porcentajes de defectos.

Por ejemplo si el porcentaje de defectos es de un 2% (NCA) la probabilidad de aceptación es de un 95%, por tanto existe un α=5% (1-0,95) de rechazar un lote de alta calidad (riesgo del productor). En tanto para un porcentaje de defectos de un 8% (PTDL) existe una probabilidad de un 10% de aceptar un lote de baja calidad (riesgo del consumidor).