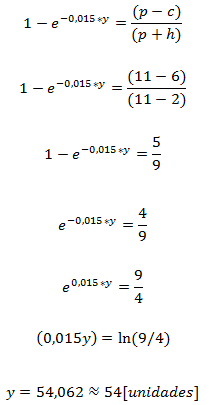distribución exponencial Archivos - Página 2 de 2

Propiedad de Falta de Memoria o Amnesia de la Distribución Exponencial

En el análisis del comportamiento de las Líneas de Espera, se reconoce que el proceso de llegada de los clientes al sistema ocurre de forma totalmente aleatoria. Se entiende por aleatorio que la ocurrencia de un evento no se ve afectado por el tiempo transcurrido desde la ocurrencia de un evento anterior. Por ejemplo, si en estos momentos son las 10:30 y la última llegada de un cliente fue a las 10:15, la probabilidad de que la siguiente llegada sea a las 10:35 es función sólo de las 10:30 a las 10:35 y en consecuencia es totalmente independiente del tiempo transcurrido desde la ocurrencia del último evento, es decir, de las 10:15 a las 10:30. Este resultado se conoce como falta de memoria o amnesia de la Distribución Exponencial.

Consideremos el siguiente ejemplo que permite ilustrar esta situación: Una máquina en operación tiene una unidad de reserva para sustituirla de inmediato cuando falla. El tiempo medio entre fallas (conocido también como MTBF o Mean Time Between Failures) se distribuye exponencial y sucede cada 50 minutos (en promedio). El operario de la máquina comenta que ésta suele descomponerse cada tarde a eso de las 17:00. Se requiere analizar la validez de lo que señala el operario.

El tasa promedio de fallas de la máquina es $\lambda =60/50=1,2[fallas/hora]$ . Luego la distribución exponencial del tiempo entre fallas se representa por $f(t)=1,2e^{-1,2t}, t>0$ .

Se concluye que lo que señala el operario no es correcto dado que contradice a que el tiempo entre fallas se distribuye exponencial y que por consiguiente es totalmente aleatorio. Dicho de otro modo la probabilidad de que la máquina falle a las 17:00 dependerá de la hora del día (en relación a las 17:00) con la que se calcule. Por ejemplo, si ahora son las 16:30, la probabilidad de que lo que afirma el operador sea cierto es:

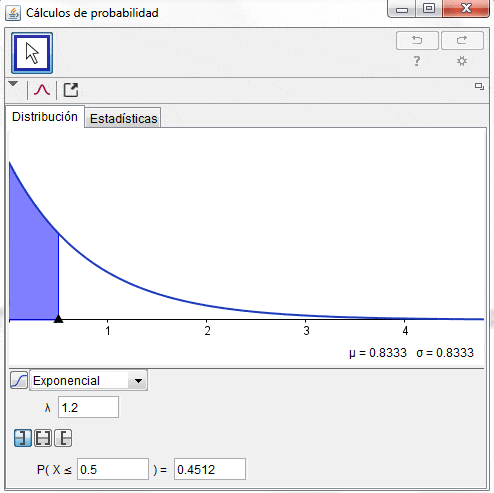
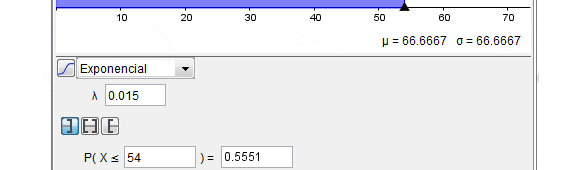
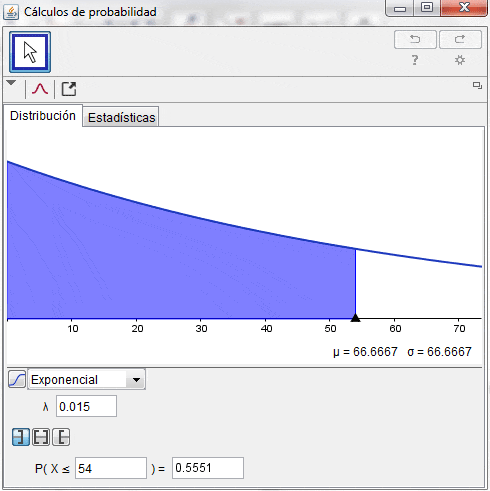
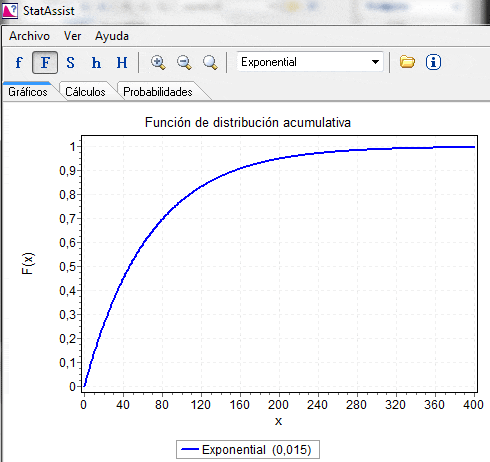
El resultado anterior se puede corroborar haciendo uso de la herramienta de cálculos de probabilidad del software Geogebra:

A continuación presentamos un breve tutorial de nuestro canal de Youtube con la implementación en Geogebra del ejemplo anterior:

Cálculo del Nivel de Servicio Instock utilizando una Demanda con Distribución Exponencial

Ejemplo Cálculo del Nivel de Servicio Instock: Un vendedor de flores tiene que decidir todas las noches cuántas flores va a llevar de su plantación a su local comercial para vender al día siguiente. La demanda por flores es estocástica y por experiencia estima que sigue una distribución exponencial con parámetro λ=0,015. El costo por flor para el vendedor es de $6 y las flores no vendidas son consignadas a $2 a un vendedor de flores secas (esto último se considera un valor de rescate o salvage value). Además se estima que el costo por cliente perdido es de $11.

En base a los antecedentes anteriores la cantidad óptima de pedido que sugiere el Modelo Newsvendor está dada por:

El nivel de servicio Instock asociado a un pedido de 54 unidades es:

Que como se aprecia corresponde a la integral definida entre 0 y 54 unidades de la función de densidad de probabilidad exponencial con parámetro λ=0,015. El resultado anterior se puede corroborar haciendo uso del software Geogebra:

De forma análoga, simplemente basta evaluar el tamaño del pedido de 54 unidades en la función de distribución exponencial para evitar el cálculo de la integral definida presentada anteriormente. En efecto:

El siguiente diagrama obtenido con el complemento StatAssist (parte de Easyfit) da cuenta de lo anterior, donde se modela una distribución exponencial (acumulada o F) con parámetro λ=0,015 y donde para un valor de x de 54 unidades F(x) es aproximadamente un 55,51%. (se puede corroborar con la fórmula de Excel =ExpCdf(54;0,015)).

Cálculo del Valor Esperado de la Información Perfecta (VEIP) en el Modelo Newsvendor

En el contexto del Modelo Newsvendor (modelo de un periodo con demanda estocástica, pero con distribución de probabilidad conocida) el Valor Esperado de la Información Perfecta (VEIP o EVPI: Expected Value of Perfect Information) es un indicador cuantitativo que mide cuán lejos la solución en promedio está de la solución perfecta, es decir, de aquella solución donde se conoce la demanda de antemano. De forma análoga el VEIP corresponde al precio que se estaría dispuesto a pagar de modo de acceder a información perfecta respecto a la realización de la demanda.

Si el valor que adoptará la demanda es conocido con antelación entonces naturalmente el tamaño óptimo de pedido será la magnitud de la demanda y=D (conocida como solución «espere y vea») lo cual permite evitar incurrir en costos asociados a un inventario insuficiente o excesivo. En dicho caso el costo esperado correspondiente será simplemente c*D donde el parámetro c representa el costo unitario de adquisición o fabricación (según sea el caso).

Luego si obtenemos el promedio de todas las realizaciones de la demanda D obtenemos el costo c*µ, donde µ es el promedio de la demanda. En consecuencia, el VEIP corresponderá a la diferencia positiva entre el costo de la solución óptima sin conocer la demanda y el costo de la solución espere y vea.

Valor Esperado de la Información Perfecta

Consideremos el siguiente ejemplo que permite ilustrar el cálculo e interpretación del Valor Esperado de la Información Perfecta (VEIP):

María es un vendedora de flores que tiene que decidir todas las noches cuántas flores va a llevar de su plantación a su local comercial para vender al día siguiente. La demanda por flores es estocástica y por experiencia estima que sigue una distribución exponencial con λ=0,04. El costo por flor para María es de $6 y las flores no vendidas son consignadas (liquidadas) a $2 cada una a un vendedor de flores secas. Además, María estima que el costo por cliente perdido es de $10.

¿Cuál es la cantidad óptima de flores que María debe llevar todos los días desde su plantación a su local comercial si desea minimizar el costo esperado? ¿Cuál es el nivel de servicio instock asociado a esta alternativa?.

La cantidad óptima de pedido en el modelo newsvendor está dada por:

Donde p representa el costo de quiebre de stock (en nuestro ejemplo por cliente perdido), c corresponde al costo de compra o producción y h el valor de consignación (en el ejemplo lo que se podría rescatar por cada unidad que no se logra vender). Considerando dicha información la cantidad óptima de flores que María debe llevar todos los días desde su plantación a su local comercial es:

Es decir, debe llevar diariamente 17 flores. Luego el nivel de servicio instock asociado a un pedido de 17 unidades es:

¿Cuál es el costo total esperado para la cantidad optima de pedido propuesta? ¿Cuál es el Valor Esperado de la Información Perfecta (VEIP)?.

El costo esperado de implementar un pedido de 17 flores es aproximadamente $219,32. A continuación calculamos el VEIP (recordar que en el caso de una distribución exponencial la media se obtiene de µ=1/λ).

Como se señalo anteriormente el VEIP establece el precio máximo que María debería estar dispuesta a pagar de modo de acceder a información perfecta respecto a la realización de la demanda de flores.

Cómo ajustar una Función de Probabilidad Teórica a una serie de datos Empíricos

En el análisis del comportamiento de una línea de espera se suele considerar la premisa de que el tiempo entre llegada de los clientes se distribuye exponencial con parámetro lambda (λ). Si bien esta presunción es válida en muchas situaciones es conveniente realizar un diagnóstico de dicha situación a través de test estadísticos ad hoc. En este contexto el siguiente artículo aborda el problema de ajuste de una función de probabilidad teórica a una serie de datos empíricos que como se menciono anteriormente es un asunto de interés en el análisis de los sistemas de espera como así también en un sin número de aplicaciones estadísticas clásicas.

La data que utilizaremos en este tutorial fue obtenida del Libro Matching Supply with Demand: An Introduction to Operations Management. Esta corresponde a las 686 llamadas que ha recibido un Call Center en un período de 4 horas según se muestra a continuación:

La pregunta que queremos responder es: ¿El tiempo entre llamada de los clientes se distribuye exponencial?. Análogamente ¿Qué función de probabilidad teórica ajusta de mejor forma los datos empíricos?. Para enfrentar dichas interrogantes utilizaremos el software Easyfit que hemos abordado en artículos anteriores para la confección de histogramas y análisis de estadísticas descriptivas.

Preliminarmente ordenaremos los datos recolectados en una columna y procedemos a calcular el tiempo transcurrido entre cada llamada (Iai), por ejemplo, entre la primera y segunda llamada pasan 23 segundos, entre la segunda y tercera llamada pasan 1 minuto y 24 segundos (equivalente a 84 segundos) y así sucesivamente. A continuación se muestra un extracto de dicho procedimiento:

Con los tiempos entre llamadas en segundos (o su equivalencia en minutos si así se desea) se hace uso de Easyfit. Copiamos dichos tiempos en la columna A tal se muestra en la siguiente imagen y luego la opción «Ajustar distribuciones»:

Luego seleccionamos «OK»:

El programa se ejecuta y proporciona los resultados de los ajustes de los datos empíricos a un importante número de distribuciones teóricas, proporcionando una estimación de los parámetros respectivos.

La distribución Wakeby es la que muestra el mejor ajuste, considerando los siguientes parámetros:

Adicionalmente podemos obtener los test de bondad de ajuste (en la pestaña «Bondad de ajuste»). Probablemente el más conocido de ellos es el test Chi-cuadrado (notar que las distribuciones han sido ordenadas en base a este criterio). También se puede obtener el detalle de las pruebas de hipótesis para distintos niveles de significancia estadística (valores de alfa).

Una interpretación exhaustiva de los test de bondad de ajuste requiere de una discusión más detallada que escapa a los propósitos de este artículo. No obstante queda de manifiesto que existen herramientas computacionales que permite simplificar este tipo de análisis que es recurrente en el ámbito de la estadística y por cierto en el de la gestión de operaciones.