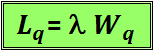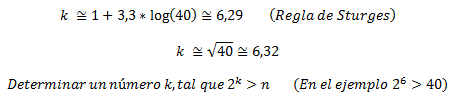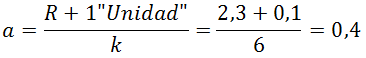La Teoría de Colas o Líneas de Espera hace uso de modelos matemáticos para encontrar un balance adecuado entre el nivel de servicio ofrecido a los clientes y los costos asociados a su prestación. El objetivo es reducir el impacto desfavorable de la espera de los clientes o usuarios de un sistema a niveles tolerables.
Notar que la tolerancia de un cliente a la espera depende de muchos factores que resulta imposible enumerar de forma exhaustiva, incluso en un análisis introspectivo se puede apreciar que nuestra propia tolerancia no es rígida y se ve afectada por condiciones del ambiente, congestión del sistema, temperatura, urgencia, etc.
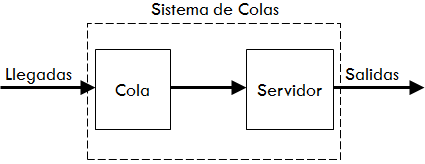
Una descripción general de la estructura de los modelos que representan lo que sucede en un proceso o línea de espera es la siguiente:
-
Clientes con una fuente de entrada (población finita o infinita). Una población finita se refiere a un conjunto limitado de clientes que usarán el servicio y en ocasiones formarán una línea. Por el contrario una población infinita es lo bastante grande en relación con el sistema de servicio.
-
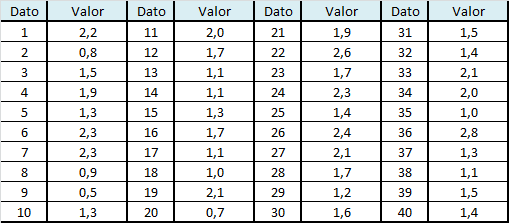
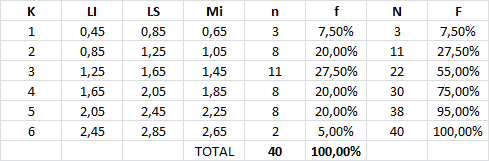
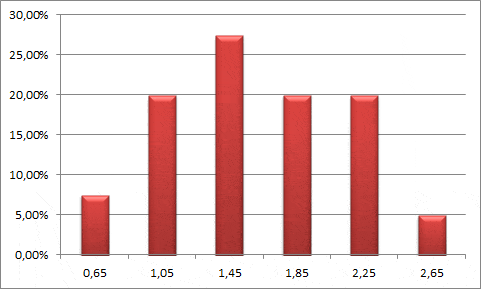
Clientes entran al sistema y se unen a una cola (tiempo entre llegada de clientes). Por lo general se supone que el tiempo entre llegada de clientes se distribuye de forma exponencial. No obstante se puede corroborar lo anterior a través de un ajuste de curva para lo cual se puede utilizar software estadístico como Easyfit.
-
Se proporciona el servicio (tiempos de servicio) por un servidor (uno y/o múltiples servidores) a un miembro de la cola, según una disciplina de servicio (disciplina de la cola). La disciplina de la cola más común es FIFO, es decir, se atiende por orden de llegada.
-
El cliente sale del sistema.
En este contexto uno de los escenarios más sencillo para el análisis es aquel donde existe una fase de servicio, un único servidor, con una fuente de entrada infinita y una longitud permisible de la fila ilimitada.
Ley de Little
Un importante resultado matemático es el demostrado por John Little en 1961, el cual relaciona las siguientes variables:
L : Número promedio de clientes en un sistema
W : Tiempo promedio de espera en un sistema
λ : Número promedio de clientes que llegan al sistema por unidad de tiempo
Luego la Ley de Little establece que el número promedio de clientes en un sistema (L) es igual a la tasa promedio de llegada de los clientes al sistema (λ) por el tiempo promedio que un cliente esta en el sistema (W).
La fórmula es válida para sistemas y para subsistemas, es decir:
Donde Lq es el número promedio de clientes que esperan en la fila y Wq el tiempo promedio que un cliente espera en la fila. Adicionalmente µ representa el ritmo del servicio o capacidad del sistema.
Ejemplo Ley de Little
Un pequeño banco está considerando abrir un servicio para que los clientes paguen desde su automóvil. Se estima que los clientes llegarán a una tasa promedio de 15 por hora. El cajero que trabajará en la ventanilla puede atender a los clientes a un ritmo promedio de uno cada tres minutos. Suponiendo que el patrón de llegadas es Poisson y el patrón de servicios es Exponencial, encuentre:
La utilización promedio del cajero:
El número promedio de clientes en la línea de espera es:
El número promedio de clientes en el sistema:
El tiempo promedio de la espera en la fila:
El tiempo promedio de espera en el sistema:
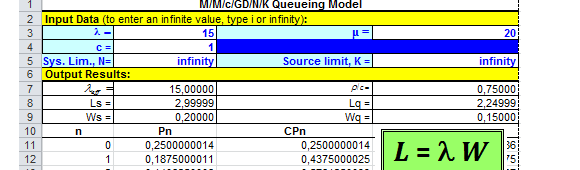
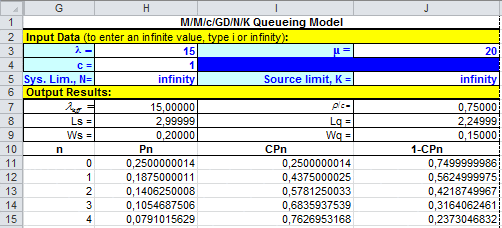
En el libro de Investigación de Operaciones de Hamdy Taha se puede encontrar un archivo en formato Excel que permite automatizar este tipo de cálculos y que facilita el análisis de las líneas de espera. El archivo lo puedes descargar aquí: Formulas Sistemas de Espera.
Para la utilización de la planilla se deben completar los datos de entrada (Input Data) y se obtienen automáticamente los resultados que son consistentes con lo detallado anteriormente.
El ejemplo que hemos presentado ha sido obtenido del Libro de Administración de Operaciones duodécima edición de los autores Chase, Jacobs y Aquilano el cual puede ser adquirido a través del siguiente enlace: