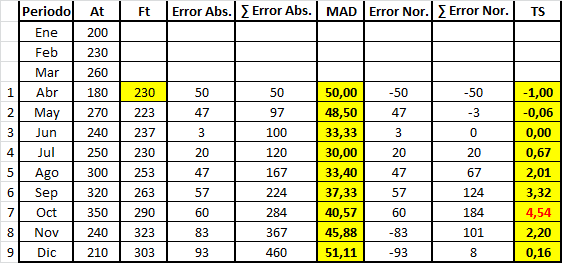
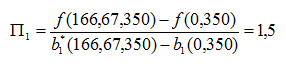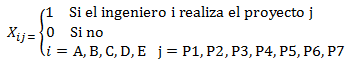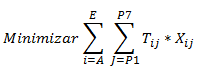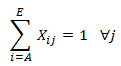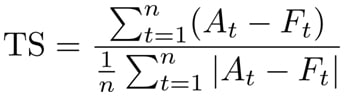El Precio Sombra de una restricción en Programación Lineal indica cuánto cambia el valor de la función objetivo (óptimo) ante una variación marginal del lado derecho de una restricción. Se asume que el resto de los parámetros del modelo permanecen constantes. De antemano es conveniente señalar que el Precio Sombra puede ser positivo, cero o negativo y en el Blog iremos discutiendo estos distintos escenarios.
Para obtener los Informes de Sensibilidad de un modelo de Programación Lineal se puede hacer uso de herramientas computacionales como Solver de Excel, sin embargo, en esta oportunidad nos enfocaremos en el cálculo del precio sombra de una restricción en forma gráfica, lo que nos ayudará más adelante a entender los conceptos que fundamentan los resultados de Solver.
Cálculo del Precio Sombra de una Restricción con el Método Gráfico
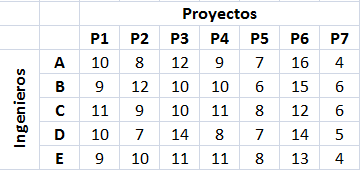
A continuación calcularemos el precio sombra de una restricción del siguiente modelo de Programación Lineal:
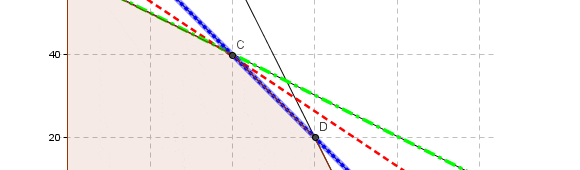
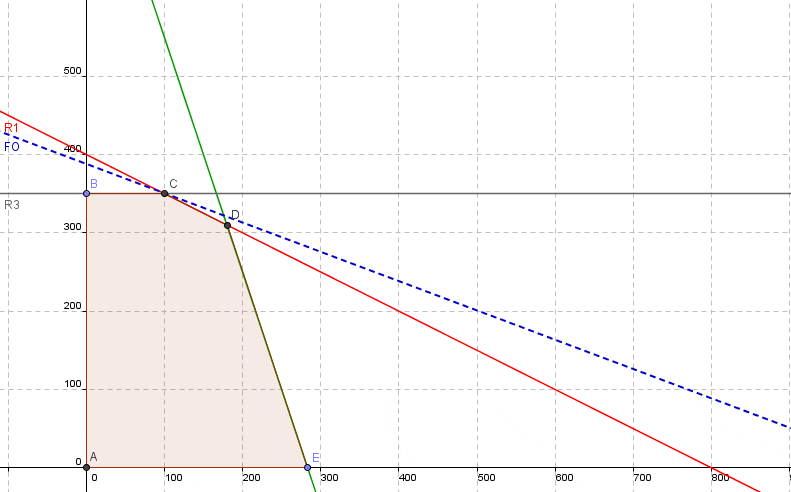
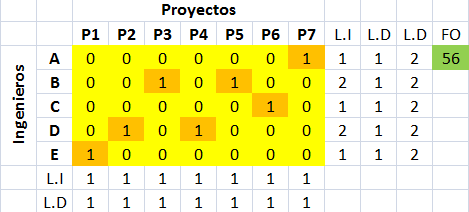
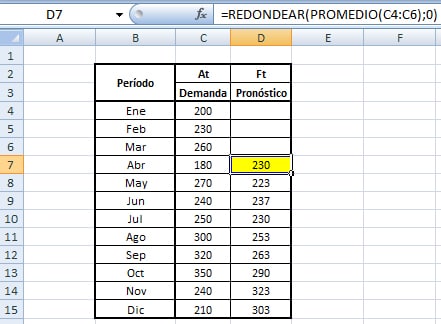
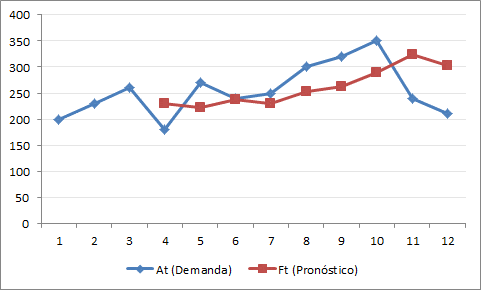
La solución óptima de este modelo es X=100 e Y=350 con valor óptimo V(P)=3.100 según su resolución gráfica con Geogebra o su resolución con Solver de Excel. El siguiente diagrama muestra la solución óptima obtenida gráficamente en el vértice C, que corresponde a la intersección de la restricción 1 (R1: color rojo) y la restricción 3 (R3: color gris), siendo ésta una solución básica factible óptima.
Supongamos que deseamos saber cuánto cambiará el valor óptimo (respecto a su valor actual) si aumenta en una unidad el lado derecho de la restricción 1 pero sin resolver nuevamente el problema. El precio sombra nos permite dar respuesta a dicha interrogante y permite anticipar el nuevo valor óptimo ante una variación marginal del lado derecho de una restricción.
Un variación marginal de un lado derecho implica que la nueva solución óptima se seguirá encontrando con las actuales restricciones activas, es decir, aquellas que se cumplen en igualdad en el óptimo (esto es se conserva la base óptima).
En el caso de la restricción 1 si aumentamos su lado derecho, ésta se desplazará en forma paralela hacia arriba. Si buscamos garantizar que la nueva solución óptima aún se encontrará con R1 y R3 activas llegaremos al vértice donde actualmente se interceptan la R2 y R3 que corresponde a la coordenada X=166,67 e Y=350 (ésta será la máxima variación).
En forma análoga si disminuimos el lado derecho de la restricción 1 y buscamos mantener R1 y R3 activas en el nuevo óptimo, el último punto donde se garantiza esto es el vértice B cuyas coordenadas son X=0 e Y=350 (ésta será la menor variación). Con esta información calculamos el precio sombra de la restricción 1:
Este precio sombra es válido si el lado derecho de la restricción 1 (actualmente b1=1.600) varía entre [1.400,1.733,33]. Por ejemplo, si el lado derecho de R1 aumenta de 1.600 a 1.700 el nuevo valor óptimo será V(P)=3.100+100*1,5=3.250. Análogamente si el lado derecho de R1 disminuye de 1.600 a 1.550 el nuevo valor óptimo será V(P)=3.100-50*1,5=3.025. (Se recomienda corroborar estos resultados gráficamente con TORA o IORTutorial). Notar que si la variación del lado derecho de la restricción 1 está por fuera del intervalo [1.400,1.733,33], no se puede utilizar el precio sombra para predecir cuál será el nuevo valor óptimo.
En un próximo análisis complementaremos el cálculo del precio sombra de las restricciones 2 y 3 en conjunto con otros Análisis de Sensibilidad en la resolución de modelos de programación lineal. Hasta entonces!
se define como 
donde 
es la demanda real u observada en el período t y 
es la demanda pronosticada para el mismo período.
, entonces tenemos una subestimación de la demanda real de una magnitud de 50 unidades.
, por tanto en este caso tenemos una sobrestimación de la demanda real de una magnitud de 100 unidades.
