línea de ensamble Archivos - Gestión de Operaciones

Qué es Just in Time (JIT o Justo a Tiempo)

La filosofía de manufactura Just in Time (conocido simplemente por su acrónimo JIT en inglés o en su traducción al español Justo a Tiempo) postula que se debe producir solo lo que sea necesario, en la cantidad que sea necesaria y en el momento que sea necesario. Lo anterior establece como un imperativo de cualquier negocio que aspira ser de Clase Mundial (World Class) la reducción de capital inmovilizado con el correspondiente impacto en la eficiencia de los procesos y la reducción de costos.

Qué hace el Just in Time (JIT)

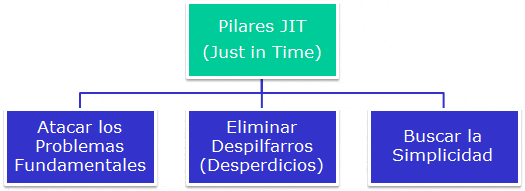
Just in Time (Justo a Tiempo) se basa sobre 3 pilares u objetivos básicos:

Atacar los problemas fundamentales
Eliminar despilfarros (desperdicios)
Buscar la simplicidad

1. Atacar los Problemas Fundamentales

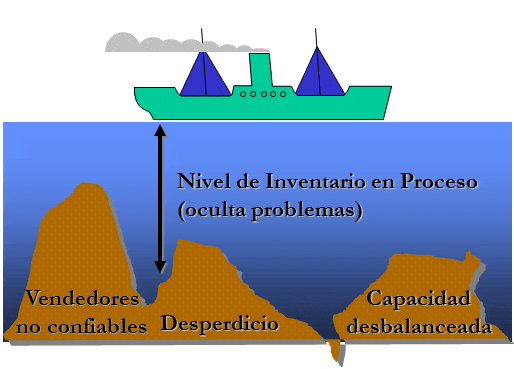
Consiste en atacar las causas fundamentales de los problemas, resolviendo éstos sin encubrirlos. El enfoque anterior se puede representar a través de una analogía denominada “mar de las existencias” que indica básicamente que el nivel de inventario o existencias suele ocultar problemas en los procesos.

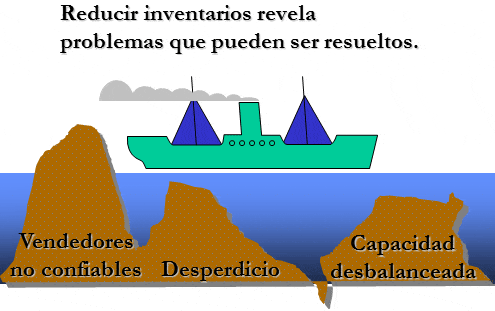
El nivel del mar representa las existencias o inventario y las operaciones de la empresa se visualizan como un barco. Cuando una empresa intenta bajar el nivel del mar, en otras palabras, reducir el nivel del inventario, descubre rocas, es decir, problemas.

El solo hecho de identificar los problemas no garantiza por cierto que estos se resuelvan, sin embargo, se cimientan las bases para poder enfrentar las causas que lo generan (acá se puede hacer uso de metodologías complementarias de la Gestión de Calidad como el Diagrama de Ishikawa y Diagrama de Pareto). De esta forma se deba atacar las causas de los problemas que causan las ineficiencias y no sólo concentrarse en los síntomas o efectos.

En palabras del ingeniero japones Taiichi Ohno, precursor de la filosofía Just in Time (JIT) al interior del sistema de producción del fabricante de automóviles Toyota.

Si se ha entendido bien lo que es el control de la producción, entonces es innecesario el control de inventarios.

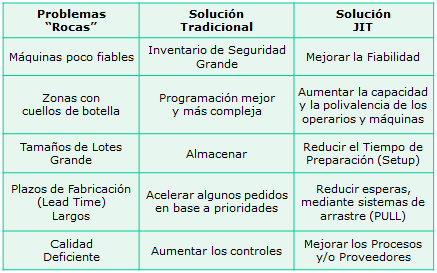
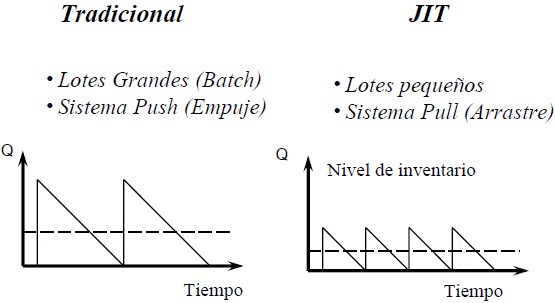
De esta forma y en consecuencia a lo discutido anteriormente se pueden establecer diferencias entre el enfoque Tradicional y el enfoque de Just in Time JIT:

2. Eliminar Despilfarros (Desperdicios)

El desperdicio (waste en inglés) se refiere a toda inversión de costo, tiempo, material, mano de obra o recursos aplicada en exceso versus lo mínimo indispensable para ofrecer un Producto y/o Servicio que exceda cualitativa y cuantitativamente las expectativas del cliente.

De esta forma en la manufactura Justo a Tiempo (JIT) el énfasis debe estar en eliminar todas aquellas actividades que no añaden valor al producto con lo que se reduce costos, mejora la calidad, reduce los plazos de fabricación (lead time logístico) y aumenta el nivel de servicio al cliente (que se puede medir cuantitativamente a través de indicadores como Instock, Fill-rate, entre otros).

Algunos ejemplos de los tipos de desperdicios más comunes son:

1. Sobreproducción
2. Tiempo de Espera
3. Transporte
4. Inventario
5. Proceso inadecuado (reprocesamiento)
6. Movimientos innecesarios
7. Defectos en Productos

Luego una forma de poder enfrentar los desperdicios es a través de un enfoque sistémico como el propuesto en JIT que se basa en los siguientes criterios:

Hacer el producto y/o prestar el servicio bien en la primera oportunidad
El operario asume la responsabilidad de controlar, es decir, el operario trabaja en autocontrol
Garantizar el buen desempeño del proceso mediante el Control Estadístico de Procesos (CEP)
Analizar y prevenir los riesgos potenciales que hay en un Proceso
Reducir stocks (Inventarios) al máximo

De esta forma se pueden establecer metas ambiciosas que sean consistentes con el objetivo de eliminar los desperdicios. Entre ellas destacan:

?Cero defectos (Seis Sigma)
?Cero Tiempo de Preparación (Setup Time)
?Cero Inventarios
?Cero Manejo de Materiales
?Cero Lead Time (Plazos)
?Tamaño de Lote Unitario (Q* bajos)
?Productos que satisfagan las necesidades (Calidad)

3. Buscar la Simplicidad

Por regla general los enfoques de producción simples están asociados a una gestión más eficaz. El primer tramo del camino hacia la búsqueda de la simplicidad abarca 2 zonas:

Flujo de Material
Control de las Líneas de Flujo

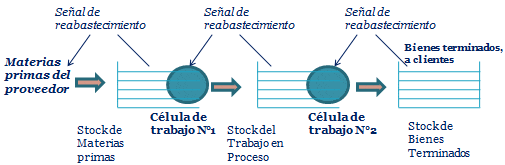
Un enfoque simple respecto al flujo de material es eliminar las rutas complejas y priorizar líneas de flujo más directas, en lo posible unidireccionales. Otra alternativa es agrupar los productos en familias que se fabrican en una línea de flujo, con lo que se facilita la gestión en células de producción (celdas de manufactura).

De forma complementaria la simplicidad del Justo a Tiempo (JIT) también se aplica al manejo de las líneas de flujo. Un ejemplo de ello es el sistema Kanban, en el que se arrastra el trabajo (sistema Pull o Jalar que consiste en producir sólo lo necesario, tomando el material requerido de la operación anterior).

En resumen el enfoque Just in Time (JIT) o Justo a Tiempo se basa en el control físico del material para identificar los desperdicios y forzar su eliminación. JIT es una filosofía propia de la Ingeniería Industrial que consiste en la reducción de desperdicio (actividades que no agregan valor) es decir todo lo que implique sub-utilización en una Cadena de Suministro desde compras hasta producción.

Requisitos del Just in Time (JIT)

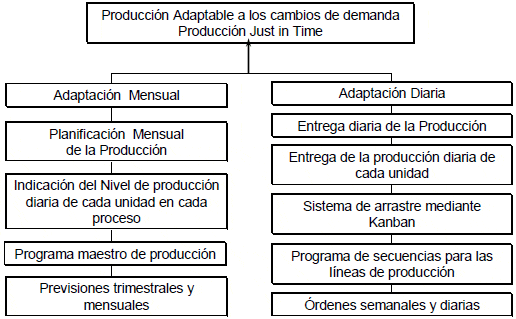
1. ?Nivelado de la Producción: consiste en adaptar los niveles de producción a los cambios que se observan en el comportamiento de la demanda. De esta forma se busca que el Plan Maestro de la Producción sea altamente sensible y adaptable a la aleatoriedad de la Demanda, disminuyendo al mínimo la producción de unidades innecesarias.

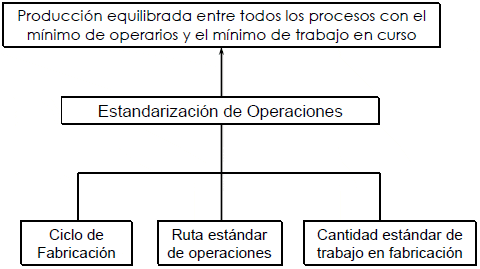
2. Estandarización de Operaciones: se busca que los niveles de producción sean equilibrados en todos los procesos utilizando la cantidad mínima de operaciones y recursos, además de minimizar el trabajo en curso (WIP).

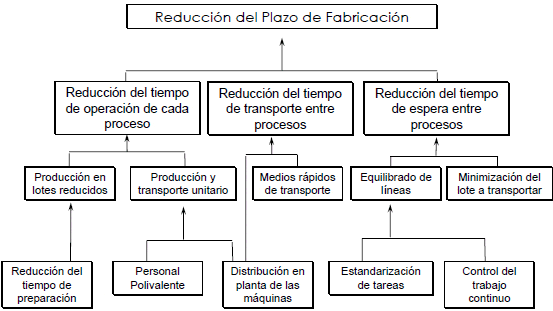
3. ?Reducción del Tiempo de Fabricación: consiste en implementar un conjunto de estrategias congruentes que apunten a la reducción de los tiempos requeridos para fabricar los productos. Destaca la reducción del tiempo de operación en cada proceso, reducción de los tiempos de transporte y la reducción de los tiempos de espera o tiempos muertos entre procesos (esto último, por ejemplo, a través del Balance de una Línea de Ensamble).

4. ?Reducción del Tiempo de Preparación: usualmente se asume el setup como irreducible y dado, en efecto en las fórmulas tradicionales de Lote Económico (EOQ) se observa un trade off entre los costos de emisión de pedidos y los costos de almacenamiento de inventario. En este sentido la filosofía JIT reconoce la importancia de reducir el tiempo de emisión o preparación al mínimo posible.

De esta forma bajos setups y lotes pequeños llevan naturalmente a bajos lead times, ?acortando el horizonte de planificación y el pronóstico es mas preciso. Adicionalmente ?el sistema puede cambiar rápido para atender un cambio en la demanda, aumentando la flexibilidad del sistema.

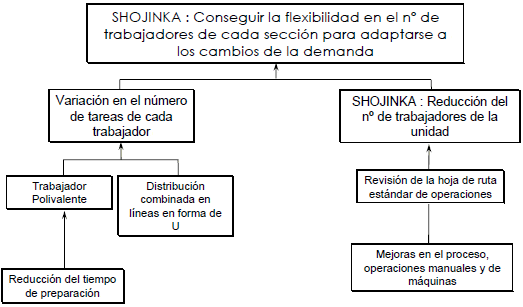
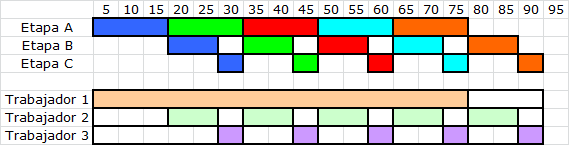
5. Distribución en Planta y Polivalencia: se busca privilegiar a través de la distribución de planta o layout y un esquema de organización del trabajo colaborativo y polivalente, de modo de aprovechar al máximo la disponibilidad de tiempo y capacidades de los trabajadores.

Consistente con esta estrategia se puede utilizar el tiempo sobrante (disponible) para múltiples propósitos con fines productivos entre los que destacan: transferencia de trabajadores a otras líneas, disminución de horas extraordinarias, reuniones de círculos de calidad, prácticas en mejora de programación, mantenimiento y reparación de máquinas, mejora de herramientas e instrumentos, etc.

Cómo implementar Just in Time (JIT) en la Empresa

?La adopción del sistema de manufactura Justo a Tiempo o JIT debe nacer como parte de una Planificación Estratégica, es decir, con una mirada de largo plazo que sea consistente con la ?adaptación de los requisitos y principios del JIT, bajo un ambiente de control y evaluación constante.

En este contexto implementar Just in Time (JIT) no es sencillo y se debe lidear con un importante numero de obstáculos que dificultan su adopción, entre los que destacan:?

Compromiso de la Directiva y Trabajadores
Disciplina de Trabajo
Redistribución de la Planta
Relación con los Proveedores

Por tanto no se deben hacer falsas expectativas esperando resultados a corto plazo.

En relación a aquellas empresas que se enfrentan por primera vez a la implementación de un sistema JIT se recomienda la utilización de un proyecto piloto que cumpla con los siguientes requisitos:

No debe ser un producto nuevo
El proceso debe ser conocido
No se debe escoger un producto crónico o problemático
No se debe escoger un producto con atraso para su entrega

De esta forma se pueden acotar los riesgos asociados a una deficiente implementación.

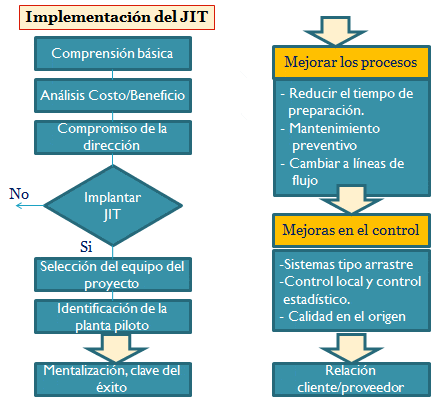
Finalmente en relación a la metodología de implementación se identifican 5 fases secuenciales que dada la evidencia empírica son adecuadas para la ejecución del JIT:

?Primera Fase: Educación (clave)
?Segunda Fase: Distribución y Polivalencia
?Tercera Fase: Mejoras en el proceso
?Cuarta Fase: Mejoras en el control
Quinta Fase: La ejecución

Just in Time (JIT) o Justo a Tiempo orienta a los procesos para que éstos funciones de forma correcta, correctamente la primera vez.

Cálculo del Costo de Mano de Obra por unidad de Producto

Un aspecto clave en todo proceso productivo es estimar los costos asociados a la fabricación de los distintos productos el cual esta compuesto por una sumatoria de distintos costos asociados al abastecimiento de materias primas, energía, insumos y servicios generales, mano de obra, etc. En este contexto en el siguiente artículo discutiremos 2 enfoques para el cálculo del costo de mano de obra (trabajo) por unidad de producto el cual entrega resultados disimiles.

Ejemplo Cálculo del Costo de Mano de Obra por unidad de Producto

Consideremos un proceso simple de fabricación a inventario (make to stock) que consta de 3 etapas secuenciales según se detalla en el siguiente diagrama de procesos y donde en cada etapa trabaja un trabajador que recibe un salario de US$12 la hora.

La capacidad del proceso es de 4[unidades/hora] lo cual esta dado por la Etapa A (cuello de botella), un tiempo de ciclo promedio de 15[minutos/unidad] o equivalentemente 1/4[hora/unidad] y un tiempo de flujo de 30[min]. Una descripción de cómo obtener estos indicadores se puede consultar en el artículo Cálculo del Tiempo de Ciclo, Capacidad de Producción y Tiempo de Flujo de una Línea de Ensamble.

Un enfoque de cálculo para el costo de la mano de obra por unidad de producto es considerar el tiempo de flujo, es decir, el tiempo mínimo que una unidad de producto tarda en pasar por el sistema (etapas A, B y C). En este sentido si el costo de una hora de trabajo es de US$12, entonces 30[minutos] (o 1/2[hora]) cuesta US$12*0,5=US$6,0.

Una alternativa al procedimiento anterior es considerar la capacidad del proceso para prorratear los costos que se incurren cada hora por concepto del trabajo. De esta forma el costo unitario es 12*3[US$/hora]/4[unidades/hora]=9[US$/unidad].

Las diferencias en los resultados alcanzados para los 2 procedimientos se debe al tiempo ocioso o tiempo muerto. En efecto resulta ser un escenario más realista el considerar que se incurre en un costo de US$36 por cada hora (por concepto de salarios) independiente de la utilización de los trabajadores. La siguiente Carta Gantt da cuenta de esta situación donde se puede observar que en particular los trabajadores de las Etapas B y C tienen tiempos muertos de 5 y 10 minutos, respectivamente, por cada unidad de producto terminado. No obstante, al considerar la capacidad del proceso en el cálculo del costo de la mano de obra se asume que el sueldo por hora se paga a todo evento.

Cálculo del Tiempo de Ciclo, Capacidad de Producción y Tiempo de Flujo de una Línea de Ensamble

Calcular los indicadores básicos de desempeño de un proceso productivo como lo es el tiempo promedio de ciclo, la capacidad máxima de producción y el tiempo de flujo de una unidad de producto en un proceso con actividades que se realizan en forma simultanea, puede resultar ser un trabajo más complejo en comparación a un proceso que sólo considera un conjunto de actividades que se desarrolla de forma secuencial. En este contexto se presenta un ejemplo de una empresa construcción de robots que trabaja con 3 lineas de ensamble que arman el Software, Hardware y Piezas de Conexión respectivamente, para luego ser unidas en una última linea de 3 tareas (I, J y K). El siguiente diagrama muestra las tareas necesarias para la construcción de producto final y las capacidades de cada tarea medidas en [u/hr].

A continuación se presentan algunas preguntas típicas del análisis cuantitativo de procesos que nos ayudarán a comprender de mejor forma el cálculo de los indicadores anteriormente individualizados.

1. Analizar el proceso indicando el tiempo de flujo del proceso, el tiempo de ciclo promedio, la tarea que es cuello de botella y la capacidad total del proceso.

El tiempo de flujo es la suma de la linea más larga junto con la linea de producción común, es decir, 19,3[min] + 11,6[min] = 30,9[min] (aproximado). Notar que esto implica que ningún producto final podrá ser terminado en un tiempo menor a 30,9[min], esto es, el tiempo que pasa desde que se inicia su procesamiento hasta que termina su ejecución en la etapa K.

Adicionalmente las capacidades de las actividades individuales en $[u/hr]$ han sido transformadas a sus tiempos de ciclo asociados, por ejemplo, si la actividad A tiene una capacidad de $15[u/hr]$ esto implica que su tiempo de ciclo es $4[min/u]$ (también sería válido decir que el tiempo de ciclo es $\frac{1}{15}[hr/u]$ ). Finalmente es sencillo notar que el cuello de botella son las tareas B y D, siendo la capacidad del sistema de $12[u/hr]$ .

2. Si pudiera agregar alguna tarea en paralelo (sin importar qué tarea sea), ¿Cuál sería? ¿Cuál es el nuevo cuello de botella?.

Si se pudiera agregar otra actividad naturalmente la tendríamos que agregar al cuello de botella, en este caso a las actividades B o D. Con esto el tiempo de flujo no cambia. El siguiente diagrama muestra el caso de incorporar una actividad D adicional:

La capacidad del proceso se mantiene en $12[u/hr]$ debido a que se conserva el cuello de botella de las actividades B. Ahora si se pudiera al diagrama anterior agregar una actividad B adicional en paralelo, entonces la capacidad del proceso estaría dada por las actividades C y J ( $13[u/hr]$ ).

Problema de Producción y Ensamblaje resuelto con el Método Simplex

El siguiente problema de Programación Lineal fue enviado por uno de nuestros lectores desde Puerto Rico. Consiste en determinar la política óptima de producción y ensamblaje de una empresa que se dedica a fabricar componentes para computadoras. A continuación los detalles de dicho problema el cual luego de su formulación (definición de las variables de decisión, función objetivo y restricciones) será resuelto a través del Método Simplex:

Problema de Producción y Ensamblaje

Una pequeña compañía fábrica tres componentes electrónicos de computadoras. Componente A requiere 2 horas de fabricación, 1 hora de ensamblaje y 1 hora de finalización; Componente B requiere 3 horas de fabricación, 1 hora de ensamblaje y 1 hora de finalización; y el Componente C requiere 2 horas de fabricación, 2 horas de ensamblaje y 1 hora de finalización. La compañía tiene a lo sumo 1.000 horas de labor en la fabricación, 800 horas de labor en el ensamblaje y 100 horas de finalización disponibles cada semana. Las ganancias de cada componente A, B y C, son $7, $8 y $10, respectivamente.

¿Cuántos componentes de cada tipo debe la compañía fabricar cada semana de manera que pueda maximizar sus ganancias? ¿Cuál es la ganancia máxima?. Resuelva el problema de Programación Lineal utilizando el Método Simplex.

Sea $x_{1}, x_{2}, x_{3}$ la cantidad de unidades a producir semanalmente del Componente A, B y C, respectivamente, un modelo de Programación Lineal que permite abordar el problema anterior es:

De modo de resolver el modelo a través del Método Simplex llevamos el mismo al formato estándar, agregando $x_{4}, x_{5}, x_{5}$ como variables de holgura de las restricciones 1, 2 y 3, respectivamente (fabricación, ensamblaje y finalización).

Lo que da origen a la siguiente tabla inicial del método:

Por el criterio del costo reducido más negativo ingresa a la base la variable $x_{3}$ . Luego calculamos el mínimo cuociente en dicha columna obteniendo: $Min \begin{Bmatrix}{\frac{1.000}{2}, \frac{800}{2}, \frac{100}{1}}\end{Bmatrix}=100$ , el pivote está en la fila 3 y en consecuencia $x_{6}$ deja la base. Se realiza entonces una iteración:

Notar que luego de una iteración las variables no básicas $x_{1}, x_{2}, x_{6}$ tienen costos reducidos mayores a cero, además las variables básicas cumplen con las condiciones de no negatividad, a saber, $x_{3}=100, x_{4}=800, x_{5}=600$ , lo que corresponde a una solución básica factible óptima. En consecuencia se propone producir exclusivamente 100 unidades del Componente C lo que reporta un valor óptimo (ganancia máxima) de $1.000.

Ejemplo del Balance de una Línea de Ensamble utilizando la Regla del Candidato Más Extenso

Una línea de ensamble consiste en un ensamble progresivo que esta asociado por algún tipo de aparato o dispositivo que maneja los materiales, donde el equipo o los procesos de trabajo están ordenados siguiendo los pasos progresivos de la fabricación del producto. Los productos que se producen parcial o totalmente en las líneas de ensamble incluye juguetes, electrodomésticos, automóviles, aviones, armas de fuego, etc. En consecuencia casi todo producto que tiene varias partes y que se producen en volúmenes importantes utiliza las líneas de ensamble en alguna medida.

Equilibrar o balancear una línea de ensamble depende básicamente de la programación, no obstante dicha programación por lo general tiene un impacto directo en la distribución o layout de la planta.

En este contexto el problema del balanceo de la línea de ensamble consiste en asignar todas las tareas a una serie de estaciones de trabajo de modo que cada una de ellas no tenga más de lo que puede hacer en el tiempo de ciclo de dicha estación y que el tiempo inactivo de todas las estaciones de trabajo sea el menor posible.

A continuación se presenta un ejemplo de un proceso que consta de 8 actividades o tareas, el cual corresponde a una línea de ensamble que opera 8 horas al día con una producción deseada de 240 unidades diarias. La siguiente tabla contiene información acerca de los tiempos de la tarea de este producto y las relaciones de precedencia:

Se requiere un dibujo que represente el diagrama de precedencia. ¿Cuál es el tiempo del ciclo de la estación de trabajo?. A continuación balancee esta línea de ensamble utilizando la tarea de tiempo más largo.

El diagrama de precedencia que representa el proceso descrito anteriormente se presenta a continuación. Se puede observar, por ejemplo, que la tarea B tiene una duración de 80 segundos y es posterior a la tarea A que dura 60 segundos.

Luego es necesario determinar el Tiempo de Ciclo (C) que requieren las estaciones de trabajo a través de la siguiente fórmula:

En el ejemplo propuesto el proceso opera 8 horas al día (equivalente a 8[horas/día]*3.600[segundos/hora]=28.800[segundos/día]) con un nivel de producción deseado de 240 unidades. Dado lo anterior el Tiempo de Ciclo (C) es:

A continuación se requiere estimar el número mínimo de estaciones de trabajo (Nt) que, en teoría, se requiere para cumplir el límite del tiempo de ciclo de la estación de trabajo a través de la siguiente fórmula (en caso de obtener un resultado fraccionario se debe redondear al entero superior más cercano).

Notar que el numerador del cálculo anterior corresponde a la sumatoria de los tiempos de las 8 tareas (60+80+20+50+90+30+30+60=420[segundos]). Con ello se espera (en teoría) que sean necesarias 4 estaciones de trabajo y se procede con la configuración de las mismas utilizando como criterio el tiempo más largo o candidato más extenso: Los resultados se resumen en la siguiente tabla:

Por ejemplo la estación 1 considera la tarea A que tiene un tiempo de 60 segundos y dado que el tiempo de ciclo es de 120 segundos el tiempo remanente no asignado también será de 60 segundos. Luego de A siguen las tareas B, C y D (según el diagrama de precedencia) no obstante se descarta B dado que su tiempo es de 80 segundos que es superior al tiempo remanente no asignado, por tanto los candidatos factibles para acompañar a la tarea A en la estación 1 son las tareas C o D. El criterio en este caso es seleccionar la tarea D dado que su tiempo es 50 segundos (mayor que los 20 segundos de C) lo que procura minimizar el tiempo inactivo de la estación de trabajo (que en este caso luego de asignar A y D a la estación de trabajo 1 es de 10 segundos).

Continuando con el procedimiento se determinan las tareas pertenecientes a la estación 2. En primer lugar se podría asignar B o C, no obstante se privilegia B por tener una mayor duración. Sin embargo, luego de asignar B la única tarea remanente viable es C así que se asigna a la estación 2 determinando que el tiempo remanente no asignado de dicha estación es de 20 segundos.

La estación 3 considera en primer lugar la asignación de la tarea E por el criterio del candidato más extenso o de mayor duración. Luego se asigna F con una duración de 30 segundos lo que permite que el tiempo inactivo de esta estación sea nulo. Finalmente la conformación de la estación 4 es trivial con G y H asignadas en ese orden. El siguiente diagrama representa el resultado final donde cada estación de trabajo se ha identificado con un color diferente para mayor claridad: