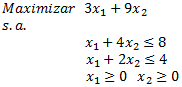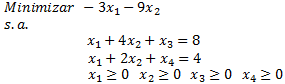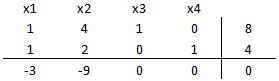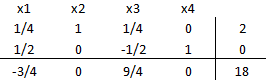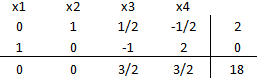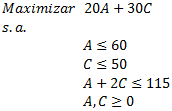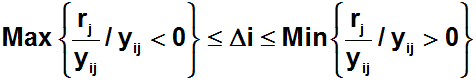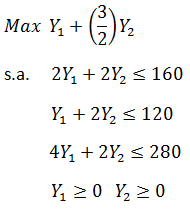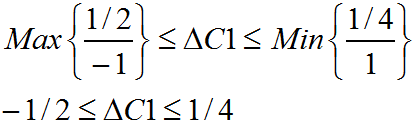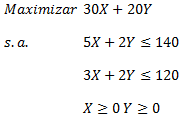En la aplicación del Método Simplex al hacer el cálculo del mínimo cuociente o condición de factibilidad, se puede romper un empate en la razón o cuociente mínimo en forma arbitraria. En este caso, al menos una variable básica será cero en la siguiente iteración, afirmándose en este caso que la nueva solución es degenerada. La implicancia práctica de dicha condición indica que el modelo tiene al menos una restricción redundante.
Solución Óptima Degenerada
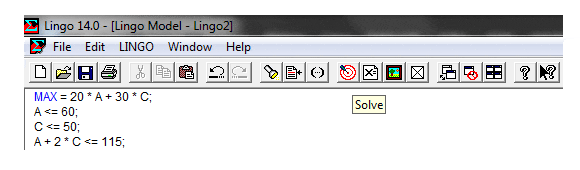
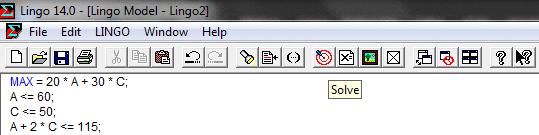
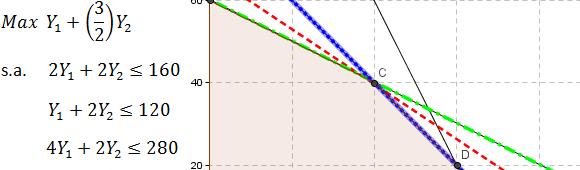
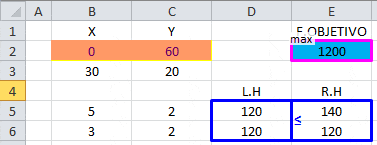
Consideremos el siguiente modelo de Programación Lineal el cual resolveremos a través del Método Simplex y que de forma complementaria representaremos gráficamente con Geogebra:
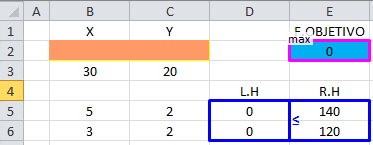
Llevamos el problema anterior a su forma estándar de minimización, agregando y
, como variables de holgura de las restricciones 1 y 2, respectivamente.
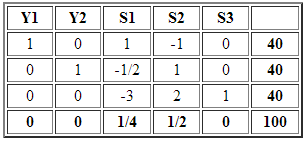
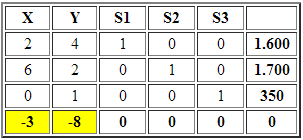
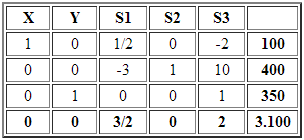
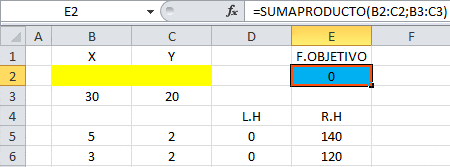
Que da origen a la siguiente tabla inicial del Método Simplex:
Para favorecer la rapidez de convergencia del algoritmo seleccionamos como la variable que ingresa a la base. A continuación calculamos el criterio de factibilidad (mínimo cuociente):
(al existir empate seleccionaremos arbitrariamente la variable
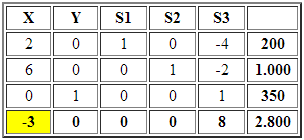
como aquella que deja la base. Luego se actualiza la tabla:
Ahora ingresa a la base. El criterio de factibilidad determina que:
deja la base. Se realiza entonces una nueva iteración:
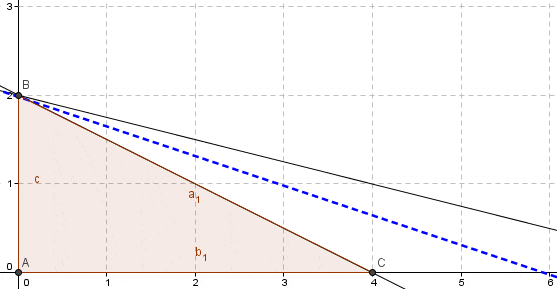
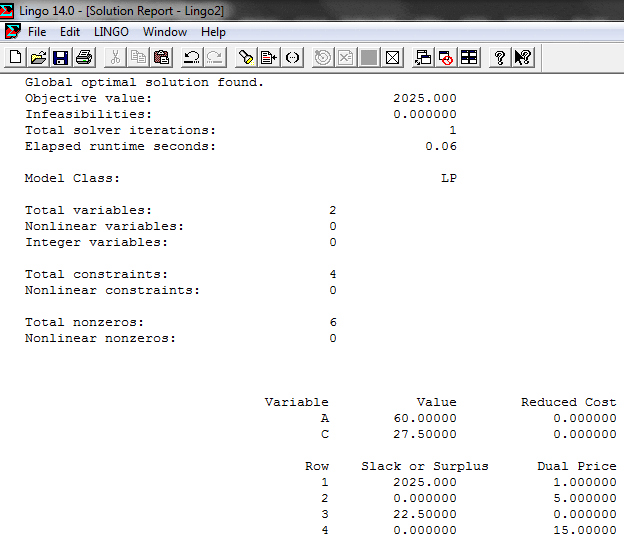
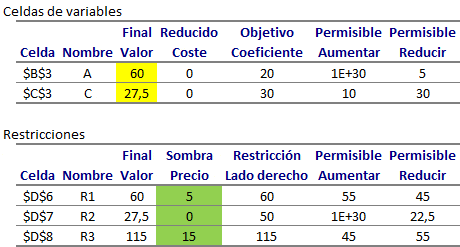
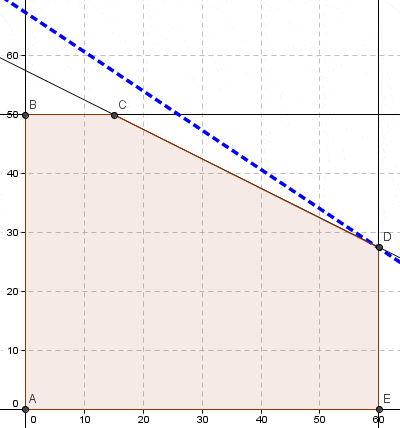
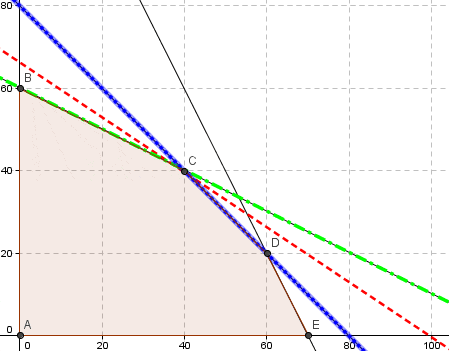
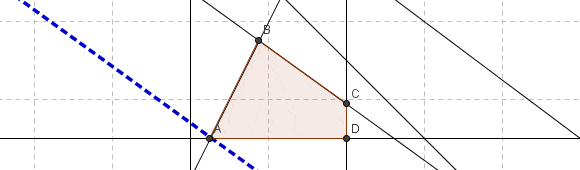
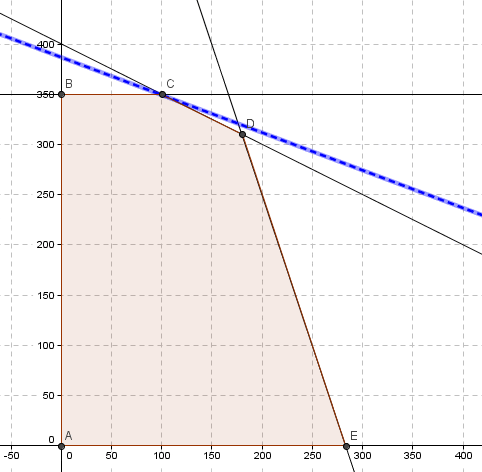
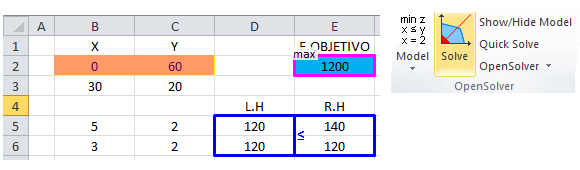
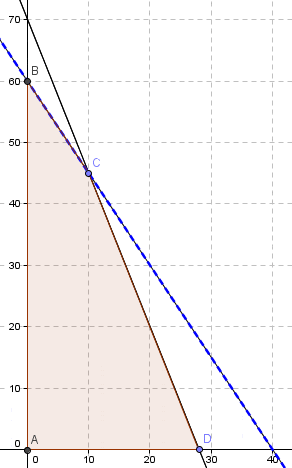
Se alcanza la solución óptima degenerada del problema lineal. Notar que . Como éste es un problema bidimensional, la solución está sobredeterminada y una de las restricciones es redundante tal como se corrobora en la representación gráfica:
En la práctica conocer que algunos recursos (como los asociados a una restricción) son superfluos puede ser valioso durante la implementación de la solución. Desde el punto de vista teórico, la degeneración tiene dos implicaciones: se genera el fenómeno de ciclos o círculos (es posible que el Método Simplex repita una serie de iteraciones sin mejorar el valor de la función objetivo, tal como se observo en el ejemplo anterior e incluso eventualmente nunca terminar los cálculos); el segundo aspecto teórico surge al examinar las iteraciones 1 y 2. Las dos, aunque difieren en la clasificación de las variables básicas y no básicas, producen valores idénticos para todas las variables y el valor objetivo ( ).