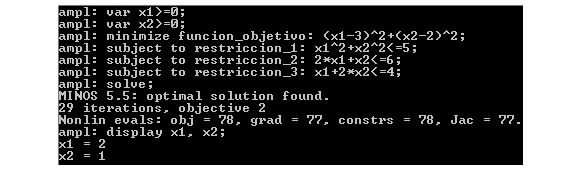
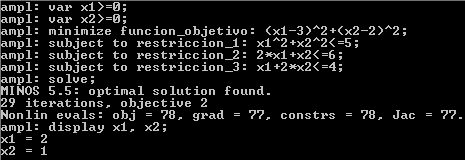
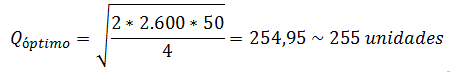Minientrada archivos - Gestión de Operaciones

Restricción con Precio Sombra Negativo en Programación Lineal

En Programación Lineal, el Precio Sombra se refiere a una tasa de cambio del valor óptimo ante una modificación marginal del lado derecho de una restricción, entendiendo como marginal una modificación que permita mantener las actuales restricciones activas para el problema (se conserva la base óptima). En este tipo de análisis se asume que el resto de los parámetros del modelo permanecen constantes.

En artículos anteriores hemos analizado Cómo calcular el Precio Sombra de una Restricción Gráficamente y en forma complementaria Cómo interpretar los Informes de Sensibilidad de Restricciones de Solver de Excel. Esto sin duda es una buena base conceptual para entender el significado del Precio Sombra de una restricción.

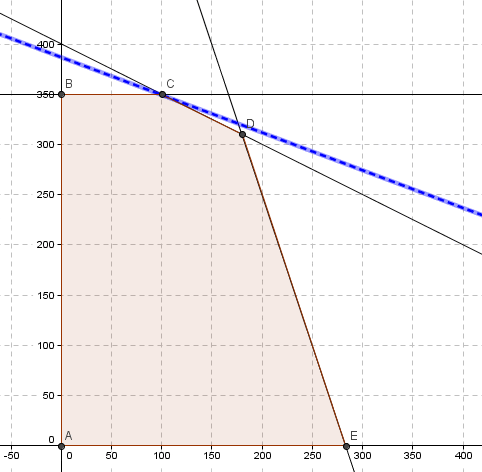
En esta oportunidad nos referiremos a una situación que a priori podría parecer anómala, pero que definitivamente no lo es: que una restricción asociada a un modelo de Programación Lineal tenga un Precio Sombra negativo.

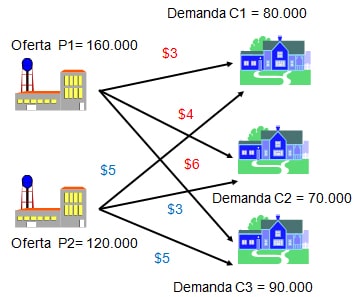
Para ilustrar este escenario utilizaremos nuevamente el Modelo de Transporte el cual se representa esquemáticamente a continuación:

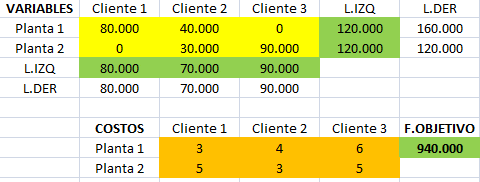
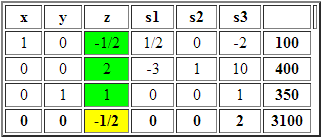
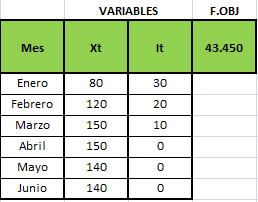
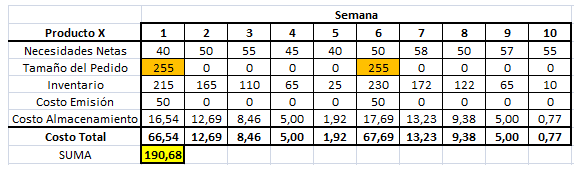
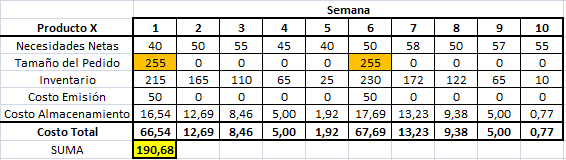
La resolución computacional de este modelo utilizando Solver de Excel se resume a continuación:

Notar que la Planta 1 tiene un exceso de capacidad de 40.000 unidades (diferencia entre su capacidad de 160.000 y las 120.000 unidades que despacha).

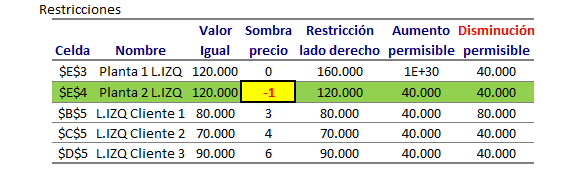
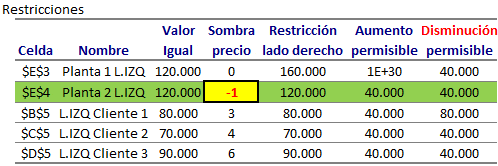
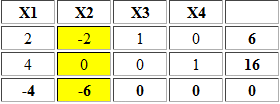
Por el contrario la Planta 2 funciona a máxima capacidad (despacha 120.000 unidades). El Informe de Sensibilidad de restricciones reporta lo siguiente:

La restricción de capacidad de la Planta 2 tiene un Precio Sombra negativo de magnitud -1. Esto significa que si se incrementa en una unidad la capacidad de la Planta 2 (a 120.001 unidades) el nuevo valor óptimo será 939.999.

Análogamente, cualquier cambio en la capacidad de la Planta 2 en el intervalo [120.000-40.000,120.000+40.000]=[80.000,160.000] generará una modificación del valor óptimo del problema proporcional al Precio Sombra de la restricción de capacidad de dicha planta.

Por ejemplo, si la capacidad de la Planta 2 aumenta a 130.000 unidades, el nuevo valor óptimo será:

$V(\bar{P})=V(P)+\Delta b\cdot \pi =940.000+(130.000-120.000)\cdot -1=930.000$

Por el contrario, si la capacidad de la Planta 2 disminuye a 110.000 unidades, el nuevo valor óptimo es:

$V(\bar{P})=V(P)+\Delta b\cdot \pi =940.000+(110.000-120.000)\cdot -1=950.000$

¿Por qué se produce este fenómeno?. Básicamente por una reasignación debido a que resulta ser relativamente más conveniente generar despachos desde la Planta 2 en comparación a la Planta 1 (que tiene capacidad ociosa y por tanto un Precio Sombra igual a cero).

7 Recursos Gratuitos para el estudiante de Investigación de Operaciones

En Internet existen recursos gratuitos valiosos para los estudiantes de los cursos de Investigación de Operaciones (conocido también como Investigación Operativa) que son de gran ayuda para complementar los conceptos tratados en el aula y la bibliografía. En el siguiente artículo ponemos en disposición de nuestros lectores algunos recursos que recomendamos:

1. Solver: Es sin duda la principal herramienta para resolver modelos de optimización de tamaño reducido utilizado por los alumnos de cursos de ingeniería. Este complemento de Excel se puede descargar desde el sitio web de Frontline en su versión comercial (Premium Solver Pro) para implementar modelos de mayor tamaño.

2. What’sBest!: Es la alternativa a Solver dado que funciona integrada en una planilla de cálculo (Excel). La interfaz es intuitiva y seguramente quién domine Solver no demorará mucho en aprender los elementos básicos de este programa. What’sBest! ha sido desarrollado por la empresa de software Lindo.

3. AMPL: Es un lenguaje de programación matemática que permite abordar la formulación y resolución de modelos de optimización de programación lineal, programación entera y programación no lineal (entre otros). Esta plataforma es popular para modelos de mayor complejidad que requieren para su resolución de algoritmos especializados.

4. GAMS: Es una herramienta de formulación matemática alternativa a AMPL que permite formular y resolver modelos de optimización de complejidad mayor.

5. NEOS Solvers: Es un portal que consolida una gran variedad de solvers (algoritmos) que permiten resolver distintas categorías de modelos de optimización formulados en un lenguaje matemático determinado (como AMPL y GAMS). El procedimiento es el siguiente: se selecciona un solver que permita resolver nuestro modelo (depende del lenguaje de programación matemática y el tipo de modelo), se sube el archivo del modelos (y/o datos) y se obtienen los resultados online.

6. Geogebra: Es un excelente programa que nos ayuda a graficar distintas formas geométricas y en particular resolver gráficamente modelos de optimización lineales o no lineales. Este programa se puede descargar gratuitamente e instalar en nuestro computador o alternativamente utilizar su aplicación web directamente sin necesidad de descargar el programa.

7. Método Simplex (ProgramacionLineal.net): Es una herramienta que permite resolver modelos de programación lineal a través del método simplex, mostrando paso a paso las respectivas iteraciones, solución óptima y valor óptimo.

8. Linear Programming: Versión en inglés de los principales artículos de este Blog que trata sobre la Investigación de Operaciones y en particular de la Programación Lineal, con recursos educativos y ejercicios resueltos.

Problema de Producción e Inventario resuelto con Solver de Excel

La Programación Lineal nos permite abordar distintos problemas de naturaleza real algunos de los cuales ya hemos tratado en artículos anteriores como el Problema de Transporte, el Problema de Mezcla de Productos y el Problema de la Dieta.

En el siguiente artículo analizaremos otra aplicación clásica conocida como el Problema de Producción e Inventario cuyas extensiones y variantes se pueden consultar adicionalmente en la categoría del Plan Maestro de la Producción.

El Problema de Producción e Inventario consiste básicamente en determinar una política de producción en el tiempo que permita satisfacer ciertos requerimientos de demanda, respetando las limitantes de producción y a un costo mínimo.

Este tipo de modelos se puede extender para varios productos, sin embargo, en esta oportunidad consideraremos un solo producto para su ilustración.

En este contexto, consideremos los siguientes antecedentes de producción que se presentan a continuación:

Luego, definimos el siguiente modelo de optimización lineal:

Supuesto: se dispone de un inventario inicial de 50 unidades, es decir, I0=50.

1. Variables de Decisión:

Xt: Unidades a producir en el mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)
It: Unidades a almacenar en inventario al final del mes t (t=1,..,6 con t=1 => Enero; t=6 => Junio)

2. Función Objetivo: Minimizar los costos de producción (destacados con color azul) y costos de inventario (destacados con color rojo) durante el período de planificación definido por:

60X1 + 60X2 + 55X3 + 55X4 + 50X5 + 50X6 + 15I1 + 15I2 + 20I3 + 20I4 + 20I5 + 20I6

De forma compacta (parametrica) se puede representar la función objetivo como:

$Minimizar\sum_{t=1}^{6}[C_{t}\cdot X_{t}+H_{t}\cdot I_{t}]$

Donde $C_{t}$ es el costo unitario de producción en el mes t (por ejemplo $C_{1}=60$ ) y $H_{t}$ es el costo unitario de almacenar unidades en inventario durante el mes t (por ejemplo $H_{1}=15$ )

3. Restricciones:

a) Satisfacer los requerimientos de demanda (conocida como restricción de Balance de Inventario).

Por ejemplo, el inventario disponible al final del mes de Enero será el resultado de la producción del mismo mes, más el inventario inicial (que se asume un dato, en este caso 50 unidades) menos la demanda satisfecha durante el mes de Enero.

X1 + 50 – I1 = 100 (Enero)
X2 + I1 – I2 = 130 (Febrero)
X3 + I2 – I3 = 160 (Marzo)
X4 + I3 – I4 = 160 (Abril)
X5 + I4 – I5 = 140 (Mayo)
X6 + I5 – I6 = 140 (Junio)

Notar que la restricción se Balance de Inventario impuesta para un producto se puede generalizar como: $X_{t}+I_{t-1}-I_{t}=d_{t}$ , donde $d_{t}$ representa la demanda estimada (parámetro) para el mes t.

b) Respetar la capacidad máxima de producción mensual (oferta).

Se establece que la oferta o producción máxima mensual no puede superar la capacidad de producción.

X1<=120 X2<=120 X3<=150 X4<=150 X5<=150 X6<=150

O simplemente $X_{t}\leq O_{t}$ donde $O_{t}$ es la capacidad de producción máxima del mes t (parámetro).

c) Condiciones de no negatividad.

De forma natural y dada nuestra definición cada variable de decisión debe ser no negativa.

Xt >= 0 It >= 0 Para todo t

El siguiente tutorial muestra cómo implementar este Modelo de Producción e Inventario correspondiente a la Programación Lineal en Solver de Excel:

La solución óptima se muestra a continuación con un valor óptimo de $43.450. Se puede apreciar que se producen en total 780 unidades entre Enero y Junio las cuales junto al inventario inicial de 50 unidades permiten satisfacer los requerimientos de demanda mensualmente.

¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Cómo detectar que un Problema es No Acotado con el Método Simplex

El Método Simplex es un algoritmo que nos permite resolver modelos de Programación Lineal que en ciertas ocasiones permite identificar casos excepcionales como infinitas soluciones óptimas o que el problema es no acotado. En este contexto el Método Simplex rescata las condiciones establecidas en el Teorema Fundamental de la Programación Lineal.

En la aplicación del Método Simplex, un problema no acotado se detecta cuando en una iteración cualquiera existe una variable no básica con costo reducido negativo y todos los elementos en la columna de dicha variable son negativos o cero. Es decir, no se puede seleccionar un pivote para determinar la variable que debe dejar la base.

Consideremos el siguiente modelo de Programación Lineal:

Si resolvemos gráficamente dicho modelo nos podemos percatar que éste es no acotado. Notar que el dominio de soluciones factibles (área sombreada o achurada) es no acotado dado que crece indefinidamente en la dirección de la variable X2.

Las curvas de nivel de la función objetivo crecen a su mayor tasa en la dirección del vector gradiente $\triangledown f(X_{1},X_{2})=(4,6)$ lo que indica que se podría desplazar indefinidamente en esa dirección y siempre interceptar el dominio de soluciones factibles.

¿Cómo podemos detectar esta situación (Problema No Acotado? utilizando el Método Simplex?

Para ello llevamos el modelo a su forma estándar, agregando X3 y X4 como variables de holgura de la restricción 1 y 2, respectivamente. Lo anterior define la siguiente tabla inicial del método:

Notar que X2 es la variable no básica con el costo reducido más negativo y siguiendo ese criterio debería ser aquella que ingresamos a la base. Sin embargo, no es factible hacer el criterio de factibilidad o mínimo cuociente debido a que los elementos en la columna de X2 son negativos o cero. En esta instancia ya se puede afirmar que el problema es no acotado.

Observación: Se puede verificar que si seleccionamos X1 como la variable que entra a la base y se aplica una iteración del Método Simplex se llegara a una conclusión similar a la presentada anteriormente.

Cantidad Económica de Pedido (EOQ) aplicada al MRP

En la aplicación del Plan de Requerimientos de Materiales (MRP) es necesario determinar una política de lotificación que establezca cuánto y cuándo pedir las partes y piezas necesarias para poder cumplir con una meta de producción del producto final o categoría superior. El objetivo es cumplir con dichos requerimientos y a la vez procurar los menores costos asociados a la gestión del inventario.

Una de las políticas de lotificación es la de Cantidad Económica de Pedido (EOQ) utilizada en la Gestión de Inventarios, que busca minimizar los Costos Totales del Inventario. Para ello se deben verificar los supuestos de este modelo, principalmente que la demanda (en nuestro caso necesidades netas) sea constante. No obstante, como es difícil encontrar una situación práctica donde los requerimientos sean fijos durante el tiempo, se flexibiliza este supuesto y se usa un promedio para poder estimar el valor de la demanda anual.

Ejemplo Lotificación EOQ en el Plan de Requerimientos de Materiales

Consideremos las necesidades netas para el Producto X en un período de 10 semanas. Adicionalmente asumiremos que el Costo de Emisión (S), es decir, el costo asociado a realizar cada pedido (independiente de su tamaño) es de $50 y que el Costo de Almacenar una unidad del Producto X en inventario durante un año es igual a $4 (H).

Un primer paso para aplicar la política de lotificación de la Cantidad Económica de Pedido (EOQ) es estimar un valor de la demanda anual para el producto. En este sentido la suma de las necesidades netas para las 10 semanas es igual a 500 unidades, lo que otorga un promedio de 50 unidades por semana. Si consideramos que un año tiene 52 semanas, entonces la demanda promedio anual es de 2.600 unidades.

Con esta información el tamaño de pedido que minimiza los costos de la gestión del inventario del Producto X es:

Luego desarrollamos la planificación de los pedidos en el tiempo para el período de 10 semanas, asumiendo que el tiempo de espera (lead time) es cero, es decir, tan pronto se emite un pedido se asume que este se recibe.

El primer pedido se realiza en la semana 1 por 255 unidades. Como la necesidad neta es de 40 unidades, nos quedan 215 unidades en inventario. El costo emisión es de $50 para la semana 1 (se realizó un pedido) y el costo de almacenamiento es de $16,54 (costo de almacenamiento semanal: $4/52*215 unidades).

Se puede observar que el inventario disponible luego del primer pedido es suficiente para satisfacer en forma íntegra la demanda hasta la semana 5.

En la semana 6 realizamos un segundo pedido por 255 unidades. Notar que en la semana 10 queda un inventario de 10 unidades a diferencia de lo que sucedería si aplicamos la política Lote a Lote.

Para acceder a un ejercicio detallado del Plan de Requerimientos de Materiales (MRP) donde se utiliza la política de lotificación Lote a Lote se recomienda revisar el artículo Ejemplo del Plan de Requerimientos de Materiales (MRP).

Es importante destacar que al utilizar la política de lotificación de la Cantidad Económica de Pedido (EOQ) no se garantiza necesariamente los menores costos de la gestión del inventario. En nuestro ejemplo el costo total es de $190,68 (si utilizáramos Lote a Lote el costo sería $500).