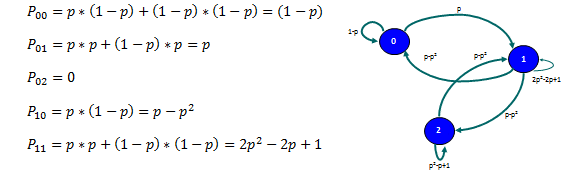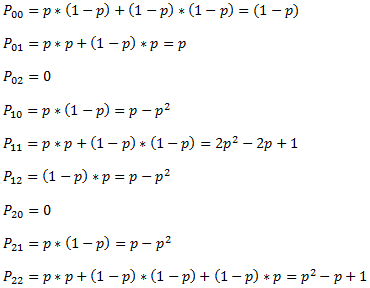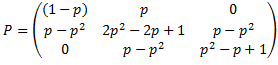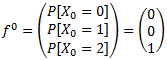En el siguiente artículo abordaremos la formulación de una Cadena de Markov en tiempo discreto, para la cual identificaremos la variable aleatoria que resulta de interés su análisis, los posibles estados que puede adoptar dicha variable en un periodo cualquiera y las probabilidades de transición en una etapa que se puede resumir en una matriz de transición de probabilidades conocida como matriz P. En dicho contexto consideremos el siguiente ejemplo:
Un individuo posee 2 paraguas los cuales emplea para ir de su casa al trabajo y viceversa (llevando uno a la vez). Si está en casa (oficina) al comienzo (final) del día y está lloviendo toma un paraguas, si lo hay para ir de su casa a la oficina y viceversa. Asuma que independiente del pasado llueve al comienzo (final) del día con probabilidad p (0<p<1). Se desea modelar el número de paraguas en su casa al inicio del día n, suponiendo que inicialmente ambos paraguas están en su casa.
El problema sugiere como variable aleatoria el modelamiento del número de paraguas que tiene el individuo en su casa al inicio del día n:
Los posibles estados o valores que puede adoptar la variable aleatoria en una etapa n cualquiera son 0, 1 o 2. Es decir, el individuo podrá tener en su casa al inicio de un día en particular 0, 1 o 2 paraguas.
A continuación corresponde identificar las probabilidades de transición en una etapa, lo cual depende de la dinámica de la situación planteada:
Por ejemplo P(0,0) representa la probabilidad de que un día el individuo no tenga paraguas en su casa (por tanto los 2 paraguas están en la oficina) y que al inicio del día siguiente siga en la misma situación (es decir, sin paraguas en la casa). Los escenarios que permiten esta situación son que llueva en la mañana (con probabilidad p) y que no llueva en la tarde (con probabilidad 1-p). Adicionalmente si no llueve en la mañana (con probabilidad 1-p) y no llueve en la tarde (con probabilidad 1-p) el individuo al inicio del día siguiente no tendrá paraguas en la casa. En consecuencia se puede notar que para este caso lo relevante es que no llueva en la tarde (sin importar si llueve o no en la mañana) para que de esta forma el individuo no se lleve un paragua desde la oficina a la casa.
Otra combinación interesante es P(2,2) que considera la probabilidad de tener los 2 paraguas en la casa al inicio de un día (y por tanto ninguno en la oficina) y al inicio del día siguiente también tener 2 paraguas en la casa. Para ello se debe cumplir alguno de los siguientes escenarios: que llueva en la mañana y en la tarde, que no llueva ni en la mañana ni en la tarde o que no llueva en la mañana pero si llueva en la tarde.
Una vez identificadas todas las probabilidades de transición en una etapa entre estados, éstas se pueden resumen en la matriz de probabilidades de transición (conocida también como matriz P). Notar que la suma de las probabilidades de cada una de las filas de la matriz es (y debe ser) un 100%.
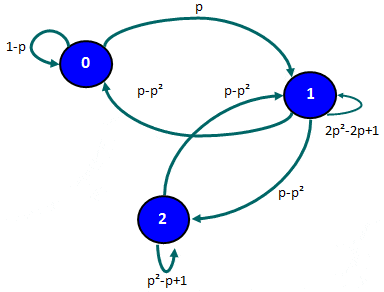
Alternativamente la información anterior se puede representar a través de un grafo donde cada nodo representa un estado y las flechas muestran si es posible pasar de un estado a otro al cabo de una etapa (y cuál es la probabilidad asociada en dicho caso):
Adicionalmente se puede identificar (si se cuenta con dicha información) la distribución inicial de estados que permite identificar cuál es la probabilidad que al inicio de la planificación el proceso se encuentre en alguno de los n estados posibles. En este ejemplo sabemos que se comienza con 2 paraguas en la casa:
Con la información recabada en este problema estamos en condiciones de poder estimar cuál es la probabilidad que comenzando en un estado i pasemos a un estado j al cabo de n etapas (pasos). Este tipo de análisis y otros complementarios los abordaremos en un próximo artículo.
Actualización: Se recomienda consultar el artículo Cadenas de Markov (Ejercicios Resueltos) para encontrar material de estudio complementario al presentado en esta publicación.