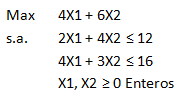El método de Branch and Bound (o Ramificación y Acotamiento) es un algoritmo diseñado para la resolución de modelos de Programación Entera. Su operatoria consiste en linealizar el modelo de Programación Entera, es decir, resolver éste como si fuese un modelo de Programación Lineal y luego generar cotas en caso que al menos una variable de decisión (entera) adopte un valor fraccionario.
El algoritmo genera en forma recursiva cotas (o restricciones adicionales) que favorecen la obtención de valores enteros para las variables de decisión. En este contexto resolver el modelo lineal asociado a un modelo de Programación Entera se conoce frecuentemente como resolver la relajación continua del modelo entero.
Ejemplo Branch & Bound (Ramificación y Acotamiento)
Consideremos el siguiente modelo de Programación Entera el cual resolveremos con el algoritmo de Branch and Bound:
El paso inicial consiste en resolver este problema como si fuese un modelo de Programación Lineal (relajación continua). Si la solución de dicho problema llegara a respetar las condiciones de integralidad para las variables de decisión, ésta ya sería la solución óptima del problema entero.
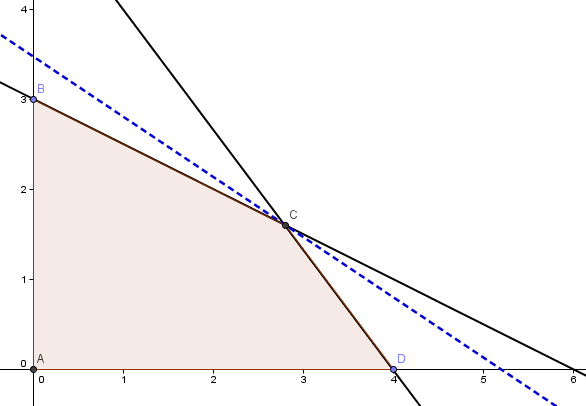
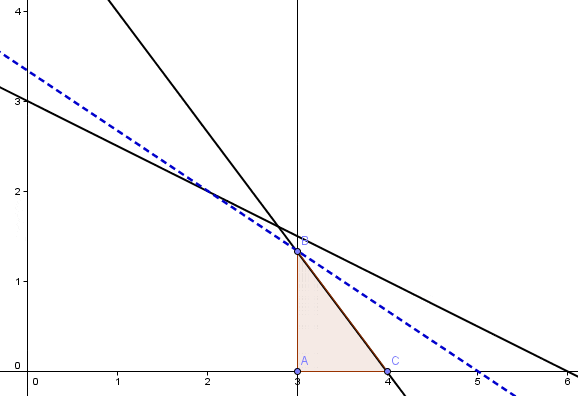
Si bien este procedimiento se puede extender a problemas de mayor dimensión, utilizamos un modelo en 2 variables para poder representar los pasos del algoritmo gráficamente. El gráfico a continuación muestra dicha resolución:
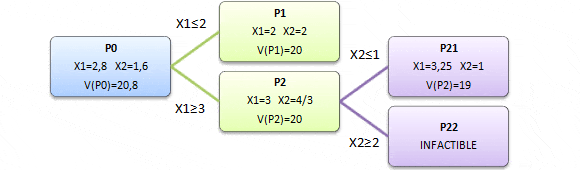
La solución óptima del problema lineal asociado (que llamaremos P0) es X1=2,8 y X2=1,6 con valor óptimo V(P0)=20,8. Claramente esta solución no cumple las condiciones de integralidad para las variables de decisión por tanto es necesario generar cotas o restricciones adicionales de modo de poder obtener soluciones enteras. Para ello debemos seleccionar una de las 2 variables de decisión con valores fraccionarios para poder generar cotas. En estricto rigor es indistinto cuál de ellas seleccionemos debido a que el método nos debe llevar a conclusiones similares (aun cuando la cantidad de pasos requeridos o rapidez de convergencia cambie).
En nuestro ejemplo generaremos cotas adicionales para la variable X1 aproximando su valor actual al entero inferior más cercano (P1) y entero superior más cercano (P2).
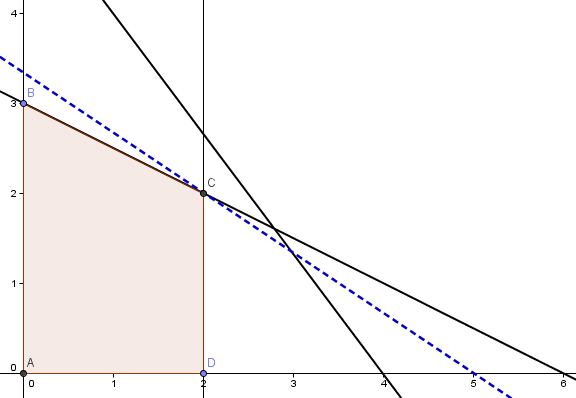
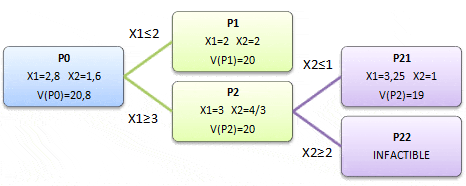
La resolución gráfica del problema 1 (P1) nos da como solución óptima X1=2 y X2=2 que es una solución entera. El valor óptimo del problema 1 es V(P1)=20. Notar que V(P1)<V(P0) lo cual es natural dado que el dominio de soluciones factibles del P1 es menor (subconjunto) al dominio de soluciones factibles de P0.
Análogamente la resolución gráfica (Método Gráfico) del problema 2 (P2) determina que X1=3 y X2=4/3 con V(P2)=20 según se observa a continuación:
Luego no sería del todo necesario seguir desarrollando el algoritmo dado que si generamos cotas para la variable X2 del P2 en ningún caso podríamos obtener una solución entera con valor óptimo superior a 20 (valor que reporta en la función objetivo la actual solución entera de P1) y por tanto podríamos concluir que X1=2 y X2=2 es la solución óptima del problema entero. No obstante el siguiente diagrama muestra los pasos adicionales en caso que quisiera agregar cotas adicionales a partir del P2.
Un argumento similar al expuesto previamente en este caso explicaría la no necesidad de seguir ramificando el P21. Se propone al lector verificar que se obtiene la misma solución óptima si luego del P0 ramificamos a través de X2 agregando las restricciones X2<=1 y X2>=2.