Uno de los teoremas principales en la Teoría de Dualidad en Programación Lineal es el Teorema de Holguras Complementarias.
El Teorema de Holguras Complementarias nos permite encontrar la solución óptima del Problema Dual cuando conocemos la solución óptima del Problema Primal (y viceversa) a través de la resolución de un sistema de ecuaciones conformado por las variables de decisión (primales y duales) y las restricciones (del modelo primal y dual).
La importancia de este teorema radica en que facilita la resolución de los modelos de optimización lineal, permitiendo a quién los resuelve buscar el modelo más sencillo para abordar (desde el punto de vista algorítmico) dado que de cualquier forma podrá obtener los resultados del modelo equivalente asociado (sea éste el modelo primal o dual).
Ejemplo Teorema de Holguras Complementarias
Consideremos el siguiente modelo de Programación Lineal (en adelante Primal) en 2 variables cuya solución óptima obtenida por el Método Gráfico es X=14/5 e Y=8/5 con valor óptimo V(P)=20,8.
El modelo Dual asociado al modelo primal es: (ante dudas de cómo pasar del problema primal al problema dual se recomienda revisar el artículo Relaciones de Dualidad en Programación Lineal (Cómo pasar de Primal a Dual))
Luego, el Teorema de Holguras Complementarias plantea las siguientes relaciones:
Como sabemos X=14/5 e Y=8/5 (Solución Básica Factible Óptima del modelo primal). Si reemplazamos estos valores de X e Y en la tercera y cuarta ecuación generamos un sistema de ecuaciones de 2×2 en términos de A y B cuya solución corresponde a A=6/5 y B=2/5 (solución óptima del modelo dual). Si posteriormente evaluamos en la función objetivo del problema dual dicha solución obtenemos: V(D)=12(6/5)+16(2/5)=20,8 que es similar al valor óptimo del problema primal (Teorema de Dualidad Fuerte).
Siendo A=6/5 y B=2/5 una solución factible para el problema dual, ésta es la solución optima de dicho problema.
Observaciones: Notar que la restricción 1 y 2 del problema primal son activas en el óptimo, es decir, se cumplen en igualdad. Esto permite descartar que A y B (variables duales asociadas a dichas restricciones) son iguales a cero. Si por ejemplo, la restricción 1 del modelo primal no fuese activa en el óptimo se podría afirmar que A es igual a cero en el dual.
Ejercicio Teorema de Holguras Complementarias en Programación Lineal
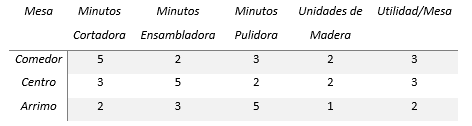
Una empresa que fabrica muebles desea estudiar la producción de varios tipos de mesas de madera. Las mesas a fabricar son mesas de comedor, de centro y de arrimo, las que deben ser procesadas por 3 tipos de máquinas, una cortadora, una ensambladora y una pulidora. Se dispone de a lo mas de 80 horas de trabajo en cada una de las máquinas y 2.000 unidades de madera. La siguiente tabla muestra los tiempos y la madera necesaria para la fabricación de cada mesa, así como la utilidad que reporta cada una de ellas.
Dadas las siguientes soluciones del Problema Primal S1=(900,100,0), S2=(176,496,656), S3=(200,400,550) y S4=(800,0,400). Determine mediante el Teorema de Holguras Complementarias si alguna de estas soluciones es óptima para el Problema Primal planteado.
Sea el Problema Primal el siguiente:
Variables de Decisión:
- X1 : Cantidad de mesas de comedor a producir
- X2 : Cantidad de mesas de centro a producir
- X3 : Cantidad de mesas de arrimo a producir
Función Objetivo:
MAX Z = 3 X1 + 3 X2 + 2 X3
Restricciones:
- 5 X1 + 3 X2 + 2 X3 <= 4.800 (tiempo cortadora)
- 2 X1 + 5 X2 + 3 X3 <= 4.800 (tiempo ensambladora)
- 3 X1 + 2 X2 + 5 X3 <= 4.800 (tiempo pulidora)
- 2 X1 + 2 X2 + 1 X3 <= 2.000 (disponibilidad de madera)
- X1>=0, X2>=0, X3>=0
Su correspondiente Problema Dual asociado es:
MIN W = 4.800 Y1 + 4.800 Y2 + 4.800 Y3 + 2.000 Y4
S.A.
- 5 Y1 + 2 Y2 + 3 Y3 + 2 Y4 >= 3
- 3 Y1 + 5 Y2 + 2 Y3 + 2 Y4 >= 3
- 2 Y1 + 3 Y2 + 5 Y3 + 1 Y4 >= 2
- Y1>= 0, Y2>=0, Y3>=0, Y4>=0
A continuación verificamos la factibilidad de las soluciones propuestas para el Problema Primal:
S1=(900,100,0), V(S1)=3.000 Satisface todas las restricciones
S2=(176,496,656) V(S2)=3.328 Satisface todas las restricciones
S3=(200,400,550) V(S3)=2.900 Satisface todas las restricciones
S4=(800,0,400) V(S4)=3.200 Satisface todas las restricciones
Todas las soluciones satisfacen todas las restricciones por lo que son todas soluciones factibles. De ellas se escoge S2 ya que entrega la mayor utilidad para verificar si es solución óptima: X1=176, X2=496, X3=656.
En restricción (1) holgura X4 = 1.120
En restricción (2) holgura X5 = 0
En restricción (3) holgura X6 = 0
En restricción (4) holgura X7 = 0
De esta forma el Teorema de Holguras Complementarias permite obtener lo siguiente:
Que al ser reducido permite obtener un sistema de ecuaciones de 3×3:
- 2 Y2 + 3 Y3 + 2 Y4 = 3
- 5 Y2 + 2 Y3 + 2 Y4 = 3
- 3 Y2 + 5 Y3 + 1 Y4 = 2
Solución Problema Dual : Y1=0, Y2=1/25, Y3=3/25, Y4=32/25. Al evaluar la solución alcanzada en la función objetivo del dual se obtiene: W=4.800*0+4.800*1/25+4.800*3/25+2.000*32/25=3.328. Por el Teorema de Dualidad Fuerte W=Z por lo tanto S2 es solución óptima del Problema Dual.
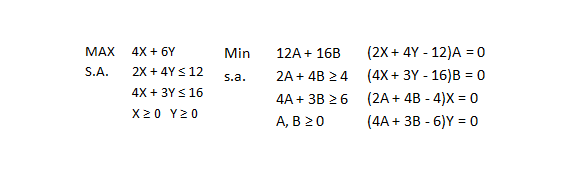
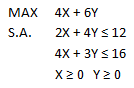
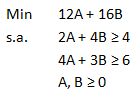
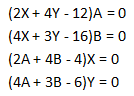
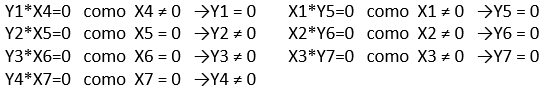
¿Qué pasa si no tenemos las soluciones óptimas en el primal, por qué el problema no esta acotado?
@Moises. Según los resultados de dualidad si el problema primal es infactible, es decir, el dominio de soluciones factibles de dicho problema es vacío, entonces el problema dual asociado es no acotado y sin solución óptima. En este sentido se debe tener en cuenta que un problema con dominio de soluciones factibles no acotado puede (o no) tener solución óptima y esto dependerá de la naturaleza de la función objetivo.