El método de multiplicadores de Lagrange (el cual es generalizado por las condiciones de optimalidad de Karush-Kuhn-Tucker) permite abordar la resolución de modelos de programación no lineal que consideran restricciones de igualdad. En este sentido y como resulta natural, el dominio de soluciones factibles considerará exclusivamente aquellas soluciones que permiten verificar el cumplimiento de la igualdad de dichas restricciones. Por el contrario, un problema de optimización que considera inecuaciones como restricciones, sólo requiere que éstas se cumplan y no necesariamente se deberá forzar el cumplimiento de ellas en igualdad (activas).
En general las condiciones de Lagrange se aplican a un problema que tiene la siguiente estructura:
Que da origen a la función Lagrangiana asociada a dicho problema:
Consideremos el siguiente problema de Programación No Lineal restringido que nos permitirá ilustrar la aplicación del método de Lagrange.
Notar que el problema adopta la estructura estándar previamente descrita y considera una única restricción de igualdad. No se incluye en particular condiciones de no negatividad, que en caso de estar presentes justificarían la aplicación del Teorema de Karush-Kuhn-Tucker.
En este contexto, un mínimo local para el problema propuesto debe satisfacer las condiciones necesarias de primer orden de Lagrange:
Que da origen al siguiente sistema de ecuaciones:
Donde la resolución es trivial y corresponde a x1=2, x2=2 y λ1=-4. Notar que el multiplicador de Lagrange asociado a una restricción de igualdad es libre de signo, en consecuencia la solución propuesta satisface las condiciones necesarias de primer orden.
Adicionalmente se cumplen las condiciones de segundo orden pues:
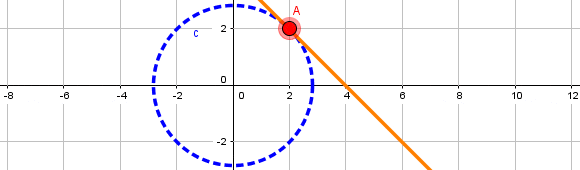
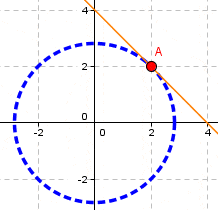
Es positiva definida (función objetivo estrictamente convexa y restricción lineal que define un conjunto convexo). Luego, el problema es convexo y en consecuencia x1=2 y x2=2 es mínimo global y solución óptima del problema. Este resultado por cierto es consistente con la representación gráfica del problema, donde la solución óptima corresponde al punto A, donde la restricción (color naranjo) es tangente a la curva de nivel que representa a la circunferencia de menor radio que intercepta el dominio de soluciones factibles.
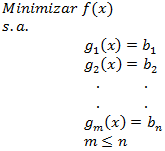
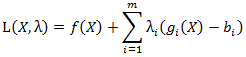
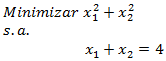
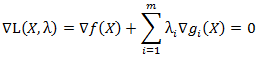
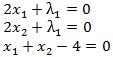
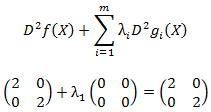
Me ha sido de mucha ayuda esta página, explica muy bien y siempre a vínculos para llegar a los temas relacionados. Gracias!