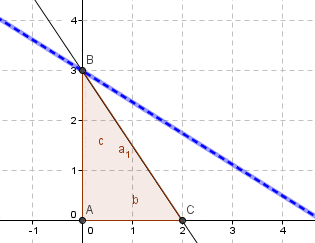
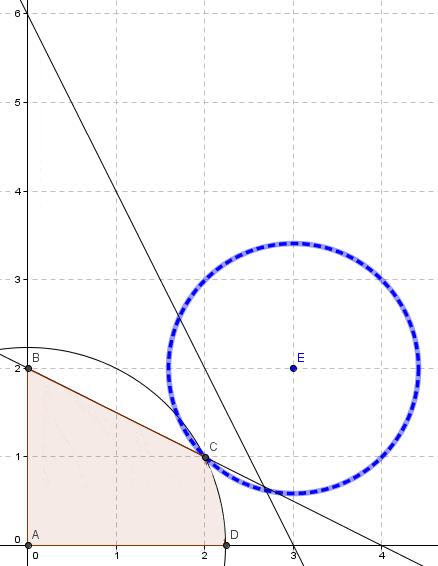
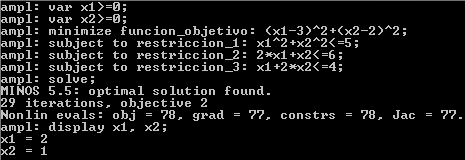
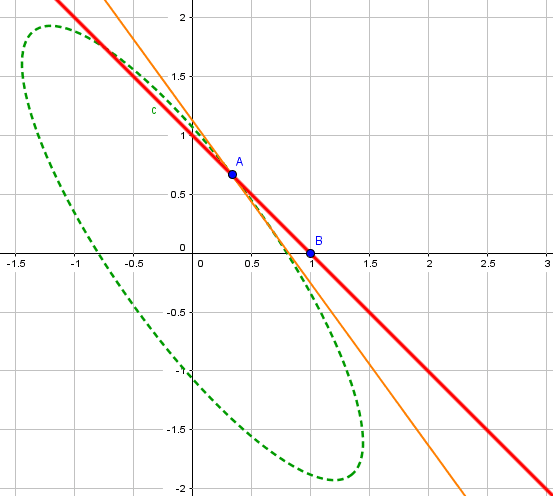
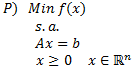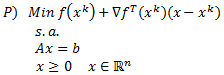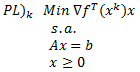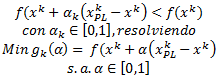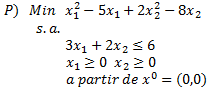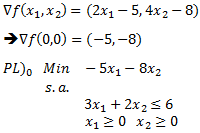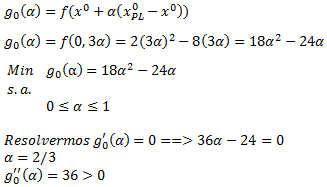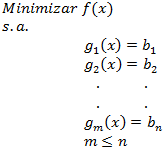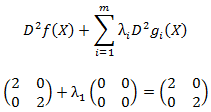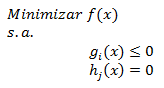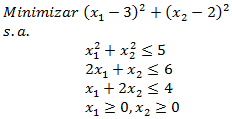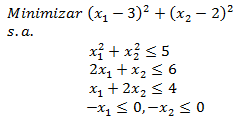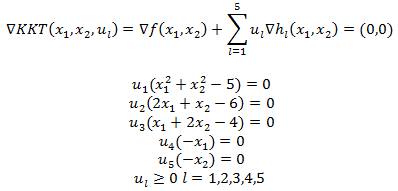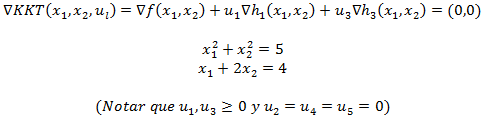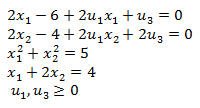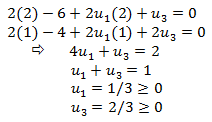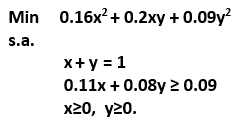Programación No Lineal Archivos - Gestión de Operaciones

Qué es la Programación Estocástica

La Programación Estocástica reúne aquellos modelos de optimización en donde uno o más parámetros del problema son modelados a través de variables aleatorias. Una manera de enfrentar esta aleatoriedad consiste en reemplazar los parámetros aleatorios por su valor esperado, lo cual lleva a resolver un problema determinístico de programación matemática, los cuales son de especial interés en cursos introductorios de Investigación de Operaciones y donde la variabilidad inherente a los parámetros se aborda a través del Análisis de Sensibilidad o Postoptimal.

No obstante, la solución obtenida de esta manera puede no ser representativa de la realidad, al no considerar la dispersión de los valores que toman los parámetros en torno al valor esperado, lo cual entre otras cosas puede invalidar su implementación al resultar finalmente escenarios muy diferentes del promedio.

De este modo y en general, una forma de incorporar esta situación de incertidumbre es considerar un número finito de posibles realizaciones o escenarios para los parámetros aleatorios.

El impacto de la incorporación explicita de la incertidumbre en modelos de programación matemática afecta la factibilidad y optimalidad del sistema en estudio. En efecto, la solución que entrega la resolución de un modelo determinista que considera reemplazar los parámetros aleatorios por su valor esperado, puede ser infactible para un escenario en particular.

En este contexto la connotación que tiene el término factibilidad en programación estocástica es más extensa que en el caso determinista, debido a que no se puede garantizar que la solución del modelo estocástico sea factible para todas las posibles realizaciones de la variable aleatoria. Frecuentemente se incluye términos de penalización en la función objetivos que castigan estas posibles infactibilidades ponderada por un cierto costo según se constata por ejemplo en las investigaciones de Sen, S. and Higle, J.L. (1999). Introductory Tutorial on Stochastic Linear Programming Models. Interfaces 29, No.2, 33-61.

En cuanto al impacto que tiene la incertidumbre sobre la optimalidad del modelo formulado se puede observar que a mayor variabilidad de los parámetros aleatorios, el valor que alcanza la función objetivo varía en torno a una media en mayor magnitud. En este sentido la literatura reúne una serie de indicadores que cuantifica este impacto (Birge, J and Louveaux, F (1997). Introduction to Stochastic Programming, Springer – Verlag, New York, USA) de la incorporación explícita de la incertidumbre en la formulación del modelo y permite al tomador de decisiones dilucidar el real impacto de ésta.

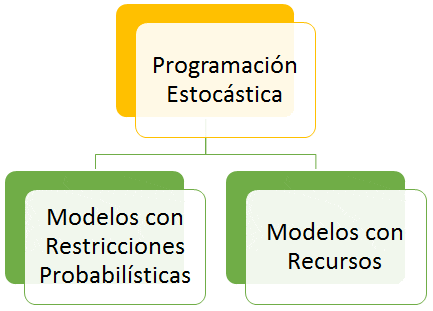
Clasificación de los modelos de Programación Estocástica

Los modelos de optimización estocástica se dividen en dos grandes categorías, estos son: Modelos con Restricciones Probabilísticas y Modelos con Recurso. Una referencia general al respecto lo constituye un tutorial desarrollado por Sen y Higle (1999) sobre programación estocástica para el caso lineal y libros como el de Birge y Louveaux (1997).

Modelos con Recursos en 2 Etapas

En un modelo con recurso en dos etapas se pueden distinguir aquellas variables de decisión que son implementadas antes de la realización particular del parámetro aleatorio denominadas de primera etapa o here and now, que se debe tomar antes de conocer la realización de la variable aleatoria, es decir que se escoge tomando en cuenta la aleatoriedad de los parámetros, pero cuyo valor es independiente de la realización particular que finalmente vaya a tomar dicha variable aleatoria. Las variables de primera etapa pueden ser vistas como decisiones proactivas y están asociadas frecuentemente a decisiones estratégicas como la planificación y expansión de sistemas de producción.

En tanto las variables que son determinadas una vez conocida la realización particular de la variable aleatoria son llamadas de segunda etapa o de recurso, es decir, su valor es tomado en respuesta al medio. En este sentido las variables de segunda etapa son de naturaleza reactiva y generalmente están asociadas a decisiones operativas.

Ejemplo del Método de Frank Wolfe en Programación No Lineal

El método o algoritmo de Frank Wolfe fue propuesto en 1956 por Marguerite Frank y Philip Wolfe y se aplica a problemas de optimización matemática con una función objetivo no lineal convexa y cuyo dominio de soluciones factibles esta compuesto exclusivamente por restricciones lineales, es decir, es un conjunto convexo (en consecuencia el problema es convexo).

Consideremos el siguiente problema que asumiremos cumple con el formato anteriormente descrito:

Dada una aproximación $x^{k}$ a la solución óptima del problema, podemos resolver un problema más sencillo que aproxime al problema P), suponiendo $x^{k}$ factible.

O equivalentemente resolviendo el siguiente problema:

Que puede ser resuelto mediante el Método Simplex. Denotamos por $x_{PL}^{k}$ la solución óptima de $PL_{k}$ . El método contempla en seguida una minimización de un problema unidimensional que equivale a escoger un escalar $\alpha _{k}$ de modo que:

En seguida se define la siguiente aproximación al óptimo como:

Que equivale a definir $x^{k+1}$ como la solución óptima de f restringida al conjunto de puntos que determina al segmento que une $x^{k}$ con $x_{PL}^{k}$ .

Ejemplo: Aplicar el método de Frank Wolfe al siguiente problema no lineal restringido (convexo). Notar que la matriz hessiana o de segundas derivadas de la función objetivo es positiva definida.

Realizamos la primera iteración del método que da origen al siguiente problema de Programación Lineal:

La resolución es trivial y puede ser alcanzada de forma gráfica con Geogebra. La solución óptima es $x_{PL}^{0}=(0,3)$ según se aprecia a continuación:

Luego buscamos la solución para el problema unidimensional en términos del parámetro $\alpha$ :

Finalmente se obtiene $x^{1}=x^{0}+\frac{2}{3}(x_{PL}^{0}-x^{0})=(0,2)$ concluyendo una iteración del método de Frank Wolfe. Se propone al lector seguir las iteraciones a contar de este punto. Por ejemplo se puede verificar que $x_{PL}^{1}=(2,0)$ . (Hint: La solución óptima se alcanza en $(x_{1},x_{2})=(1,\frac{3}{2})$ .

Método del Centroide aplicado a un Problema de Localización de Instalaciones

El Método del Centroide es una técnica para ubicar instalaciones que considera las instalaciones existentes, las distancias entre ellas y la cantidad de productos a transportar entre las mismas. Se suele suponer que los costos de envío o transporte de entrada y salida son iguales y no incluye costos de envío especiales.

La aplicación del Método del Centroide requiere ubicar las instalaciones existentes en un sistema de coordenadas. La elección de dicho sistema de coordenadas es completamente arbitraria, no obstante, actualmente son populares las medidas de longitud y latitud debido a la rápida adopción de los sistemas GPS. Sin perjuicio de lo anterior y con el objetivo de representar ejemplos sencillos se pueden utilizar coordinadas arbitrarias (X,Y).

El Centroide se encuentra calculando las coordenadas X e Y que dan como resultado el costo de transporte mínimo. Para ello se utilizan las fórmulas:

Donde:

Ejemplo Método del Centroide

Se desea determinar la ubicación óptima de una planta productiva (en adelante Planta E) mediante el Método del Centroide con respecto a otras 3 plantas demandantes a las cuales abastece de un cierto producto, que en lo sucesivo denotaremos por A, B y C y cuyas coordenadas (X,Y) son (150,75), (100,300) y (275,380), respectivamente. En este contexto, las plantas A, B y C requieren 6.000, 8.200 y 7.000 unidades anuales, respectivamente, las cuales serán transportadas desde la Planta E. Se supone una relación lineal entre los volúmenes enviados y los costos de envío (sin cargos adicionales).

Dada la información anterior calculamos las coordenadas en X e Y de la Planta E.

¿Minimizará la localización propuesta para la Planta E por el Método del Centroide la sumatoria de la distancia euclidiana respecto a las plantas demandantes A, B y C?. Para responder esta pregunta formulamos el siguiente modelo de Programación No Lineal no restringida:

Luego de implementar el problema anterior en Solver de Excel obtenemos la coordenada (X,Y)=(175,00, 251,67) que determina una sumatoria de distancias totales de 66.266,67[u] que es levemente inferior a la obtenida a través del Método del Centroide donde la sumatoria de las distancias alcanza las 66.662,80[u].

Esta diferencia menor se explica por la relativa similitud de los resultados obtenidos a través de los 2 métodos según se aprecia en la siguiente representación gráfica:

Método de Lagrange aplicado a un Problema de Programación No Lineal

El método de multiplicadores de Lagrange (el cual es generalizado por las condiciones de optimalidad de Karush-Kuhn-Tucker) permite abordar la resolución de modelos de programación no lineal que consideran restricciones de igualdad. En este sentido y como resulta natural, el dominio de soluciones factibles considerará exclusivamente aquellas soluciones que permiten verificar el cumplimiento de la igualdad de dichas restricciones. Por el contrario, un problema de optimización que considera inecuaciones como restricciones, sólo requiere que éstas se cumplan y no necesariamente se deberá forzar el cumplimiento de ellas en igualdad (activas).

En general las condiciones de Lagrange se aplican a un problema que tiene la siguiente estructura:

Que da origen a la función Lagrangiana asociada a dicho problema:

Consideremos el siguiente problema de Programación No Lineal restringido que nos permitirá ilustrar la aplicación del método de Lagrange.

Notar que el problema adopta la estructura estándar previamente descrita y considera una única restricción de igualdad. No se incluye en particular condiciones de no negatividad, que en caso de estar presentes justificarían la aplicación del Teorema de Karush-Kuhn-Tucker.

En este contexto, un mínimo local para el problema propuesto debe satisfacer las condiciones necesarias de primer orden de Lagrange:

Que da origen al siguiente sistema de ecuaciones:

Donde la resolución es trivial y corresponde a x1=2, x2=2 y λ1=-4. Notar que el multiplicador de Lagrange asociado a una restricción de igualdad es libre de signo, en consecuencia la solución propuesta satisface las condiciones necesarias de primer orden.

Adicionalmente se cumplen las condiciones de segundo orden pues:

Es positiva definida (función objetivo estrictamente convexa y restricción lineal que define un conjunto convexo). Luego, el problema es convexo y en consecuencia x1=2 y x2=2 es mínimo global y solución óptima del problema. Este resultado por cierto es consistente con la representación gráfica del problema, donde la solución óptima corresponde al punto A, donde la restricción (color naranjo) es tangente a la curva de nivel que representa a la circunferencia de menor radio que intercepta el dominio de soluciones factibles.

Teorema de Karush Kuhn Tucker en PNL (Ejercicios Resueltos)

Las condiciones de optimalidad establecidas en el Teorema de Karush Kuhn Tucker (KKT) permiten abordar la resolución de modelos de Programación No Lineal que consideran tanto restricciones de igualdad (ecuaciones) como desigualdad (inecuaciones).

En términos comparativos las condiciones de KKT son más generales que el Método de Lagrange el cual se puede aplicar a problemas no lineales que consideran exclusivamente restricciones de igualdad.

En el siguiente artículo mostraremos cómo utilizar el Teorema de Karush Kuhn Tucker para resolver un problema de Programación No Lineal con 2 variables de decisión.

Sin pérdida de generalidad un modelo de Programación No Lineal se puede representar a través del siguiente formato:

Luego podemos reescribir cualquier problema en dicha estructura manteniendo la equivalencia de la representación matemática. Para ejemplificar lo anterior consideremos el siguiente modelo de optimización no lineal que resulta de interés su resolución.

El problema anterior se puede representar gráficamente a través del software Geogebra de modo de encontrar su solución óptima (x1=2 y x2=1) en el par ordenado etiquetado con la letra «C» en el gráfico a continuación, con valor óptimo V(P)=2.

El conjunto de factibilidad corresponde al área achurada. Adicionalmente se puede observar que en la solución óptima se encuentran activas las restricciones 1 y 3 (el resto de las restricciones por cierto se cumple pero no en igualdad).

Por supuesto la resolución mediante el Método Gráfico es sólo referencial y se ha utilizado en este caso para corroborar los resultados a obtener en la aplicación del teorema. En este contexto el problema en su forma estándar es simplemente:

Notar que sólo fue necesario cambiar la forma de las restricciones de no negatividad (esto se puede hacer multiplicando por -1 cada una de ellas). Cabe destacar que en este caso en particular el problema no considera restricciones de igualdad.

Luego las condiciones necesarias de primer orden de Karush Kuhn Tucker (KKT) están dadas por:

Por ejemplo, si en las condiciones generales anteriores consideramos el problema no restringido (asumiendo que todas las restricciones son inactivas) la solución óptima por simple inspección es x1=3 y x2=2, que corresponde a la coordenada «E» de la gráfica anterior y que se puede observar no es una solución factible para el problema.

De este modo la circunferencia de menor radio que intercepta el conjunto de factibilidad es precisamente aquella que pasa por la coordenada «C» donde las restricciones 1 y 3 se cumplen en igualdad, razón por la cual las cuales activaremos de forma simultanea:

Al calcular los gradientes respectivos se obtiene:

Lo cual da origen al siguiente sistema de ecuaciones:

Reemplazando x1=2 y x2=1 podemos despejar los valores de los multiplicadores los cuales cumplen con las condiciones de no negatividad:

Adicionalmente se puede verificar que x1=2 y x2=1 satisface las restricciones omitidas (2, 4 y 5) por lo cual se puede afirmar que dicha solución cumple las condiciones necesarias de primer orden de Karush Kuhn Tucker (KKT).

A continuación verificamos el cumplimiento de las condiciones de segundo orden de KKT, en particular lo que tiene relación con la convexidad del problema. Para ello calculamos la Matriz Hessiana o de segundas derivadas de la función objetivo y las restricciones activas.

El primer determinante de la Matriz Hessiana es D1=8/3>=0 y el segundo determinante es D2=(8/3)*(8/3)=(64/9)>=0. Se concluye que el problema es convexo y por tanto x1=2 y x2=1 es mínimo local y global para el problema. La resolución computacional de este problema con AMPL corrobora los resultados alcanzados:

Ejercicio Resuelto Teorema de Karush Kuhn Tucker (KKT)

Un asesor financiero está evaluando la compra de acciones de firmas de cierto sector industrial. Desea minimizar la variación de la cartera resultante compuesta por acciones de dos firmas, pero también quiere tener un tasa de retorno de al menos un 9%. Después de obtener datos históricos sobre la variación y rendimientos de ambos instrumentos, desarrolla el siguiente modelo de optimización no-lineal:

Donde x e y representan la proporción de dinero invertida en cada acción. Formule explícitamente todas las condiciones de optimalidad del Teorema de Karush-Kuhn-Tucker para este problema y úselas para determinar la cartera óptima. Justifique adecuadamente su respuesta. Analice todos los posibles casos.

Respuesta:

Según el Teorema de Weierstrass, el problema admite solución óptima pues tiene una función objetivo continua y un dominio de soluciones factibles cerrado y acotado (que se puede apreciar incluso geométricamente). En este sentido el dominio de soluciones factibles son los puntos en la recta que unen los pares ordenados etiquetados con las letras A y B, donde:

$A=(x,y)=(\frac{1}{3},\frac{2}{3})$ y $B=(x,y)=(1,0)$

Más aún es fácil ver que la Matriz Hessiana de la función objetivo es positiva definida y por ende es una función (estrictamente) convexa.

$\bigtriangledown f(x,y)=(0.32x+0.20y,0.20x+0.18y)$

$H=D^{2}(x,y)=\begin{pmatrix}0.32&0.20\\0.20&0.18\end{pmatrix}$

Como las restricciones son lineales, y la función objetivo es estrictamente convexa, resulta que es problema propuesto es un problema convexo.

Lo anterior (que el problema sea convexo) implica que las condiciones de optimalidad de Karush-Kuhn-Tucker son necesarias y suficientes para hallar la solución óptima del mismo.

Las condiciones del Teorema de Karush-Kuhn-Tucker para este problema son:

i)
0.32x + 0.20y + λ1 – 0.11μ1 – μ2 = 0
0.18y + 0.20x + λ1 – 0.08μ1 – μ3 = 0
ii)
(-0.11x – 0.08y + 0.09) μ1 = 0
-x1 μ2 = 0 -x3 μ3 = 0
iii)
x + y = 1
0.11x + 0.08y ≥ 0.09
x≥0, y≥0
iv)
μ1≥0, μ2≥0, μ3≥0

Al considerar el esquema de activación de restricciones, siempre debe estar activa la ecuación x+y =1 y lo que cabe entonces es no activar ninguna inecuación o a lo sumo activar una de ellas.

Los diferentes casos que se podrían llegar a analizar son:

i) Ninguna inecuación activa.

Tomamos μ1=0, μ2=0, μ3=0 y resolvemos:

0.32x + 0.20y + λ1 = 0
0.18y + 0.20x + λ1 = 0
x + y = 1

Cuya solución resulta ser: x=-0.2 e y=1.2 que es infactible.

ii) Activando sólo la inecuación 0.11x + 0.08y ≥ 0.09.

Tomamos μ2=0, μ3=0 y resolvemos:

0.32x + 0.20y + λ1 – 0.11μ1 = 0
0.18y + 0.20x + λ1 – 0.08μ1 = 0
x + y = 1
0.11x + 0.08y = 0.09

Cuya solución resulta ser: x=1/3 e y=2/3 con multiplicadores λ1=0,04444453 y μ1=1,777777502, con lo cual tenemos un punto que cumple con todas las condiciones del teorema.

iii) Activando sólo la inecuación x≥0.

Tomamos μ1=0, μ3=0 y resolvemos:

0.32x + 0.20y + λ1 – μ2 = 0
0.18y + 0.20x + λ1 = 0
x + y = 1
x = 0

Cuya solución resulta ser: x=0 e y=1 con multiplicadores λ1=-0.18 y μ2 = 0.02 pero no verifica 0.11x + 0.08y = 0.08 ≥ 0.09.

iv) Activando sólo la inecuación y≥0.

Tomamos μ1=0, μ2=0 y resolvemos:

0.32x + 0.20y + λ1 = 0
0.18y + 0.20x + λ1 – μ3 = 0
x + y = 1
y = 0

Cuya solución resulta ser: x=1 e y=0 con multiplicadores λ1=-0.32 y μ3=-0.12 y este último no cumple con la no-negatividad.

En consecuencia, la solución óptima es aquella obtenida en el caso ii) pues el problema es convexo: x=1/3 e y=2/3. Dicha solución corresponde al par ordenado etiquetado con la letra A en la gráfica anterior. El valor óptimo es 0.102222 y se obtiene simplemente al evaluar la solución óptima en la función objetivo.