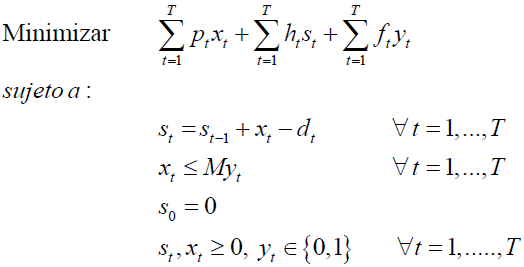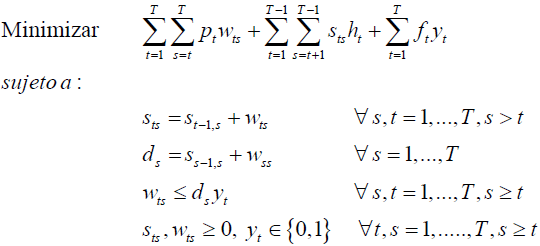costo emisión Archivos - Gestión de Operaciones

Ejemplo del Algoritmo de Wagner y Whitin (Sistemas de Loteo)

El Algoritmo de Wagner y Whitin (1958) consiste en una extensión natural y dinámica al problema de Tamaño Económico de Pedido (conocido también como Cantidad Económica de Pedido o EOQ) donde la demanda durante el período de planificación presenta variabilidad, no obstante, se sigue manteniendo el supuesto de asumir que dicha demanda es conocida.

De esta forma, dada una demanda que presenta variabilidad en el tiempo, costos de emisión de pedidos asociados a la gestión de los mismos y no al volumen involucrado en ellos, y costos de almacenamiento correspondientes al inventario de los productos almacenados en inventario, se busca determinar una política de pedidos que satisfaga los requerimientos de demanda al menor costo posible.

En este contexto asumiremos que el lead time (tiempo de reposición) es nulo, es decir, el pedido se recibe en el mismo período en el que se realiza y que adicionalmente estamos frente a un Problema de Tamaño de Lote No Capacitado, vale decir, que no existe limitantes de capacidad y que, eventualmente, se podría satisfacer la demanda íntegra del horizonte de planificación a través de un único pedido que se realice en el primer período (mediante la acumulación de inventarios para períodos futuros).

Un problema similar al que se aborda con el Algoritmo de Wagner y Whitin es el Problema de Producción e Inventario, en el cual frecuentemente se incorporan limitantes de capacidad para la cantidad de unidades que se pueden pedir en cada período, constituyendo de esta forma un problema capacitado.

Algoritmo de Wagner-Whitin

Los pasos detallados para la implementación del Algoritmo de Wagner y Whitin pueden encontrarse en la publicación académica original: Dynamic Version of the Economic Lot Size Model, (Versión Dinámica del Tamaño Económico de Pedido) disponible para descarga por un valor de 30 dólares. No obstante, a continuación resumiremos los pasos del algoritmo y presentaremos un ejemplo de su aplicación para favorecer su comprensión.

Paso 1: Considere la política de ordenar en el período $t^{**}$ , $t^{**}=1,2,$ …, $t^{*}$ y satisfacer las demandas $d_{t}$ , $t=t^{**},t^{**}+1,$ …, $t^{*}$ en ese orden.
Paso 2: Determine el costo total de las $t^{*}$ políticas de pedido, sumando los costos de emisión y almacenamiento asociados a la emisión de un pedido en $t^{**}$ , y el costo de actuar de forma óptima entre el período 1 y el período $t^{**}-1$ consideradas por si mismas.
Paso 3: De las $t^{*}$ alternativas, seleccione la política de mínimo costo del período 1 hasta $t^{*}$ consideradas de forma independiente.
Paso 4: Continué al período $t^{*}+1$ o detengase si $t^{*}=N$ donde $N$ representa el horizonte de planificación.

Ejemplo del Algoritmo de Wagner y Whitin

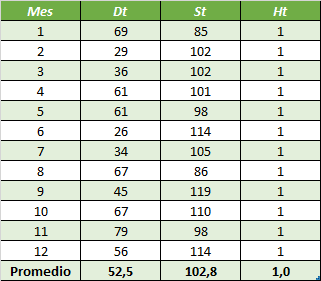
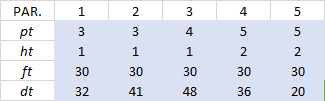
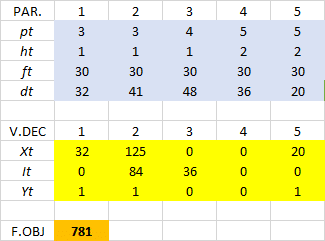
Consideremos las necesidades asociadas a un producto cualquiera para un período de planificación de 12 meses (N=12). La demanda Dt que se enfrenta cada mes es variable, como así también los costos de emitir un pedido (St), no obstante, el costo unitario de almacenar una unidad en inventario de un mes a otro (Ht) por simplicidad se asumirá que es fijo.

Aplicamos a continuación el Algoritmo de Wagner y Whitin:

El plan óptimo para el período 1 es ordenar (asumiendo un costo de emisión de $85).

Para el período 2 se deben evaluar 2 posibilidades:

ordenar en el período 2 y usar la mejor política para el período 1 considerado por si solo (con un costo de emisión de $102+$85=$187).
o emitir un pedido en el período 1 para ambos períodos (1 y 2), almacenando inventario para el período 2 (con un costo total de $85+$29=$114).

En este caso comparativamente es mejor la segunda alterativa.

En el período 3 existen tres alternativas:

emitir un pedido en el período 3 y utilizar la mejor política para los períodos 1 y 2 (a un costo de $102+$114=$216).
o emitir un pedido en el período 2 para los 2 últimos períodos (2 y 3) y utilizar la mejor política para el período 1 considerado de forma independiente (a un costo de $102+$36+$85=$223).
o emitir un pedido en el período 1 para los 3 períodos (con un costo de $85+$29+$36+$36=$186).

En nuestro ejemplo, resulta evidente que no existen incentivos para almacenar productos en inventario en el período 1 o 2 para satisfacer la demanda del período 4, dado que los costos de almacenamiento excederían los costos de emisión de pedido en el período 4. Si lo anterior es cierto, claramente no tiene sentido guardar inventario en el período 1 o 2 para satisfacer demanda de un período superior al 4 (5, 6, 7, etc).

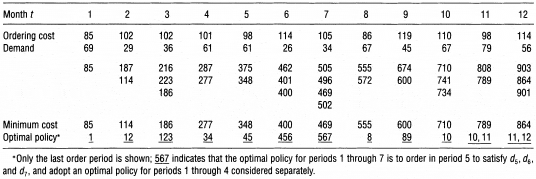
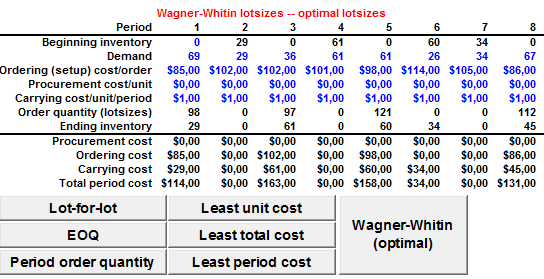
Para los datos propuestos en nuestro ejemplo, la política óptima de pedidos según el Algoritmo de Wagner Whitin es la siguiente:

Pedir 135 unidades (79+56) en el período 11 para satisfacer los requerimientos del período 11 y 12, y utilizar la política óptima para los períodos del 1 al 10.
Emitir un pedido de 67 unidades para el período 10 y utilizar la política óptima de pedidos para los períodos 1 al 9.
Pedir 112 unidades (67+45) en el período 8 para satisfacer la demanda de los períodos 8 y 9, y luego utilizar la mejor alternativa para los períodos del 1 al 7.
Ordenar 121 unidades (61+26+34) en el período 5 para enfrentar la demanda de los períodos 5, 6 y 7.
Pedir 97 unidades (36+61) en el período 3 para satisfacer la demanda de los períodos 3 y 4.
Finalmente pedir 98 unidades (69+29) en el período 1 y con ello cumplir la demanda de los períodos 1 y 2.

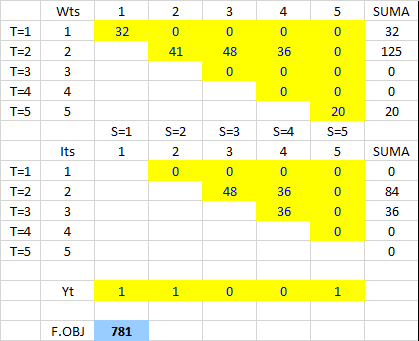
La siguiente tabla resume los resultados anteriormente expuestos.

Al pie del cuadro resumen se detalla, por ejemplo, «567 indica la política óptima de pedido para los períodos del 1 al 7 es pedir en el período 5 y satisfacer la demanda de los períodos 5, 6 y 7 y adoptar una política óptima para los períodos 1 al 4 considerados de forma separada».

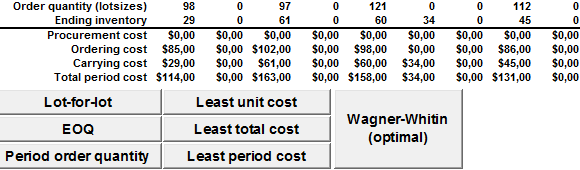
El costo asociado a implementar el Algoritmo de Wagner y Whitin al problema propuesto como ejemplo es de $864. Se propone al lector corroborar que dicha política minimiza los costos de inventario en comparación a otros sistemas de loteo como Costo Total Mínimo, Costo Unitario Mínimo, EOQ, entre otras.

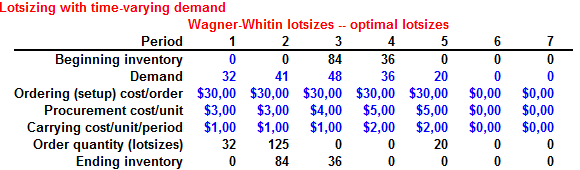
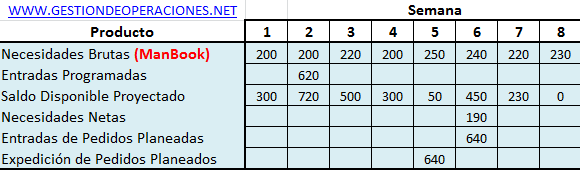
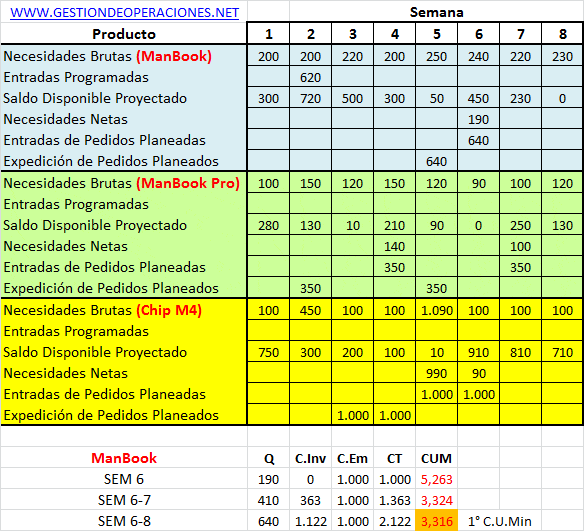
Una forma de corroborar los resultados obtenidos es mediante una aplicación en Excel que permite automatizar los procesos de cálculo. Básicamente ingresando un inventario inicial (en nuestro ejemplo cero), la demanda pronosticada, los costos de emisión de pedidos y los costos de almacenamiento, se puede fácilmente aplicar una política de lotificación como aquellas que tratamos en extenso en el Plan de Requerimientos de Materiales (MRP).

Observación: La imagen anterior ha sido editada para efectos de una mejor resolución de modo que solo se visualiza los resultados parciales hasta el período 8. El archivo Excel con la aplicación donde se encuentran los resultados del ejemplo desarrollado en este artículo, como también la posibilidad de poder utilizarlo con otras políticas de lotificación se puede descargar a continuación.

[sociallocker]Descarga Aquí el Archivo Excel del Algoritmo de Wagner y Whitin: lotsizing[/sociallocker]

Problema de Tamaño de Lote No Capacitado (Formulación y Resolución en Solver)

El Problema de Tamaño de Lote No Capacitado o ULS (por sus siglas en inglés, Uncapacitated Lot-Sizing), consiste en decidir sobre un Plan de Producción para un horizonte de T periodos para un solo producto. El objetivo consiste en minimizar la sumatoria de los costos de producción, almacenamiento de productos en inventario y setup (costos de emisión), asumiendo que las demandas son conocidas en cada uno de los T periodos y éstas deben ser satisfechas de forma íntegra.

Una formulación típica del Problema de Tamaño de Lote No Capacitado considera los siguientes parámetros y variables de decisión.

Formulación Tradicional Problema de Tamaño de Lote No Capacitado

Variables de Decisión:

$x_{t}$ = cantidad producida en el periodo t.
$s_{t}$ = inventario al final del periodo t.
$y_{t}$ = 1 si la producción ocurre en el periodo t, 0 si no.

Parámetros:

$f_{t}$ = costo fijo de producción en el periodo t.
$p_{t}$ = costo unitario de producción en el periodo t.
$h_{t}$ = costo unitario de almacenamiento en el periodo t.
$d_{t}$ = demanda en el periodo t.

La definición anterior da origen al siguiente problema de Programación Entera Mixta (PEM).

La función objetivo consiste en minimizar la suma de los costos de producción, costos de almacenamiento de productos en inventario y costos de emisión de pedidos, para todo el horizonte de planificación (T períodos).

Por otra parte las restricciones del problema quedan definidas por:

Balance de Inventario $s_{t}=s_{t-1}+x_{t}-d_{t}$ : El inventario al final de un período t es igual al inventario al final del período anterior (t-1) más lo producido en el período t y menos lo demandado en el período t.

Capacidad de Producción $x_{t}\leq M\cdot y_{t}$ : Si bien hemos definido el problema como no capacitado, esta restricción permite vincular la decisión de producción en un período con la cantidad (volumen) de dicha producción. De esta forma se evita situaciones anómalas como que en un período cualquiera se produzca y al mismo tiempo el $y_{t}$ respectivo sea cero.

Además, asumiremos que la constante M es lo suficientemente grande (por ejemplo, la suma de las demandas para el horizonte de planificación). En términos prácticos esto hace que el problema no tenga limitantes de capacidad (es decir, es no capacitado) y que, en un extremo, podría producir en el primer período todo lo requerido durante el horizonte de planificación para luego ir satisfaciendo dichos requerimientos con los remanentes de inventario.

Inventario Inicial $s_{0}=0$ : Se asume que no se dispone de inventario al inicio del horizonte de planificación.

Finalmente se establecen condiciones de no negatividad y binarios a las variables según corresponda.

Alternativamente se propone otra formulación como alternativa al Problema de Tamaño de Lote No Capacitado.

Formulación Dinámica Problema de Tamaño de Lote No Capacitado

Variables de Decisión:

$w_{ts}$ = cantidad producida en el periodo t para satisfacer la demanda en el periodo s.
$s_{ts}$ = inventario al final del periodo t destinado para el periodo s.
$y_{t}$ = 1 si la producción ocurre en el periodo t, 0 si no.

Al conservar la definición de parámetros definida para la formulación anterior, se propone el siguiente modelo de Programación Entera:

De modo de corroborar la equivalencia de las formulaciones anteriores se propone una instancia sencilla que corresponde a 5 períodos de planificación (T=5) y donde los valores de los parámetros se resumen en la siguiente tabla. Por ejemplo, $p_{1}=3$ representa el costo de producción unitario en el período 1.

La solución óptima alcanzada con la Formulación Tradicional del Problema de Tamaño de Lote No Capacitado ULS se observa en las celdas de color amarillo en la imagen a continuación. Se producen 32, 125 y 20 unidades en los períodos 1, 2 y 5, respectivamente, almacenando sólo productos en inventario al final del período 2 y 3 (84 y 36 unidades, respectivamente). El valor óptimo (costo total) asciende a $781.

De forma análoga la solución óptima obtenida con la Formulación Dinámica del Problema de Tamaño de Lote No Capacitado ULS se observa en las celdas de color amarillo en la tabla a continuación.

Notar que $w_{11}=32$ , es decir, en el primer período se produce sólo lo necesario para satisfacer los requerimientos de dicho período. Adicionalmente $w_{22}=41$ , $w_{23}=48$ y $w_{24}=36$ , es decir, en el período 2 se producen en total 125 unidades (41+48+36), para satisfacer la demanda de los períodos 2, 3 y 4. Por último en el período 5 se produce simplemente 20 unidades ( $w_{55}=20$ ) para cumplir lo requerido.

Naturalmente dado lo descrito, la solución alcanzada en la Formulación Dinámica del ULS es equivalente a la obtenida en la Formulación Tradicional del ULS.

Se puede consultar otras variantes de Problemas de Planificación de la Producción en nuestro sitio donde se detalla diversas formulaciones e instancias de problemas de esta naturaleza, donde destaca la contribución de la Investigación de Operaciones como herramienta de apoyo para la toma de decisiones.

[sociallocker]Descarga Aquí el Problema de Tamaño de Lote No Capacitado (ULS)[/sociallocker]

Qué es Just in Time (JIT o Justo a Tiempo)

La filosofía de manufactura Just in Time (conocido simplemente por su acrónimo JIT en inglés o en su traducción al español Justo a Tiempo) postula que se debe producir solo lo que sea necesario, en la cantidad que sea necesaria y en el momento que sea necesario. Lo anterior establece como un imperativo de cualquier negocio que aspira ser de Clase Mundial (World Class) la reducción de capital inmovilizado con el correspondiente impacto en la eficiencia de los procesos y la reducción de costos.

Qué hace el Just in Time (JIT)

Just in Time (Justo a Tiempo) se basa sobre 3 pilares u objetivos básicos:

Atacar los problemas fundamentales
Eliminar despilfarros (desperdicios)
Buscar la simplicidad

1. Atacar los Problemas Fundamentales

Consiste en atacar las causas fundamentales de los problemas, resolviendo éstos sin encubrirlos. El enfoque anterior se puede representar a través de una analogía denominada “mar de las existencias” que indica básicamente que el nivel de inventario o existencias suele ocultar problemas en los procesos.

El nivel del mar representa las existencias o inventario y las operaciones de la empresa se visualizan como un barco. Cuando una empresa intenta bajar el nivel del mar, en otras palabras, reducir el nivel del inventario, descubre rocas, es decir, problemas.

El solo hecho de identificar los problemas no garantiza por cierto que estos se resuelvan, sin embargo, se cimientan las bases para poder enfrentar las causas que lo generan (acá se puede hacer uso de metodologías complementarias de la Gestión de Calidad como el Diagrama de Ishikawa y Diagrama de Pareto). De esta forma se deba atacar las causas de los problemas que causan las ineficiencias y no sólo concentrarse en los síntomas o efectos.

En palabras del ingeniero japones Taiichi Ohno, precursor de la filosofía Just in Time (JIT) al interior del sistema de producción del fabricante de automóviles Toyota.

Si se ha entendido bien lo que es el control de la producción, entonces es innecesario el control de inventarios.

De esta forma y en consecuencia a lo discutido anteriormente se pueden establecer diferencias entre el enfoque Tradicional y el enfoque de Just in Time JIT:

2. Eliminar Despilfarros (Desperdicios)

El desperdicio (waste en inglés) se refiere a toda inversión de costo, tiempo, material, mano de obra o recursos aplicada en exceso versus lo mínimo indispensable para ofrecer un Producto y/o Servicio que exceda cualitativa y cuantitativamente las expectativas del cliente.

De esta forma en la manufactura Justo a Tiempo (JIT) el énfasis debe estar en eliminar todas aquellas actividades que no añaden valor al producto con lo que se reduce costos, mejora la calidad, reduce los plazos de fabricación (lead time logístico) y aumenta el nivel de servicio al cliente (que se puede medir cuantitativamente a través de indicadores como Instock, Fill-rate, entre otros).

Algunos ejemplos de los tipos de desperdicios más comunes son:

1. Sobreproducción
2. Tiempo de Espera
3. Transporte
4. Inventario
5. Proceso inadecuado (reprocesamiento)
6. Movimientos innecesarios
7. Defectos en Productos

Luego una forma de poder enfrentar los desperdicios es a través de un enfoque sistémico como el propuesto en JIT que se basa en los siguientes criterios:

Hacer el producto y/o prestar el servicio bien en la primera oportunidad
El operario asume la responsabilidad de controlar, es decir, el operario trabaja en autocontrol
Garantizar el buen desempeño del proceso mediante el Control Estadístico de Procesos (CEP)
Analizar y prevenir los riesgos potenciales que hay en un Proceso
Reducir stocks (Inventarios) al máximo

De esta forma se pueden establecer metas ambiciosas que sean consistentes con el objetivo de eliminar los desperdicios. Entre ellas destacan:

􀂋Cero defectos (Seis Sigma)
􀂋Cero Tiempo de Preparación (Setup Time)
􀂋Cero Inventarios
􀂋Cero Manejo de Materiales
􀂋Cero Lead Time (Plazos)
􀂋Tamaño de Lote Unitario (Q* bajos)
􀂋Productos que satisfagan las necesidades (Calidad)

3. Buscar la Simplicidad

Por regla general los enfoques de producción simples están asociados a una gestión más eficaz. El primer tramo del camino hacia la búsqueda de la simplicidad abarca 2 zonas:

Flujo de Material
Control de las Líneas de Flujo

Un enfoque simple respecto al flujo de material es eliminar las rutas complejas y priorizar líneas de flujo más directas, en lo posible unidireccionales. Otra alternativa es agrupar los productos en familias que se fabrican en una línea de flujo, con lo que se facilita la gestión en células de producción (celdas de manufactura).

De forma complementaria la simplicidad del Justo a Tiempo (JIT) también se aplica al manejo de las líneas de flujo. Un ejemplo de ello es el sistema Kanban, en el que se arrastra el trabajo (sistema Pull o Jalar que consiste en producir sólo lo necesario, tomando el material requerido de la operación anterior).

En resumen el enfoque Just in Time (JIT) o Justo a Tiempo se basa en el control físico del material para identificar los desperdicios y forzar su eliminación. JIT es una filosofía propia de la Ingeniería Industrial que consiste en la reducción de desperdicio (actividades que no agregan valor) es decir todo lo que implique sub-utilización en una Cadena de Suministro desde compras hasta producción.

Requisitos del Just in Time (JIT)

1. 􀂋Nivelado de la Producción: consiste en adaptar los niveles de producción a los cambios que se observan en el comportamiento de la demanda. De esta forma se busca que el Plan Maestro de la Producción sea altamente sensible y adaptable a la aleatoriedad de la Demanda, disminuyendo al mínimo la producción de unidades innecesarias.

2. Estandarización de Operaciones: se busca que los niveles de producción sean equilibrados en todos los procesos utilizando la cantidad mínima de operaciones y recursos, además de minimizar el trabajo en curso (WIP).

3. 􀂋Reducción del Tiempo de Fabricación: consiste en implementar un conjunto de estrategias congruentes que apunten a la reducción de los tiempos requeridos para fabricar los productos. Destaca la reducción del tiempo de operación en cada proceso, reducción de los tiempos de transporte y la reducción de los tiempos de espera o tiempos muertos entre procesos (esto último, por ejemplo, a través del Balance de una Línea de Ensamble).

4. 􀂋Reducción del Tiempo de Preparación: usualmente se asume el setup como irreducible y dado, en efecto en las fórmulas tradicionales de Lote Económico (EOQ) se observa un trade off entre los costos de emisión de pedidos y los costos de almacenamiento de inventario. En este sentido la filosofía JIT reconoce la importancia de reducir el tiempo de emisión o preparación al mínimo posible.

De esta forma bajos setups y lotes pequeños llevan naturalmente a bajos lead times, 􀂋acortando el horizonte de planificación y el pronóstico es mas preciso. Adicionalmente 􀂋el sistema puede cambiar rápido para atender un cambio en la demanda, aumentando la flexibilidad del sistema.

5. Distribución en Planta y Polivalencia: se busca privilegiar a través de la distribución de planta o layout y un esquema de organización del trabajo colaborativo y polivalente, de modo de aprovechar al máximo la disponibilidad de tiempo y capacidades de los trabajadores.

Consistente con esta estrategia se puede utilizar el tiempo sobrante (disponible) para múltiples propósitos con fines productivos entre los que destacan: transferencia de trabajadores a otras líneas, disminución de horas extraordinarias, reuniones de círculos de calidad, prácticas en mejora de programación, mantenimiento y reparación de máquinas, mejora de herramientas e instrumentos, etc.

Cómo implementar Just in Time (JIT) en la Empresa

􀂋La adopción del sistema de manufactura Justo a Tiempo o JIT debe nacer como parte de una Planificación Estratégica, es decir, con una mirada de largo plazo que sea consistente con la 􀂋adaptación de los requisitos y principios del JIT, bajo un ambiente de control y evaluación constante.

En este contexto implementar Just in Time (JIT) no es sencillo y se debe lidear con un importante numero de obstáculos que dificultan su adopción, entre los que destacan:􀂋

Compromiso de la Directiva y Trabajadores
Disciplina de Trabajo
Redistribución de la Planta
Relación con los Proveedores

Por tanto no se deben hacer falsas expectativas esperando resultados a corto plazo.

En relación a aquellas empresas que se enfrentan por primera vez a la implementación de un sistema JIT se recomienda la utilización de un proyecto piloto que cumpla con los siguientes requisitos:

No debe ser un producto nuevo
El proceso debe ser conocido
No se debe escoger un producto crónico o problemático
No se debe escoger un producto con atraso para su entrega

De esta forma se pueden acotar los riesgos asociados a una deficiente implementación.

Finalmente en relación a la metodología de implementación se identifican 5 fases secuenciales que dada la evidencia empírica son adecuadas para la ejecución del JIT:

􀂋Primera Fase: Educación (clave)
􀂋Segunda Fase: Distribución y Polivalencia
􀂋Tercera Fase: Mejoras en el proceso
􀂋Cuarta Fase: Mejoras en el control
Quinta Fase: La ejecución

Just in Time (JIT) o Justo a Tiempo orienta a los procesos para que éstos funciones de forma correcta, correctamente la primera vez.

Ejemplo Resuelto MRP (Plan de Requerimiento de Materiales)

En el siguiente artículo abordamos un ejemplo resuelto MRP (Plan de Requerimiento de Materiales) para 2 productos finales y un insumo con demanda dependiente que permite su fabricación. En el ejemplo se abordan las políticas de lotificación de Costo Unitario Mínimo y Tamaño Fijo de Pedido, explicando con detalle cómo se aplican dichos criterios para determinar el tamaño de los pedidos y el momento en el cual se emiten, de modo de satisfacer las necesidades netas de los productos en consideración.

La empresa Manzana produce y distribuye computadores. Dos de sus modelos más famosos, ManBook y ManBook Pro, usan el mismo chip en su interior (sólo se diferencian por los materiales de sus carcasas), el M4. El problema que ha tenido esta compañía con sus productos estrella, es que el chip en su interior se calienta demasiado y falla. Por esto, se debe considerar una demanda independiente del chip M4 de 100 unidades semanales, las cuales son para venta directa a clientes a través de los servicios técnicos. Los ManBook y ManBook Pro son armados por Manzana en cantidades mínimas de producción, pero el chip M4 es comprado a un proveedor asiático el cual impone un volumen mínimo de compra. La demanda estimada para los ManBook y ManBook Pro para las próximas ocho semanas es:

Además, se sabe que: el tamaño de lote para el ManBook Pro y el chip M4 es igual a la cantidad mínima de producción/compra. Antecedentes adicionales se resume en la siguiente tabla correspondiente al Registro del Inventario o IRF (en el artículo Ejemplo del Plan de Requerimientos de Materiales (MRP) se detallan los elementos necesarios para desarrollar un MRP).

Determine cuándo y en qué cantidades deben ser realizados los pedidos del computador ManBook. Para determinar el tamaño de lote use la política del Costo Unitario Mínimo. Asuma que el costo unitario de mantener inventario es de $1,65 por semana, y el costo de hacer un pedido es de $1.000.

Ejercicio Resuelto MRP (Plan de Requerimiento de Materiales)

En primer lugar resulta necesario identificar la estructura del producto final y cómo este se compone por distintos elementos de productos con demanda dependiente. En este caso en particular se dispone de 2 productos finales o productos padres: ManBook y ManBook Pro, cada uno de los cuales dispone de un chip M4 en su interior. La lista de materiales o BOM (Bill of Materials) se presenta a continuación:

Es decir, cada uno de los productos finales, a saber, ManBook y ManBook Pro, necesitan una unidad del chip M4 para ser fabricados.

Luego con esta información desarrollamos las políticas de lotificación para cada producto final y su insumo común (chip M4). Los resultados se resumen a continuación:

En primer lugar consideramos las necesidades brutas del producto ManBook. En el Registro del Inventario (IRF) se detalla que se dispone de un inventario inicial de 500 unidades y que no se considera mantener inventario de seguridad para dicho producto. En consecuencia, el saldo disponible proyectado (esto es el inventario al final de una semana) para la semana 1 es de 300 unidades que corresponde a descontar 200 unidades (necesidad bruta) al inventario inicial. En la semana 2 existe una entrada programada de 620 unidades (notar la diferencia entre una entrada programada y una entrada de pedido planeada). De esta forma el inventario (saldo disponible proyectado) al final de la semana 2 será de 720 unidades (300 unidades que vienen de la semana 1 + 620 de entradas programas en la semana 2 – 200 unidades de necesidad bruta de la semana 2). Las 720 unidades disponibles al final de la semana 2 permiten satisfacer los requerimientos brutos de las semanas 3, 4 y 5, quedando 50 unidades de saldo al final de la semana 5. Luego la necesidad neta de la semana 6 es de 190 unidades (240 unidades de necesidad bruta – 50 unidades del saldo disponible proyectado para la semana 5).

Se puede observar por tanto que las necesidades netas de Manbook son a contar de la semana 6 y a partir de este momento comenzamos a agrupar las necesidades utilizando la política de lotificación denominada Costo Unitario Mínimo (se recomienda revisar otras alternativas de lotificación descritas en el artículo Ejemplo de la Planeación de Requerimientos de Materiales (MRP o Material Requirements Planning)). El detalle del procedimiento se presenta a continuación:

Considerar un pedido por 190 unidades para satisfacer la necesidad neta exacta de la semana 6 (lo cual no genera costos de almacenamiento o inventario pero sí un costo de emisión de pedido de $1.000). El costo total incurrido ($1.000) se divide por el tamaño del pedido (190 unidades) siendo el costo unitario de $5,263.
Agrupar las necesidades de las semanas 6 y 7 y hacer un pedido por 410 unidades (190+220). El costo de emisión de pedido se mantiene en $1.000, no obstante el costo de almacenamiento será de $363 (se almacenan 220 unidades al final de la semana 6 a un costo unitario de almacenamiento semanal de $1,65). El costo unitario es $3,324 ($1.363/410).
Realizar un pedido único por 640 unidades (190+220+230). El costo de almacenamiento es $1.122 (se almacenan 450 unidades al final de la semana 6 y 230 al final de la semana 7, es decir, (450+230)*$1,65). El costo de emisión de $1.000 es fijo por pedido independiente del tamaño del pedido. En consecuencia el costo unitario será de $3,316 ($2.122/640) el cual corresponde al primer (y único en este ejemplo) costo unitario mínimo. Se concluye que se debe realizar un pedido de 640 unidades para satisfacer las necesidades netas exactas de la semana 6 a la semana 8, el cual se emite en la semana 5 dado un tiempo de reposición o lead time de 1 semana.

Continuando con el análisis ahora es el turno de planificar los requerimientos del producto final ManBook Pro y el chip M4. Para favorecer la lectura de nuestros usuarios incluimos nuevamente la tabla resumen del resultado del MRP.

Luego en el caso del producto ManBook Pro es de Tamaño Fijo de Pedido de 350 unidades (según lo descrito en el Registro del Inventario). El inventario disponible al final de la semana 1 para dicho producto es de 280 unidades correspondientes al inventario inicial – el inventario de seguridad – la necesidad bruta de la semana 1. En este contexto resulta intuitivo observar que la primera necesidad neta es para la semana 4 por 140 unidades (150-10, siendo las 10 unidades el saldo disponible proyectado al final de la semana 4). Por tanto se requiere la recepción de un pedido planeado por 350 unidades al inicio de la semana 4 el cual se emite con 2 semanas de antelación dado el tiempo de producción. De esta forma el inventario al final de la semana 4 será de 210 unidades lo cual satisface a la vez las necesidades brutas de las semanas 5 y 6. Finalmente se requiere la entrada de un nuevo pedido planeado por 350 unidades en la semana 7, siendo éste emitido en la semana 5.

Finalmente es necesario considerar las necesidades del chip M4. Notar que las necesidades brutas corresponderán a la suma de los requerimientos semanales de 100 unidades para ofertar a los servicios técnicos (según se detalla en el enunciado) más lo que corresponda como necesidad para la fabricación de los productos Manbook y Manbook Pro. Por ejemplo, en la semana 5 existe una necesidad bruta de 1.090 chips (640 para la fabricación de Manbook + 350 para la fabricación de Manbook Pro + 100 unidades para servicio técnico).

Adicionalmente se puede apreciar que el inventario disponible del chip M4 es suficiente para cubrir los requerimientos de la semana 1 a la semana 4, observándose necesidades netas en la semana 5 y 6 las cuales son cubiertas con pedidos de 1.000 unidades (el chip M4 al igual que el producto ManBook Pro utilizan la política de lotificación de Tamaño Fijo de Pedido) emitidos en las 3 y 4, respectivamente, dado un lead time de 2 semanas.

Evaluación de Proveedores y Determinación del Tamaño Óptimo de Pedido utilizando EOQ con Descuentos

El siguiente artículo representa la evaluación de 2 proveedores que ofrecen un esquema de descuentos por cantidad por las unidades vendidas, asumiendo que se satisfacen los supuestos simplificadores del modelo de Cantidad Económica de Pedido o EOQ. En particular consideraremos que la demanda del producto es constante y conocida y adicionalmente que el costo unitario de compra dependerá del tamaño del pedido (en este sentido utilizaremos el modelo de Cantidad Económica de Pedido (EOQ) con Descuentos por Cantidad).

Ejemplo EOQ con Descuentos

Una compañía necesita comprar controles remotos y tiene una demanda semestral de 4.800 unidades. Los controles pueden ser comprados o del proveedor A o del B. Los precios por cantidad de cada proveedor están en la tabla abajo:

El costo por pedido es de $30 para cualquiera de los proveedores y el costo anual de inventario es 25% del costo unitario. Adicionalmente la compañía incurre en un costo fijo por emitir un pedido de $10 por concepto de gastos administrativos. ¿De cuál proveedor la compañía debe comprar y cuál es el tamaño del pedido si el objetivo es minimizar costos totales anuales?.

En primer lugar determinamos el tamaño de pedido para cada uno de los tramos de descuentos por cantidad que aplican al Proveedor A. Notar que se considera una demanda anual de 9.600 controles remotos (un año tiene 2 semestres). Para el tramo 1 el pedido se aproxima a la cota superior de dicho intervalo; para el tramo 2 se mantiene el lote obtenido dado que pertenece al intervalo de [200,499] y en el tramo 3 se aproxima el tamaño de pedido a la cota inferior del intervalo (500 unidades) lo cual permite acceder a un precio unitario de $13,60.

En consecuencia los candidatos a óptimo son pedidos de 199, 472 y 500 unidades para el Proveedor A. Para ver cuál de ellos reporta el menor costo total anual se evalúa en la función de costos totales:

El tamaño óptimo de pedido en caso de seleccionar el Proveedor A es de 500 unidades por pedido.

En el caso del Proveedor B el procedimiento es similar al descrito para el Proveedor A. En este caso los candidatos a óptimo son pedidos de 149, 349 y 474 unidades.

Al evaluar en la función de costos totales (anual) se observa que el tamaño de lote que minimiza los costos para el Proveedor B son 474 controles por pedido.

Finalmente se procede a comparar los costos mínimos para cada proveedor con lo cual se concluye que se debe comprar al Proveedor A y hacer pedidos de 500 controles, alcanzando un costo total anual de $132.178 (que incluye los costos que se incurren anualmente por concepto de compra, emisión de pedidos y almacenamiento).