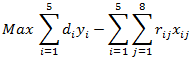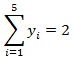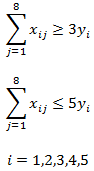programación de trabajos Archivos - Gestión de Operaciones

Regla de la Razón Crítica

La Regla de la Razón Crítica (conocido en inglés por CR o Critical Ratio) es una heurística que permite la secuenciación de trabajos en una máquina. El criterio que establece la Regla de la Razón Crítica es que los trabajos se deban procesar en orden creciente de acuerdo al cuociente ente el tiempo que falta a la entrega y el tiempo de proceso (recomendamos al lector revisar el artículo Reglas de Prioridad para la Programación de n Trabajos en una Máquina donde se detalla a través de un ejercicio resuelto la aplicación de otras heurísticas típicas de la programación de operaciones).

En este contexto la fórmula para el cálculo del ratio crítico es:

Ejemplo Regla de la Razón Crítica (Ratio Crítico)

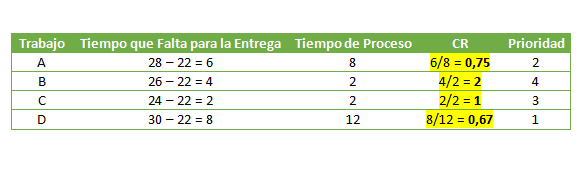
Hoy es el día 22 en un centro de trabajos y 4 trabajos están esperando ser atendidos en una máquina. La máquina puede procesar sólo un trabajo a la vez. Determine el ratio crítico para cada trabajo y establezca un ranking de prioridad para su procesamiento.

Por ejemplo, el trabajo A tiene como fecha de entrega el día 28 y requiere 8 días de proceso en la máquina.

Utilizando la Regla de la Razón Crítica los trabajos deben ser asignados en la siguiente secuencia: D, A, C, B. Se puede observar que sólo el trabajo B tiene holgura (esto debido a que su CR es mayor a 1). Por otra parte los trabajos A y D tienen ratios críticos menores a 1, lo cual significa que dichos trabajos no serán terminados a tiempo a menos que sean apurados. Finalmente el trabajo C tiene un ratio crítico igual a 1 que implica que podría ser terminado a tiempo en la medida que sea el primer trabajo en ser considerado en la secuencia (situación que no es la que ocurre en este caso).

Cabe recordar que los resultados propuestos al utilizar distintas reglas de prioridad deben ser analizados en virtud de su desempeño y en lo general no existe una regla que garantice el mejor desempeño en todos los aspectos.

Método de Johnson (Ejercicio Resuelto)

El Método de Johnson permite determinar una secuencia u orden para realizar trabajos en un taller que considera 2 máquinas, donde todos los trabajos siguen un orden común (por ejemplo, primero se ejecutan labores en una máquina 1 y luego en una máquina 2), asumiendo que todos los trabajos se encuentran disponibles para su programación al inicio del horizonte de evaluación y que los tiempos requeridos para pasar por cada máquina son conocidos (es decir, se asume que no existe incertidumbre). De esta forma se busca determinar el tiempo mínimo para completar los trabajos en el taller lo cual se conoce como makespan. En este contexto a continuación se presenta un ejemplo resuelto del Método o Algoritmo de Johnson.

Ejercicio Resuelto del Método de Johnson

Una imprenta se dedica a la copia y encuadernación de documentos. Esta mañana recibió los trabajos que se muestran a continuación, todos los cuales requieren ambas operaciones en ese orden:

La imprenta comienza a trabajar puntualmente a las 09:00 y no se detiene hasta que termina de procesar todos los trabajos. La hora de entrega para todos los trabajos corresponde a las 13:00. Determine una secuencia de manera que el tiempo que tardan en ser procesados los trabajos sea el menor posible, esto es minimizando el makespan. Construya una Carta Gantt para complementar su respuesta.

Este problema trata de máquinas en paralelo sin interrupción con trabajos cuyo tiempo de proceso es determinista y la llegada al comienzo (estática), de modo que se puede aplicar el Algoritmo de Johnson.

El tiempo más breve corresponde al trabajo A en encuadernación, por tanto se asigna en primer lugar y se ejecuta al final de la secuencia. Luego el tiempo más breve es para el trabajo B en encuadernación, siendo este trabajo asignado en segundo lugar y ejecutado penúltimo. De los trabajos remanentes el tiempo más breve es 40[min] existiendo un empate en encuadernación (trabajo C) y copia (trabajo E). En caso de empate el Método de Johnson establece que se prioriza la máquina 1 (en este caso copia) y por tanto E se asigna en tercer lugar y se ejecuta primero. A continuación naturalmente se asigna el trabajo C en cuarto lugar y se ejecuta antepenúltimo. El quinto trabajo en asignar será el D el cual se realiza inmediatamente antes del trabajo C (al tener su menor tiempo en encuadernación). Finalmente se asignan los trabajos F y G (en ese orden) ejecutándolos en segundo y tercer lugar, respectivamente. De esta forma la secuencia es:

E-G-F-D-C-B-A

El makespan para este problema de Programación de Trabajos es de 440 minutos, terminando de atender el último trabajo a las 16:20.

En relación a los resultados obtenidos anteriormente determine: ¿A qué hora se termina de atender el último trabajo?, ¿Cuántos trabajos atrasados tiene la imprenta?, ¿Cuál es el tiempo de flujo promedio?, ¿Cuál es el atraso promedio?, ¿Cuál es el atraso máximo?.

Para responder a esta pregunta confeccionamos una tabla resumen la cual se basa en los resultados obtenidos a través de la Carta Gantt y los horarios de entrega de los trabajos.

Total Atrasos: 5 (Trabajos A, B, C, D y F)
El último trabajo se termina de atender a las 16:20 (Trabajo A)
Tiempo de Flujo Promedio: 06:01
Atraso Promedio: 1:48
Atraso Máximo: 3:20

Cabe recordar que el Tiempo de Flujo (TF) corresponde al tiempo total que cada trabajo se encuentra en el taller, es decir, esto es la suma del tiempo de espera más el tiempo de atención o procesamiento en las distintas máquinas. Por ejemplo si bien el trabajo A requiere en total un tiempo de 30[min] éste comienza a ser atendido recién a las 15:20 en copia, terminando a las 16:20 en encuadernación (total 60[min] o 1[hora]). Adicionalmente el trabajo A debe esperar 7 horas con 5 minutos (es decir, de las 08:15 a las 15:20) para comenzar su atención en copia. Luego el Tiempo de Flujo es 1:00+7:05=8:05 (8 horas y 5 minutos).

Cómo enfrentar una Solución Infactible obtenida con el Método Húngaro

En algunos casos los ceros que se producen en los Pasos 1 y 2 del Método Húngaro no producen una solución factible en forma directa, es decir, la asignación alcanzada es infactible. En este caso se necesitan más pasos para alcanzar la asignación óptima (factible). Para ilustrar esta situación consideremos el siguiente ejemplo que consiste en la asignación a costo mínimo de 4 ingenieros a 4 tareas, donde cada ingeniero debe desempeñar exactamente una tarea:

Al aplicar los Pasos 1 y 2 del Método Húngaro se obtiene la siguiente matriz reducida:

Notar que los elementos cero (marcados con color azul) no permiten asignar una tarea por ingeniero. Por ejemplo, si se asigna el ingeniero 1 a la tarea 1, se eliminará la columna 1, y el ingeniero 3 no tendrá elemento cero en las tres columnas restantes. Para solucionar este obstáculo se agrega el siguiente paso al procedimiento:

Paso 2a: Si no se puede asegurar una asignación factible (con todos los elementos cero) con los Pasos 1 y 2.

Trazar la cantidad mínima de líneas horizontales y verticales en la última matriz reducida que cubran todos los elementos cero.
Seleccionar el elemento mínimo no cubierto, restarlo de todo elemento no cubierto y a continuación sumarlo a todo elemento en la intersección de dos líneas.
Si no se puede encontrar una asignación factible entre los elementos cero que resulten, repetir el Paso 2a. En caso contrario, seguir en el Paso 3 para determinar la asignación óptima.

Al aplicar el Paso 2a a la matriz reducida presentada anteriormente, se obtienen las celdas color amarillo según se aprecia a continuación:

La celda de valor mínimo sin fondo amarillo es igual a $1 (destacada con color rojo). Este elemento se resta de todas las celdas sin fondo amarillo y se suma a a las celdas de las intersecciones (destacadas con color azul).

La solución óptima (por cierto factible) se ha marcado con fondo azul: el ingeniero 1 realiza la tarea 1, el ingeniero 2 la tarea 3, el ingeniero 3 la tarea 2 y el ingeniero 4 la tarea 4 . El costo total (valor óptimo) de esta asignación es $1+$10+$5+$5=$21.

El Método Húngaro como Algoritmo de Solución del Modelo de Asignación

Un caso típico de un modelo de asignación es aquel que considera la asignación de trabajadores de distintos niveles de capacitación a puestos de trabajo. Naturalmente un puesto que coincide con los conocimientos de un trabajador cuesta menos que uno en el que el trabajador no es tan hábil. El objetivo del modelo es determinar la asignación de costo mínimo de trabajadores a puestos.

Consideremos un problema con n trabajadores que deben ser asignados a n puestos de trabajo. Sea $x_{ij}$ el costo de asignar al trabajador i al puesto j. Asumamos adicionalmente que cada trabajador debe realizar exactamente un trabajo. Notar que no existe pérdida de generalidad en asumir que la cantidad de trabajadores es igual a la cantidad de puestos, porque siempre se pueden agregar trabajadores o puestos ficticios para obtener esa condición.

El Método Húngaro consta de los siguientes pasos:

Paso 1: En la matriz original de costo, identificar el mínimo de cada fila y restarlo de todos los elementos de la fila.

Paso 2: En la matriz que resulte del Paso 1, identificar el mínimo de cada columna, y restarlo de todos los elementos de la columna.

Paso 3: Identificar la solución óptima como la asignación factible asociada con los elementos cero de la matriz obtenida en el Paso 2.

A continuación presentaremos un ejemplo que muestra la aplicación del Método Húngaro que nos permite decidir la asignación de trabajadores a puestos de trabajo.

Ejemplo Método Húngaro

Un equipo de 3 ingenieros debe ser asignado para la realización de 3 tareas, donde cada ingeniero debe hacer una tarea. Se requiere encontrar la asignación de costo mínimo para lo cual se dispone de los costos asociados a que el ingeniero i realice la tarea j. Por ejemplo, $c_{11}=15$ representa el costo correspondiente a que el ingeniero 1 asuma la tarea 1.

Aplicar el Método Húngaro para encontrar una asignación óptima de los ingenieros a las tareas.

El Paso 1 del Método Húngaro requiere identificar el valor mínimo de cada fila. En el caso de la fila 1 dicho valor es $9 siendo el costo de que el ingeniero realice la tarea 3. En particular si se dispone de un problema de mayor tamaño, hacer uso de Excel facilita los cálculos tal como se muestra en la siguiente imagen:

A continuación se resta el mínimo de cada fila a cada uno de los valores de la fila respectiva, para obtener la matriz reducida:

La aplicación del Paso 2 produce los mínimos de cada columna según se observa en la tabla anterior. Al restar esos valores de las columnas respectivas se obtiene la siguiente matriz reducida:

Las celdas con valor cero y color azul son la solución óptima. En consecuencia el ingeniero 1 realiza la tarea 2, el ingeniero 2 asuma la tarea 1 y el ingeniero 3 la tarea 3. Cada ingeniero realiza exactamente una tarea y el costo total de dicha asignación (valor óptimo) es de $9+$10+$8=$27. Los pasos presentados del Método Húngaro para el ejemplo anterior funcionaron bien debido a que los elementos cero de la matriz anterior permite una asignación factible de ingenieros a tareas (en el sentido que las tareas se asignan de forma única a los ingenieros). No siempre esto es posible lograr una solución factible en la aplicación caso en el cual se requiere pasos adicionales para la aplicación del método.

Conformación de Equipos de Trabajo a través de la Programación Entera

La Programación Entera provee una alternativa metodológica para enfrentar los Problemas de Asignación en donde una serie de recursos (mano de obra, horas máquinas, materia prima, etc) se deben asignar a uno o más fines (conformar equipos de trabajo, producción, etc). El siguiente artículo aborda el problema que enfrenta una consultora que debe formar 2 equipos de expertos del área de operaciones en base a 8 ingenieros industriales. Estos 2 equipos los puede escoger de entre 5 equipos de profesionales que trabajan en la consultora. Los datos del problema se muestran en la siguiente tabla:

Cada equipo tiene que estar compuesto por al menos 3 y a lo más 5 expertos. Si el profesional j es asignado al equipo i, la compañía le debe pagar una remuneración rij. Si en la tabla aparece un guion (—), significa que el experto no puede ser asignado a ese equipo: por ejemplo, el profesional 3 no puede pertenecer al equipo 2 ni al 4. Se espera que el equipo i genere un ingreso di.

Se requiere formular y resolver computacionalmente un modelo de optimización que permita determinar la conformación de los equipos, alcanzando la utilidad máxima y cumpliendo las condiciones anteriormente expuestas. Definir claramente las variables de decisión, función objetivo y restricciones.

Variables de Decisión:

Función Objetivo:

Restricciones:

Sólo 2 equipos se seleccionan:

Cada equipo está formado solamente por entre 3 y 5 expertos:

A continuación se presenta un extracto de la implementación computacional del problema de conformación de equipos de trabajo con Solver. Notar que aquellas combinaciones infactibles en términos de asignación de ingenieros a equipos ha sido marcado con color rojo y en particular se le ha asignado un costo significativamente mayor en comparación a aquellas asignaciones factibles. De esta forma se espera que estos casos no sean seleccionados (por cierto también se puede seleccionar paso a paso sólo las celdas factibles al momento de definir las variables de decisión en Solver, omitiendo las situaciones infactibles).

La solución óptima consiste en seleccionar el equipo 1 y 5. En la tercera tabla (filas 16 a 21) se muestra la asignación de ingenieros a dichos equipos (por supuesto aquellos equipos que no se conforman, es decir, equipos 2, 3 y 4 no tienen ingenieros asignados). El equipo 1 se compone de los ingenieros 1, 3 y 4; por otra parte el equipo 5 se compone de los ingenieros 1, 3 y 10. Notar que no existe incentivo económico a conformar equipos con un mayor número de integrantes. Finalmente el valor óptimo (utilidad máxima) es de $16.550.

¿Quieres tener el archivo Excel con la resolución en Solver de este problema?. Recomiéndanos en Facebook, Google+ o Twitter utilizando la herramienta de redes sociales a continuación y accede de forma gratuita e inmediata a la descarga del archivo (el enlace de descarga con el nombre “Descarga el Archivo” se mostrará abajo una vez que nos hayas recomendado).

[l2g name=»Descarga el Archivo» id=»4545″]