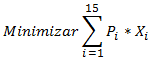En el artículo anterior abordamos una aplicación clásica de la Programación Entera conocida como el Problema de Corte de Rollos («Cutting Stock Problem») el cual en esta oportunidad resolveremos utilizando la versión Premium de Solver. Si bien el tamaño y complejidad del modelo permitiría enfrentar su resolución sin mayores inconvenientes con la versión tradicional de Solver, utilizaremos Premium Solver Pro para efectos ilustrativos del uso de esta herramienta mejorada.
En este contexto recordemos las características del modelo de optimización de corte de rollos que consiste en minimizar una función de pérdida de material sujeta a restricciones que permiten satisfacer la demanda de rollos de menor tamaño y que incluye adicionalmente condiciones de no negatividad e integralidad para las variables de decisión:
- 2X1+X2+X3+X8+X9+X13>=150
- X2+3X4+2X5+X6+X8+2X10+X11+X14>=200
- X2+3X3+2X5+3X6+5X7+X9+X10+2X11+4X12+X14+3X15>=175
- Xi>=0 Enteros (i=1,…,15)
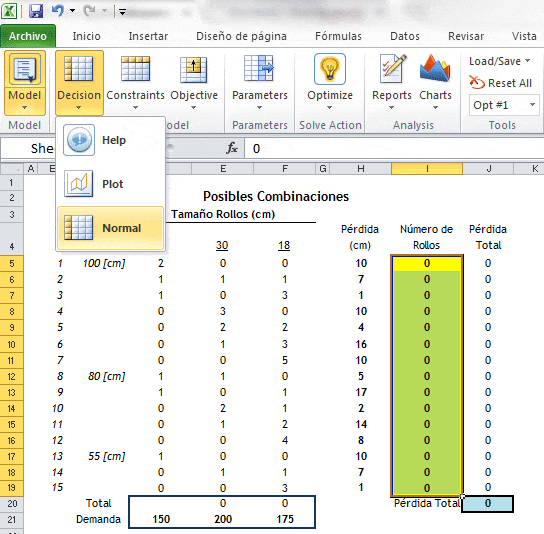
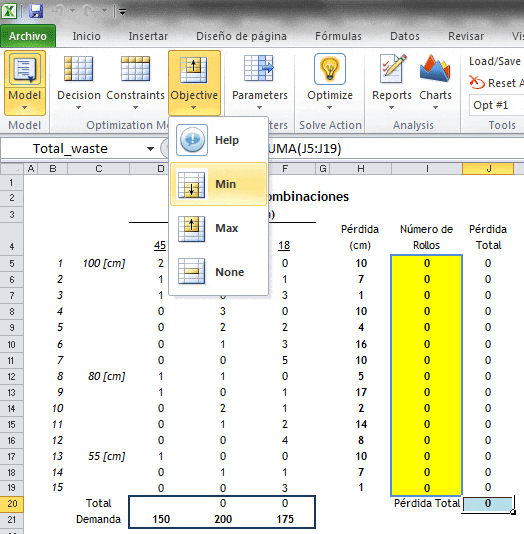
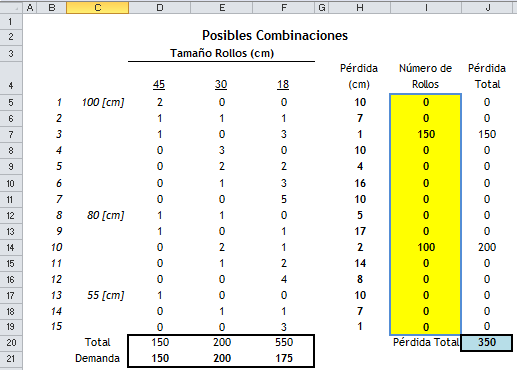
Con el objetivo de implementar en Premium Solver Pro el problema anterior creamos en Excel una estructura que resuma la información del problema y que facilite su resolución. La imagen a continuación considera en las celdas con color amarillo las variables de decisión (15 variables) y en la celda J20 (color celeste) la función objetivo.
A continuación para definir las variables de decisión seleccionamos «Decision» y luego «Normal». Notar que previamente se ha seleccionado el rango de celdas que queremos definir como variables de decisión (en este ejemplo las 15 celdas en color amarillos).
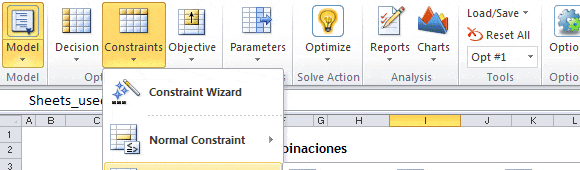
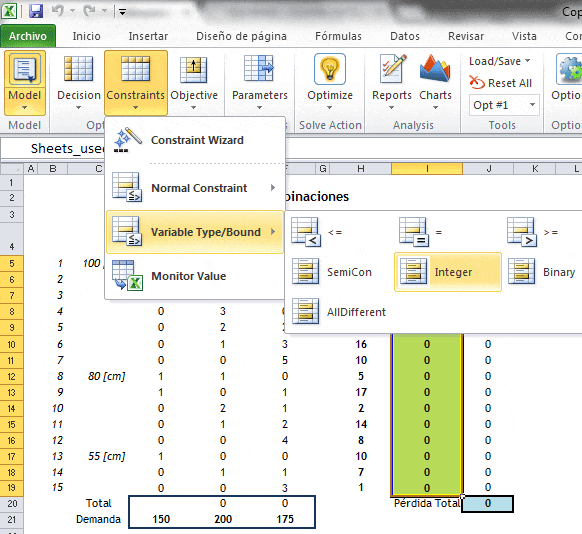
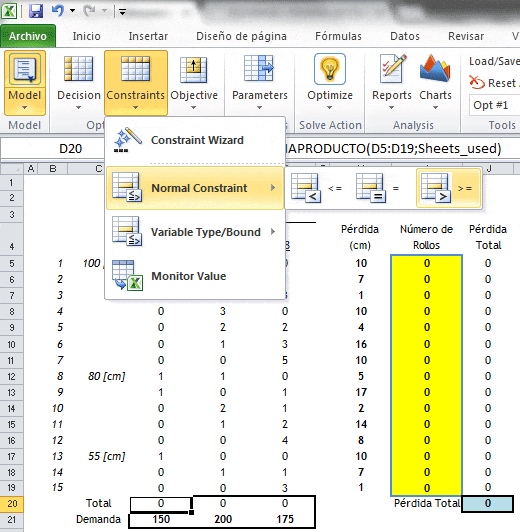
Para restringir el valor que adopten las variables de decisión a números enteros se debe ir a «Constraints», «Variable Type/Bound», «Integer» como muestra la siguiente imagen:
Ahora nos posicionamos en la celda J20 que contiene la función objetivo (esta celda contiene una fórmula que es la sumaproducto de la pérdida de material en [cm] asociada a cada patrón de corte ponderada por la cantidad de veces que se utiliza un esquema de corte definido). Luego en «Objective» seleccionamos «Min».
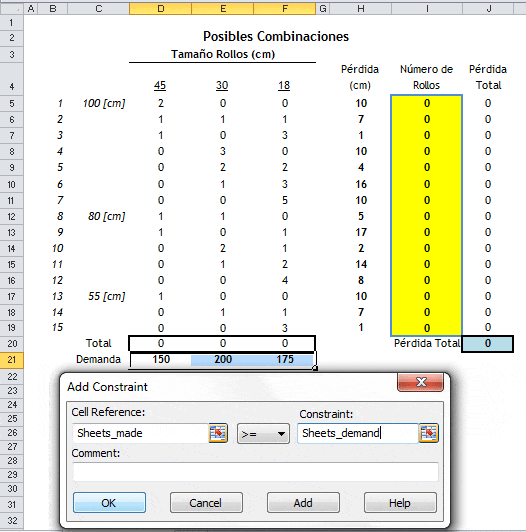
En el siguiente paso corresponde incorporar las restricciones de demanda para el problema. Notar que dado que las restricciones de demanda de rollos de 45[cm], 30[cm] y 18[cm] son todas del tipo «>=» las podemos incorporar todas de forma simultanea tal se muestra a continuación:
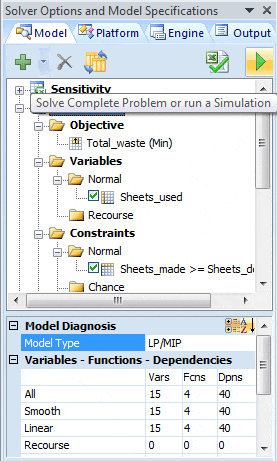
Finalmente estamos en condiciones de poder resolver el modelo de optimización con Premium Solver Pro. A la derecha de la planilla de cálculo encontraremos la interfaz del programa que resume las características del problema que hemos implementado.
Seleccionamos el icono con flecha verde que esta en la esquina superior derecha de la imagen anterior para resolver el modelo, obteniendo la solución óptima y valor óptimo que se muestra a continuación:
La solución óptima consiste en utilizar 150 veces el patrón de corte 3 (X3=150) y 100 veces el patrón de corte 10 (X10=100), omitiéndose el uso de los otros esquemas de corte. Con esto la pérdida de material (total) asciende a 350[cm] de papel, logrando satisfacer la demanda para cada tipo de rollo (notar que para el caso de los rollos de 18[cm] se producen 550[u] siendo la demanda de 175[u]). En nuestro canal de Youtube puedes revisar la implementación y resolución computacional del modelo anterior.