Una línea aérea está considerando incorporar vuelos desde y hacia su aeropuerto base y por lo tanto necesita contratar más agentes de servicio al cliente. Sin embargo, no está claro cuántos más debe contratar. La administración reconoce la necesidad de controlar el costo y al mismo tiempo brindar un nivel de atención satisfactorio. Se ha realizado un análisis del número mínimo de agentes de servicio que deben encontrarse de guardia en diferentes momentos del día para proporcionar un nivel satisfactorio de servicio.
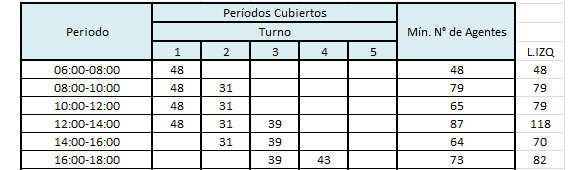
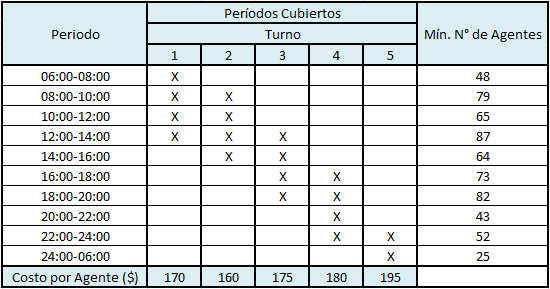
Se ha acordado que cada agente trabaje un turno de 8 horas en los turnos mostrados en la tabla anterior. Por ejemplo, el turno 3 va desde las 12:00 hasta las 20:00. Los sueldos de cada turno son diferentes debido a que unos son más deseables que otros. Por ejemplo, a cada agente que cumpla el turno 3 debemos pagarle diariamente $175.
Se busca formular y resolver un modelo Programación Entera que permita a la línea aérea encontrar el plan de asignación de agentes al menor costo posible y que cumpla los requerimientos impuestos.
1. Variables de Decisión: Establecer un plan de asignación de agentes a los distintos turnos de trabajo.
Xi: Número de Agentes asignados al Turno i con i=1,2,3,4,5 con Xi>=0 {Enteros}
2. Función Objetivo: Minimizar el costo total de la asignación de agentes.
Minimizar 170X1+160X2+175X3+180X4+195X5
3. Restricciones: Se busca garantizar que en cada período del día se cuenta con la cantidad mínima de agentes requeridos.
- X1 >= 48
- X1 + X2 >= 79
- X1 + X2 >= 65
- X1 + X2 + X3 >= 87
- X2 + X3 >= 64
- X3 + X4 >= 73
- X3 + X4 >= 82
- X4 >= 43
- X4 + X5 >= 52
- X5 >= 25
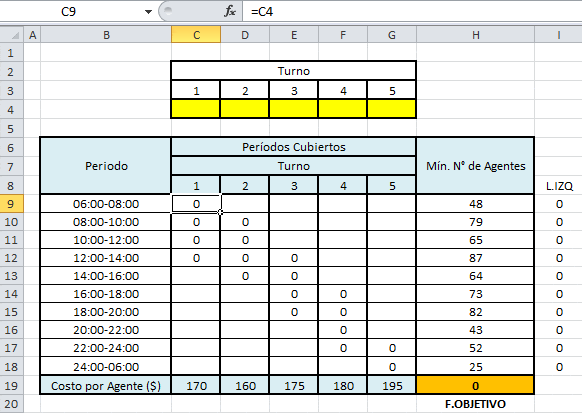
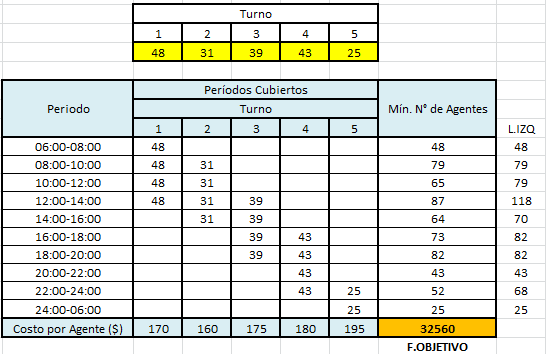
A continuación implementamos el modelo anterior en Solver. Notar que las celdas color amarillo son las asignadas a las variables de decisión y éstas a la vez vinculan las combinaciones posibles entre turnos y períodos atendidos.
Adicionalmente en la columna I se ha guardado el valor del lado izquierdo de las restricciones que garantizan el mínimo número de agentes por período.
Finalmente la función objetivo (celda color naranjo) corresponde a la suma producto entre las variables de decisión y los parámetros que representan el costo diario por agente en los respectivos turnos (SUMAPRODUCTO(C4:G4;C19:G19)).
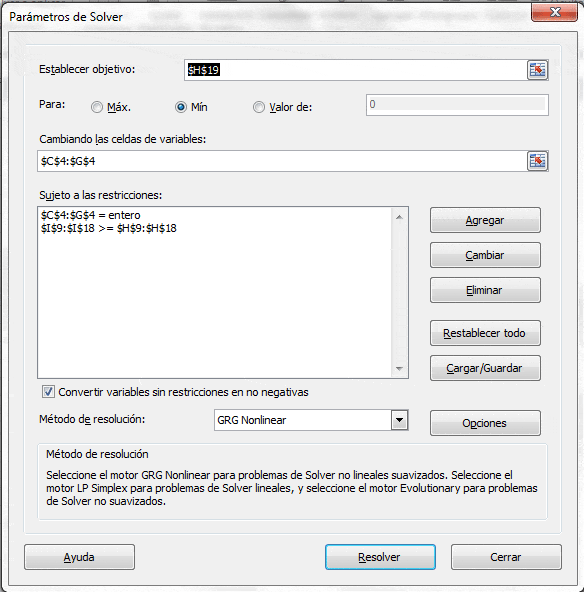
La implementación del modelo anterior en la interfaz de Solver es la siguiente:
Alcanzando la solución óptima del problema que considera la asignación de 48, 31, 39, 43 y 25 personas a los turnos 1,2,3,4 y 5, respectivamente, con un costo total (mínimo) de $32.560.
El siguiente video de nuestro canal en Youtube muestra la resolución del problema anterior:
¿Quieres tener el archivo Excel con la resolución en Solver de este problema?.
[sociallocker]Descargar Aquí Problema Agentes Call Center[/sociallocker]