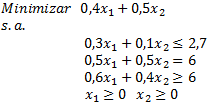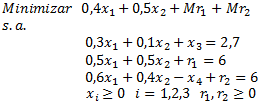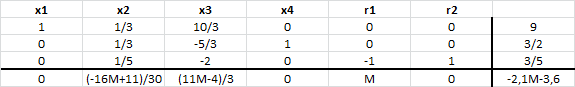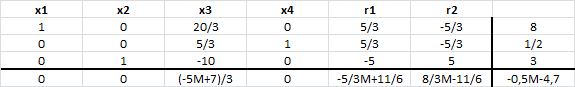En el contexto de la aplicación del Método Simplex no siempre es inmediata la obtención de una solución básica factible inicial, en las variables originales del modelo. Para conseguir esto existen varios procedimientos como son el Método Simplex de 2 Fases y el Método de la M Grande (o Gran M) el cual abordaremos en este artículo. Para ello consideremos el siguiente modelo de Programación Lineal en 2 variables:
A continuación agregamos las variables no negativas (holgura restricción 1),
(auxiliar restricción 2),
(exceso restricción 3) y
(auxiliar restricción 3). El modelo ahora es:
Donde el parámetro M es una constante positiva suficientemente grande para representar una penalización adecuada en la función objetivo. La tabla inicial del método esta dada por:
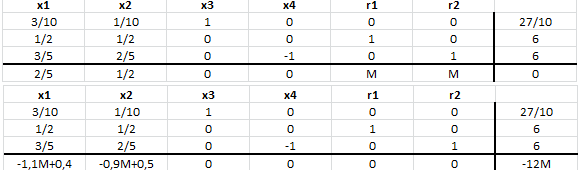
Antes de continuar con las iteraciones se debe procurar que el costo reducido de las variables y
sean ceros. Para ello multiplicamos por -M la fila 2 y la fila 3 y luego sumamos a la fila 4, obteniendo lo siguiente:
Ahora debemos seleccionar que variable no básica ingresa a la base. El menor costo reducido corresponde a la variable en consecuencia dicha variable ingresa a la base. Luego calculamos el mínimo cuociente en dicha columna:
, el cual se alcanza en la fila 1, por tanto la variable
deja la base. Se actualiza la tabla:
Siguiendo con las iteraciones ahora la variable entra a la base. El criterio de factibilidad indica que:
la variable
abandona la base (el pivote se encuentra en la fila 3). Actualizamos la tabla:
Una nueva iteración indica que ingresa a la base. El mínimo cuociente en la respectiva columna es:
(recordar que se omiten denominadores menores a cero). Ahora el pivote se encuentra en la fila 2 y en consecuencia
deja la base. Se actualiza la tabla:
Se ha alcanzado la solución óptima con y
. Notar que las variables auxiliares (r1 y r2) son no básicas en el óptimo. El valor óptimo es 21/4 (notar que el signo esta cambiado).
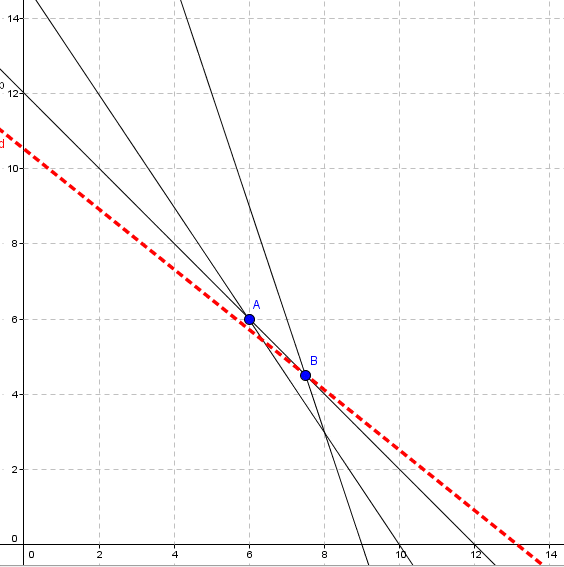
Para una mejor comprensión de los resultados alcanzados a continuación se presenta la resolución gráfica del problema haciendo uso del software Geogebra. El dominio de soluciones factibles corresponde a la recta que une los vértices A y B. Adicionalmente se muestra la curva de nivel que pasa por la solución óptima (vértice B).
Teóricamente se espera que en la aplicación del Método de la M Grande las variables auxiliares sean no básicas en el óptimo. Si el modelo de Programación Lineal es infactible (es decir, si las restricciones no son consistentes), la iteración del Método Simplex final incluirá al menos una variable artificial como básica.
Adicionalmente la aplicación de la técnica de la M Grande implica teóricamente que M tiende a infinito. Sin embargo al usar la computadora M debe ser finito, pero suficientemente grande. En específico M debe ser lo bastante grande como para funcionar como penalización, al mismo tiempo no debe ser tan grande como para perjudicar la exactitud de los cálculos del Método Simplex, al manipular una mezcla de números muy grandes y muy pequeños.