Un problema infactible en Programación Lineal es una situación que se detecta cuando en la aplicación del Método Simplex de 2 Fases el valor óptimo del problema de la Fase 1 es distinto a cero (para continuar a la Fase 2 se requiere que el valor óptimo de la Fase 1 sea cero). Cabe recordar que un problema infactible es aquel cuyo dominio de soluciones factibles es vacío.
Consideremos el siguiente modelo de Programación Lineal en 2 variables que nos permitirá representar dicha situación:
Agregamos las siguientes variables al modelo para aplicar el Método Simplex de 2 Fases: .
Definiendo el problema inicial de la Fase 1:
A continuación llevamos el costo reducido de la variable a cero, multiplicando por -1 la fila 2 y sumando ésta a la fila 3:
Para favorecer la rapidez de convergencia del método entra a la base. Luego calculamos el criterio del mínimo cuociente:
por tanto
deja la base. Actualizamos la tabla:
Notar que todas las variables no básicas tienen costos reducidos mayores o iguales a cero. Adicionalmente las variables básicas
cumplen con las condiciones de no negatividad. En consecuencia hemos finalizado la Fase 1 del Método Simplex de 2 Fases, sin embargo, el valor de la función objetivo es distinto de cero (en el ejemplo es -4) lo que determina que el problema es infactible.
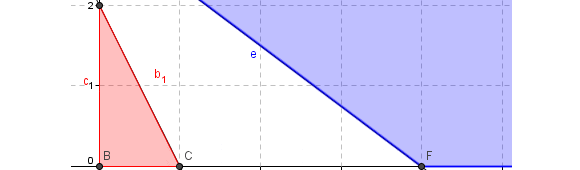
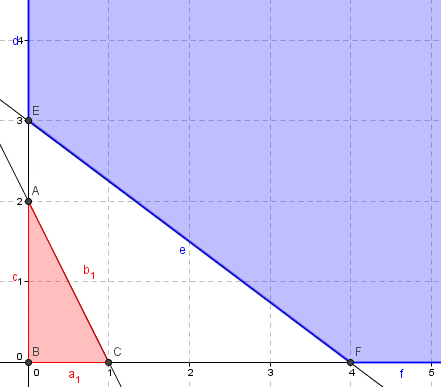
La siguiente representación gráfica del problema anterior se puede realizar con Geogebra. El área achurada color rojo corresponde a la intersección de los conjuntos de factibilidad definido por la restricción 1 y las de no negatividad. Por otra parte el área achurada color azul es la intersección de los conjuntos de factibilidad definido por la restricción 2 y las de no negatividad. Luego resulta evidente que la intersección de dichos conjuntos (rojo y azul) es vacío, por tanto no existen valores que puedan adoptar las variables de decisión y satisfacer de forma simultanea todas las restricciones del problema.
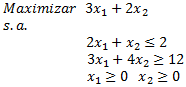
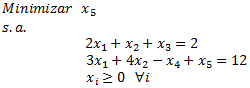
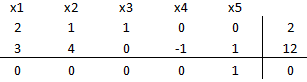
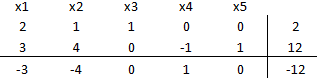
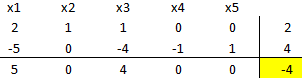
Excelente aporte estimados estaré revisando continuamente