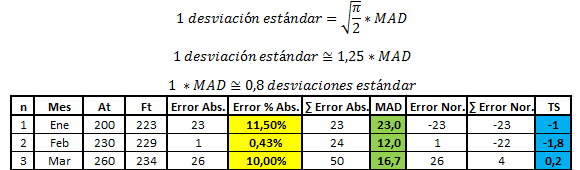
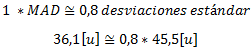El concepto de error en una proyección de demanda tiene que ver con la diferencia entre el valor real (observado) y el valor pronosticado. Esto da origen a errores de sobre estimación o sub estimación de la demanda real cuando dichos errores son negativos o positivos, respectivamente. En este contexto cuando los errores que ocurren en el pronóstico de demanda tienen una distribución normal (el caso más común) la Desviación Absoluta Media (MAD) se relaciona con la Desviación Estándar del Error (σ) de la siguiente forma:
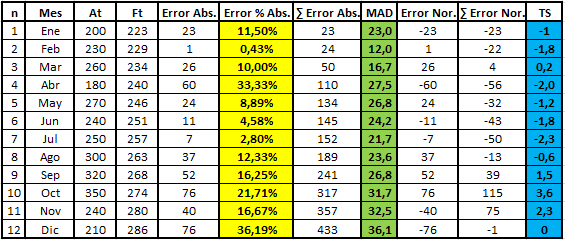
Para ilustrar sobre esta relación consideremos el ejemplo utilizado en el artículo donde calculamos el Error Porcentual Absoluto Medio (MAPE) cuyos pronósticos Ft se obtienen al ajustar una Regresión Lineal a los datos reales de la demanda.
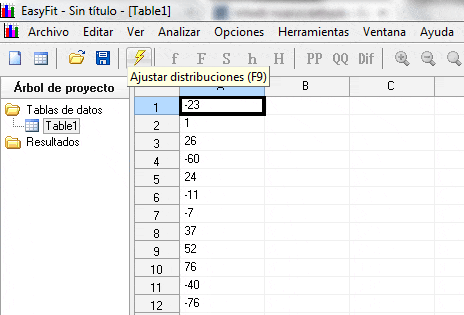
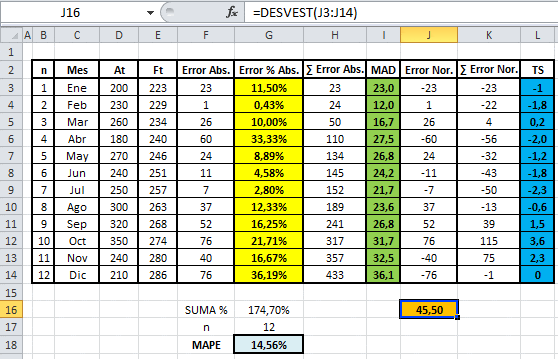
Notar que el MAD calculado a Diciembre es de 36,1[u]. Luego para corroborar el cumplimiento de la relación aproximada entre el MAD y σ se requiere verificar si los errores del pronóstico se distribuyen normal. Para esta evaluación utilizaremos el software Easyfit y su herramienta de ajuste de distribuciones. Es importante en este punto destacar que es deseable contar con más datos para realizar el ajuste, no obstante, nos interesa mostrar el procedimiento.
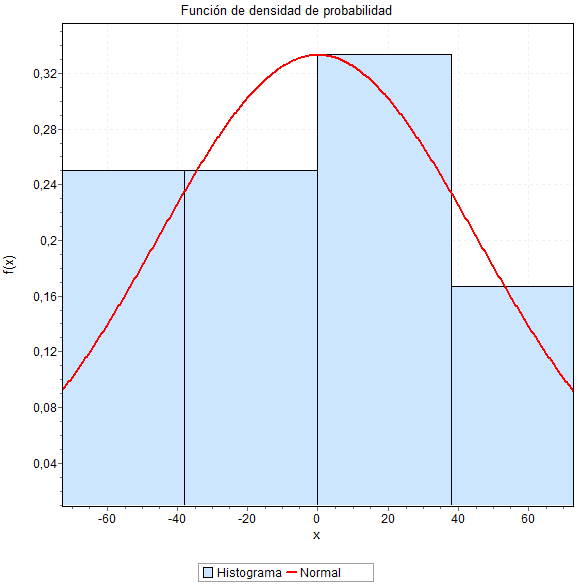
El programa nos entrega el siguiente histograma donde la curva de color rojo representa el comportamiento de una distribución normal (teórica). Adicionalmente en las estadísticas descriptivas se puede obtener que el error medio (considerando la naturaleza del signo del error) es -0,0833 (aproximado) lo cual constituye un elemento a favor de la relación que deseamos verificar.
Si volvemos a los resultados que da origen la planilla Excel podemos calcular la Desviación Estándar del Error σ (celda color naranjo) que es 45,50[u] a través de la fórmula =DESVEST(J3:J14).
Con estos resultados corroboramos si efectivamente 1 MAD es equivalente (aproximadamente) a 0,8 desviaciones estándar del error. La conclusión es que para los datos de este ejemplo dicha relación es efectiva (por cierto aproximada) por lo cual luego de verificar que los errores del pronóstico se distribuyen normal (razonablemente) bastaría con calcular el MAD para poder generar una estimación razonable de la desviación estándar del error (o viceversa).