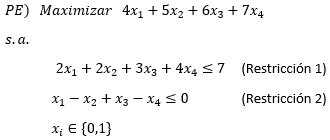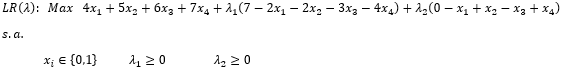Ejemplo de Relajación Lagrangeana en Programación Entera

El método de Relajación Lagrangeana (o Relajación Lagrangiana) consiste básicamente en un Método de Descomposición cuya idea se basa en descomponer un problema original restringido, en principio complejo de resolver, de modo de reemplazarlo por otro problema que permita simplificar la resolución. Esto se logra incorporando aquellas restricciones que se consideran difíciles (las que hacen compleja la resolución directa del problema) a la función objetivo, donde cada una de éstas tendrá asociada un Multiplicador de Lagrange $\lambda$ que permitirá (iterativamente) penalizar el incumplimiento de las mismas al ser establecidos distintos valores para los multiplicadores. De esta forma se espera que las restantes restricciones (las que no se incorporan mediante penalizaciones en la función objetivo) permitan verificar un problema cuya resolución sea fácil (o al menos más sencilla que el problema en su estructura original).

El problema asociado a encontrar los valores de $\lambda$ que permitan minimizar la función $LR(\lambda)$ (que en sí es un problema de maximización) se conoce como el Problema Dual Lagrangeano. En general puede resultar un problema tedioso de resolver, no obstante, a continuación se enumeran una serie de pasos que permiten una aproximación a la implementación del método de Relajación Lagrangeana.

Supongamos que el problema original es de Maximización y que la o las restricciones relajadas son inecuaciones del tipo $\leqslant$ :

Comenzar con cada $\lambda$ igual a cero. Definir inicialmente (y de forma arbitraria) un Paso de magnitud k.
Resolver $LR(\lambda)$ de modo de alcanzar la solución óptima en términos de x.
Para cada restricción violada por x, incrementar el correspondiente $\lambda$ por k.
Si han transcurrido m iteraciones desde que se alcanzo la última relajación para el problema dual lagrangeano, disminuir k a la mitad.
Ir al Paso 2.

Para ilustrar el procedimiento anterior consideremos un Problema de la Mochila como el que se describe a continuación:

Luego de resolver el problema de Programación Entera propuesto haciendo uso de Solver de Excel se alcanza la Solución Óptima: $x_{1}=0, x_{2}=0, x_{3}=1, x_{4}=1$ con Valor Óptimo: $V(PE)=13$ .

Relajaremos las Restricciones 1 y 2 incorporando éstas a la función objetivo y dejando exclusivamente las condiciones de binarios para las variables de decisión. Esto da origen a nuestro problema de Relajación Lagrangeana $LR(\lambda)$ :

Consideraremos inicialmente $\lambda_{1}=0$ y $\lambda_{2}=0$ . La resolución de dicha instancia es trivial obteniéndose como Solución Óptima: $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=1$ y Valor Óptimo: $LR(\lambda)=22$ . Notar que la solución alcanzada no satisface la Restricción 1 (sin embargo, se satisface la Restricción 2).

Penalizaremos la Restricción 1 al considerar $\lambda_{1}=0,5$ (penalización arbitrariamente definida como punto de partida) y manteniendo $\lambda_{2}=0$ (dado que la Restricción 2 se satisface). La Solución Óptima es $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=1$ con Valor Óptimo de $LR(\lambda)=20$ . En consecuencia, la penalización establecida resulto ser insuficiente para que se evitara la violación (incumplimiento) de la Restricción 1.

Sea $\lambda_{1}=1$ (aumentamos nuevamente en 0,5 la penalización de la Restricción 1) y $\lambda_{2}=0$ . La Solución Óptima se mantiene: $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=1$ con Valor Óptimo: $LR(\lambda)=18$ .

Sea $\lambda_{1}=1,5$ y $\lambda_{2}=0$ . La Solución Óptima se mantiene: $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=1$ con Valor Óptimo: $LR(\lambda)=16$ . Se sigue violando la Restricción 1.

Sea $\lambda_{1}=2$ y $\lambda_{2}=0$ . La Solución Óptima ahora es: $x_{1}=0, x_{2}=1, x_{3}=0, x_{4}=0$ con Valor Óptimo: $LR(\lambda )=15$ . Ahora se satisfacen las Restricciones 1 y 2, teniendo éstas holguras de 5 y 1, respectivamente. Luego si se decide disminuir la penalización de la Restricción 1 a $\lambda_{1}=1,5$ se vuelve al mismo punto de la iteración anterior. En consecuencia se disminuye la magnitud del paso (penalización) a 0,25 de modo que $\lambda_{1}=1,75$ y $\lambda_{2}=0$ . La Solución Óptima es: $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=0$ con Valor Óptimo: $LR(\lambda)=15$ .

No obstante, la Restricción 2 no se satisface para esta nueva solución y de esta forma se establecen nuevas penalizaciones: $\lambda_{1}=1,75$ y $\lambda_{2}=0,25$ y que dan origen a la Solución Óptima: $x_{1}=1, x_{2}=1, x_{3}=1, x_{4}=1$ con Valor Óptimo: $LR(\lambda)=15$ .

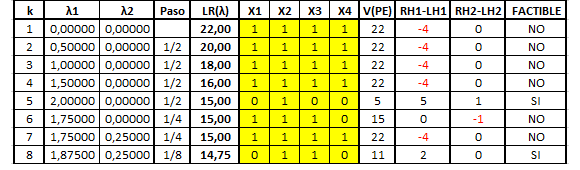
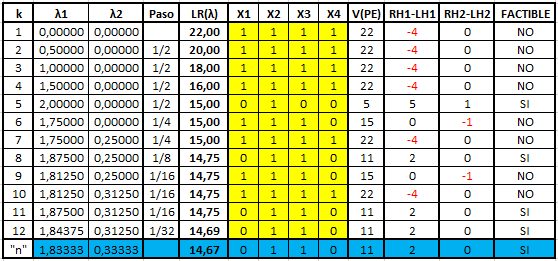
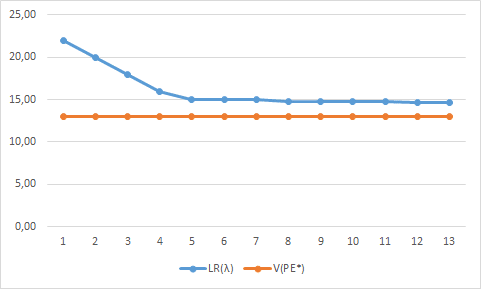
El procedimiento continua de esta forma disminuyendo la magnitud del paso (penalización) cuando resulta necesario. Notar que de esta forma las respectivas penalizaciones pueden aumentar o disminuir al cabo de una iteración. El detalle de las iteraciones realizadas se muestra a continuación:

Para cada iteración k se muestra la penalización aplicada para la Restricción 1 y 2 respectivamente, el criterio para la actualización del Paso, el valor de la función objetivo de la Relajación Lagrangeana $LR(\lambda )$ , la Solución Óptima alcanzada para el problema (destacado con color amarillo), el valor que representa dicha solución óptima al ser evaluada en la función objetivo original V(PE), la holgura de la Restricción 1 (2) (con color rojo se destaca cuando se viola la restricción en una determinada magnitud) y si la solución óptima alcanzada en la iteración k-ésima es factible en el problema original PE).

Según se señala en un tutorial por Michael A. Trick (donde se ha tomado este ejemplo y se ha extendido a un número mayor de iteraciones con ciertas variaciones en la aplicación de las mismas) las penalizaciones “óptimas” (luego de seguir iterando) corresponderán aproximadamente a $\lambda_{1}=1,83$ y $\lambda_{2}=0,33$ , alcanzando $LR(\lambda )=14,67$ que constituye una cota superior del valor óptimo del problema original. La Solución Óptima asociada a este escenario es $x_{1}=0, x_{2}=1, x_{3}=1, x_{4}=0$ que es factible en el problema original y reporta un valor en la función objetivo de 11. Notar que la Solución Óptima del PE) es $x_{1}=0, x_{2}=0, x_{3}=1, x_{4}=1$ con Valor Óptimo de 13.

Rating: 5.0/5. From 6 votes.

Please wait...

Deja una respuesta Cancelar la respuesta