El Problema de la Mochila (conocido también como Knapsack Problem o simplemente KP) es un problema clásico de la Investigación de Operaciones y en particular de la Programación Entera. Consiste en un excursionista que debe preparar su mochila, la cual tiene una capacidad limitada y por tanto no le permite llevar todos los artículos que quisiera tener en la excursión. Cada artículo que el excursionista puede incluir en la mochila le reporta una determinada utilidad. Luego el problema consiste en seleccionar un subconjunto de objetos de forma tal que se maximice la utilidad que el excursionista obtiene, pero sin sobrepasar la capacidad de acarrear objetos.
En este contexto existen varias aplicaciones que guardan una similitud conceptual con el Problema de la Mochila y en consecuencia nos podemos beneficiar de la formulación y resolución de un modelo de optimización matemática para dicho propósito. Consideremos el siguiente ejemplo:
Problema de la Mochila
Un armador tiene un carguero con capacidad de hasta 700 toneladas. El carguero transporta contenedores de diferentes pesos para una determinada ruta. En la ruta actual el carguero puede transportar algunos de los siguientes contenedores:
El analista de la empresa del armador desea determinar el envío (conjunto de contenedores) que maximiza la carga transportada. Para ello se propone el siguiente modelo de Programación Entera:
Variables de Decisión:
Función Objetivo: Consiste en maximizar la carga que transportará el carguero.
Restricciones: El peso de la carga transportada no puede exceder la capacidad máxima del carguero.
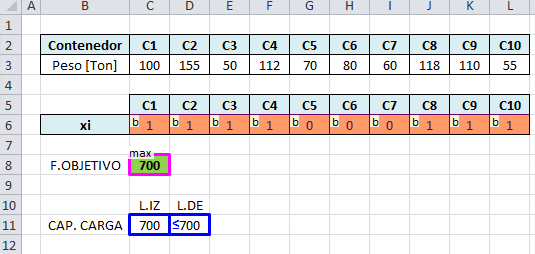
Al implementar computacionalmente el problema anterior haciendo uso de OpenSolver se alcanzan los siguientes resultados:
La solución óptima consiste en transportar los contenedores C1, C2, C3, C4, C8, C9 y C10, con un valor óptimo de 700 (toneladas), es decir, se utiliza la capacidad completa del carguero. Notar que otra solución óptima consiste en transportar los contenedores C1, C3, C4, C5, C6, C7, C8 y C9 lo que reporta un similar valor en la función objetivo.
¿Quieres tener el archivo Excel con la resolución en OpenSolver de este problema?. Recomiéndanos en Facebook o Google+ utilizando la herramienta de redes sociales a continuación y accede de forma gratuita e inmediata a la descarga del archivo.
[sociallocker]Problema Mochila[/sociallocker]
gracias, muy buen aporte
Muy buena explicación! Excelente página. Se entiende muy bien.