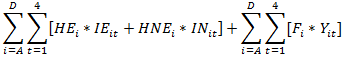El Plan Maestro de la Producción (PMP) especifica las fechas y las cantidades de producción que corresponden a cada uno de los elementos de la familia de productos (manufactura). En muchas aplicaciones el producto no esta terminado en la medida que no haya sido empacado, es decir, que este en una condición de uso suficiente para su comercialización. El siguiente artículo aborda el problema que enfrenta una empresa que debe programar los niveles de producción y empaque para 4 productos en un horizonte de planificación de 8 meses (4 bimestres), buscando satisfacer una demanda estimada al mínimo costo y haciendo uso de recursos limitados.
Planificación de la Producción
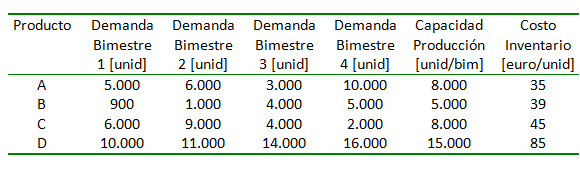
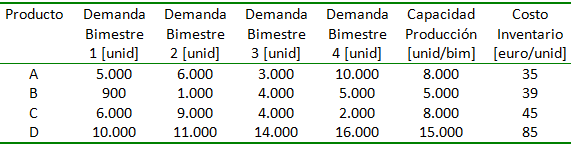
Una firma desea planificar la producción de los próximos 4 bimestres para sus productos finales, representados por los productos A, B, C y D. Esto se hará usando una política óptima de elaboración contra stock para satisfacer las demandas estimadas en cada periodo y cuyos valores se resumen en la siguiente tabla:
En la tabla se entrega igualmente una capacidad máxima de producción por producto, excepto para las labores de empacado. Asuma que estas capacidades son constantes sobre todo el periodo de planificación. En el caso de la sección de empaque esta transforma el producto en un producto empacado, de modo que hay una capacidad global sobre el número total de unidades que pueden ser empacadas en cada periodo y alcanza las 50.000 unidades por bimestre.
Es posible almacenar tanto productos finales como productos finales empacados en una cantidad ilimitada pues la bodega es bastante grande. Sin embargo, hay un costo unitario de mantención de unidades en inventario que se lista en la última columna de la tabla para un producto final empacado y que se asume no cambia en este horizonte de planificación. Asuma que el costo unitario de inventario de un producto final no empacado consiste en restar 4 euros por unidad al valor dado en la tabla para el costo de inventario de uno empacado. El actual inventario es nulo y no hay requerimientos de inventario al final del periodo de planificación.
Cada vez que se emplea la línea de empaque esta debe ser limpiada cuando se planifica empacar cada tipo de producto en un periodo y este proceso de limpieza o esterilización tiene un costo elevado. Dado lo anterior, se espera encontrar una solución donde no necesariamente se empaque de todos los tipos de productos finales en cada periodo. Para representar correctamente esta situación se tomará en cuenta un costo de setup que es independiente del periodo y la cantidad empacada pero si del tipo de producto y está dado por 500.000, 900.000, 800.000 y 900.000 euros para A, B, C y D, respectivamente.
Formule y resuelva computacionalmente un modelo de optimización que permita hallar una política óptima de producción que minimice los costos de inventario y setup, satisfaciendo los requerimientos (estimados) de demanda y las limitaciones en la capacidad de las instalaciones.
Variables de Decisión:
Parámetros: Dada la cantidad de datos del problema propuesto es conveniente trabajar con parámetros, de modo de utilizar una notación más compacta que es equivalente, a saber:
Función Objetivo: Se busca minimizar los costos asociados al proceso de empaque y almacenamiento de productos en inventario (empacados y no empacados) durante el período de planificación. Lo anterior se representa por la siguiente expresión:
Restricciones:
Demanda producto empacado para cada producto i y bimestre t: La demanda de producto empacado de cada uno de los 4 productos en los 4 bimestres se debe satisfacer a través de lo empacado en dicho período y los saldos del mismo (si los hubiere) almacenados en períodos previos.
Balance entre no-empacado y empacados para producto i y bimestre t: De forma similar a las restricciones anteriores, la cantidad de producto a empacar en un período (para cualquiera de las 4 variedades: A, B, B o D) se obtiene como un diferencial entre la producción de producto no empacado más el inventario inicial de producto no empacado menos la cantidad de producto no empacado que se deje en inventario al final del período.
Restricciones Lógicas: La cantidad de producto en un bimestre para un producto en particular no podrá superar las 50.000 unidades en caso que se decida empacar dicho producto en aquel período, en caso contrario no se empaca.
Capacidad de empacado para cada bimestre t: La cantidad de productos A, B, C o D que en total se empaquen en cada período no puede superar la capacidad de empaque de 50.000 unidades por período.
Capacidad de producción en cada familia y bimestre t: Se debe respetar la capacidad de producción de producto no empacado para cada variedad y en cada período del horizonte de planificación.
No negatividad: Las variables de decisión deben adoptar valores no negativos.
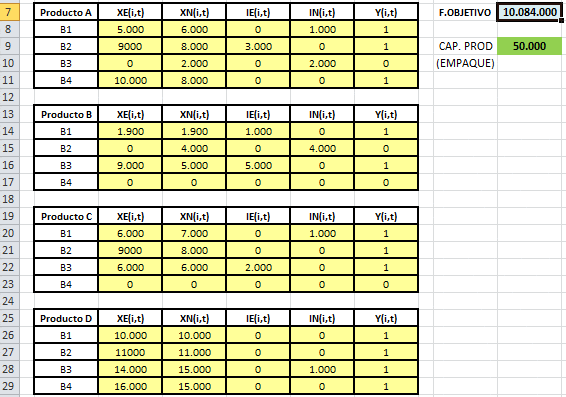
La siguiente imagen muestra la solución óptima (celdas amarillas) y valor óptimo (celda celeste) alcanzado a implementar este modelo de Programación Entera Mixta haciendo uso de Premium Solver Pro.
Consideremos el producto A de modo de ejemplificar respecto a la interpretación de los resultados. Se producen 6.000 unidades del producto A y se empacan sólo 5.000 de ellas en el bimestre 1 (con las que se satisface la demanda del bimestre 1), en consecuencia, al final del período se dispone de 1.000 unidades de producto A no empacado. Notar adicionalmente que a excepción del producto D para el resto de los productos no se empaca en todos los períodos.
¿Quieres tener el archivo Excel con la resolución en Premium Solver Pro de este problema?.
[sociallocker]solver-produccion-y-empaque[/sociallocker]