Cuando necesitamos asignar recursos escasos a determinadas funciones y dichos recursos no son fraccionables, la utilización de modelos de Programación Entera resultan ser de utilidad para la toma de decisiones. En este contexto los problemas de asignación de personal a determinadas tareas es una aplicación típica de la Programación Entera que a continuación desarrollaremos a través de un ejemplo.
Problema de Asignación
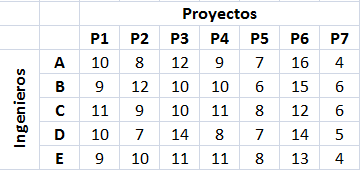
Consideremos una empresa que dispone de 5 ingenieros que deben desarrollar 7 proyectos. La tabla a continuación resume el tiempo que demora cada ingeniero (en horas) en completar un determinado proyecto. El problema consiste en determinar una asignación óptima que permita realizar cada uno de los proyectos con la limitante que por motivos estratégicos cada ingeniero debe desarrollar al menos un proyecto y en ningún caso hacer más de 2 proyectos. Por supuesto se busca que el tiempo requerido para realizar los 7 proyectos sea el menor posible.
Una alternativa sería buscar intuitivamente una asignación que cumpla con los requisitos de la empresa y tenga un bajo tiempo asociado. Sin embargo, este tipo de estrategias de resolución queda claramente acotada a problemas de tamaño menor y ni siquiera en ese tipo de situaciones nos asegura la mejor solución posible. Por ello definiremos el siguiente modelo de optimización de Programación Entera:
1. Variables de Decisión: Utilizamos las siguientes variables de decisión binarias
2. Función Objetivo: Minimizar el tiempo total requerido para completar los proyectos
Donde Tij (parámetros) es el tiempo (en horas) requerido por el ingeniero i en realizar el proyecto j. Por ejemplo T(A,P5)=7.
3. Restricciones:
Cada proyecto debe ser realizado por un solo ingeniero:
Cada ingeniero debe ser al menos un proyecto y no puede hacer más de 2:
El siguiente tutorial muestra cómo resolver este problema de asignación con Solver de Excel:
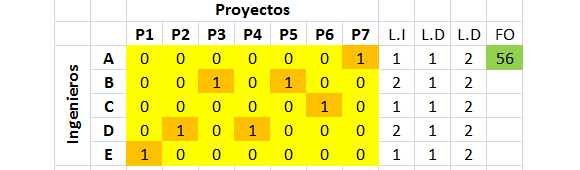
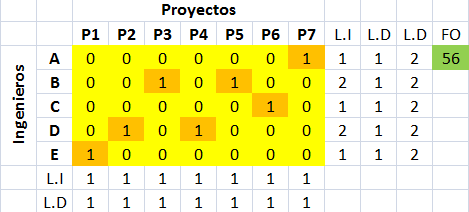
Se puede observar que para efectos de Solver, las variables de decisión binarias se deben definir como una restricción adicional. También puede resultar que luego de resolver Solver no encuentre inmediatamente la mejor solución posible. Para enfrentar esta situación se puede «volver a resolver» sobre la solución que el programa nos haya proporcionado hasta el momento para verificar si se puede lograr algo mejor. Esta situación es la que sucedió en el tutorial y a continuación se muestra la solución óptima (final) encontrada por Solver.
En total se requieren 56 horas para realizar los 7 proyectos. El ingeniero A realiza el P7, el ingeniero B el P3 y P5, el ingeniero C el P6, el ingeniero D el P2 y P4 y el ingeniero E el P1. Notar que cada proyecto es realizado por un ingeniero y cada ingeniero al menos realiza un proyecto, pero no más de 2 proyectos.
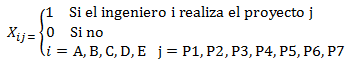
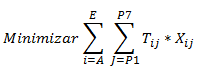
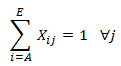
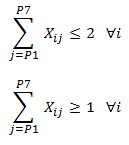
hola como deduces que cada ingeniero no puede hacer mas de 2 proyectos?
o quizá esas ya eran las restricciones de tus problemas 😕
@lucia. Es un supuesto que hemos asumido para la formulación del modelo. Es parte de la descripción del problema.
¿Qué significa las iniciales L.I y L.D?. Gracias
@Annie. Es sólo una abreviación, L.I representa el lado izquierdo de las restricciones y L.D. el lado derecho de las restricciones.
¿Qué pasaría si agrego que el proyecto 5 no lo puede realizar el ingeniero B?, ¿cómo cambiaría la restricción?
@Luis. Si el ingeniero B no puede realizar el proyecto 5 se puede imponer como restricción adicional X(B,P5)=0.
¿Cómo dedujiste que la función objetivo de este problema quedaría en minimizar z?
@Diego. Simplemente en base a la información detallada en la problemática donde naturalmente se busca completar los proyectos en el menor tiempo posible.
Hola. ¿Cómo podrías asignar prioridades a cada proyecto?
@Javier. En la formulación propuesta se deben desarrollar todos los proyectos. No obstante no siempre se dispone de los recursos necesarios para abordar la totalidad de proyectos que puedan estar en cartera. En este contexto se puede «penalizar» en la función objetivo el no considerar un proyecto al momento de tomar una decisión y esa penalización puede ser diferenciada entre proyectos de modo de asignar una importancia relativa.
Hola, ¿hay alguna posibilidad de que con el Solver (u otro programa si conoces) se muestren todas las soluciones óptimas posibles? Porque a mí me da FO=56 como a ti, pero las asignaciones óptimas me han salido diferente: Ingeniero A el P7, el B el P5, el C los P3 y P6, el D los P2 y P4 y el E el P1.
Gracias!
@Ana. En términos prácticos lo relevante es encontrar una solución óptima y con ello tienes garantía de que no existe alguna solución factible que estés omitiendo que tenga mejor valor en la función objetivo. No es necesario enumerar «todas» las soluciones óptimas (por ejemplo, en Programación Lineal se puede dar el caso de tener infinitas soluciones óptimas).
¿Qué significa la A al revés?