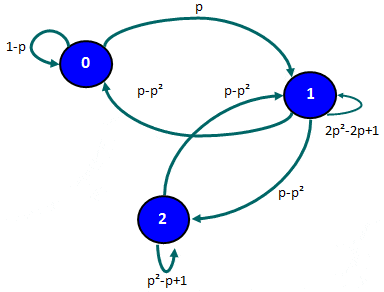
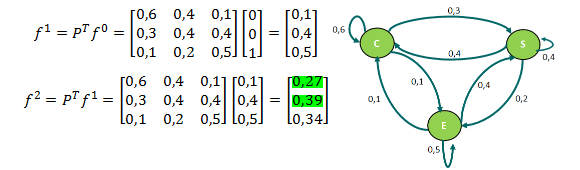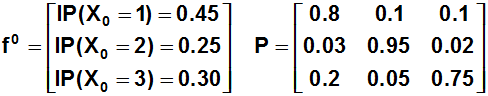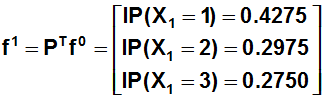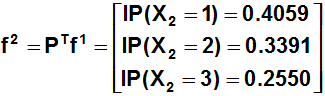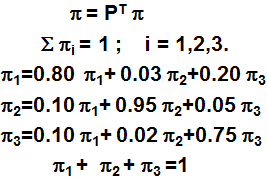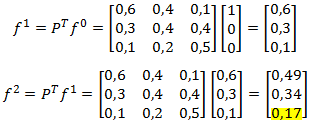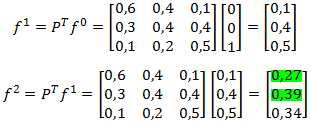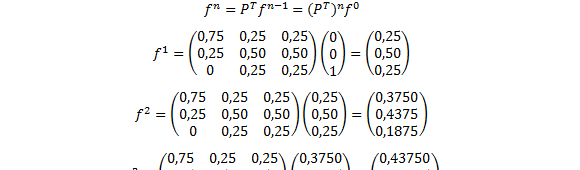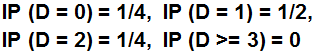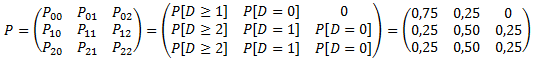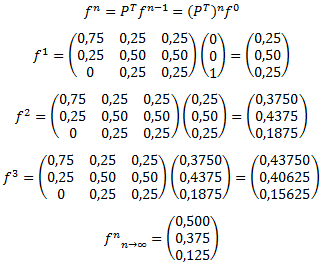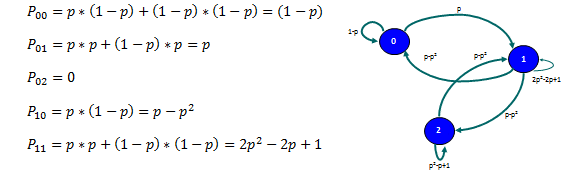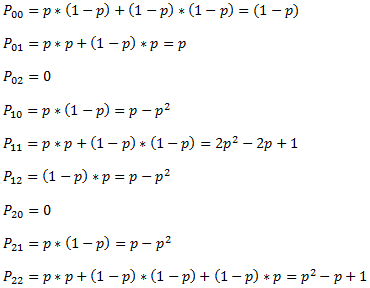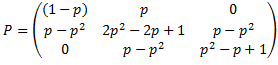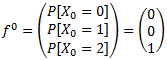variable aleatoria Archivos - Gestión de Operaciones

Cadenas de Markov (Ejercicios Resueltos)

Un proceso estocástico en tiempo discreto se denomina una Cadena de Markov en tiempo discreto si y solo sí se satisface la Propiedad Markoviana (esto es básicamente que el futuro t=n+1 es independiente del pasado dado el presente t=n) y Propiedad Estacionaria (la probabilidad de pasar de un estado i a un estado j al cabo de una etapa no depende de la etapa n). A continuación presentamos un conjunto de problemas resueltos de Cadenas de Markov que sirvan de complemento para los estudios de nuestros usuarios.

Ejercicios Resueltos de Cadenas de Markov

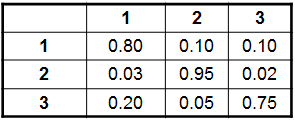
Ejercicio N°1: Una empresa esta considerando utilizar Cadenas de Markov para analizar los cambios en las preferencias de los usuarios por tres marcas distintas de un determinado producto. El estudio ha arrojado la siguiente estimación de la matriz de probabilidades de cambiarse de una marca a otra cada mes:

Si en la actualidad la participación de mercado es de 45%, 25% y 30%, respectivamente. ¿Cuales serán las participaciones de mercado de cada marca en dos meses más?.

En primer lugar definimos la variable aleatoria $X_{n}$ que representa la marca que adquiere un cliente cualquiera en el mes n. Dicha variable aleatoria puede adoptar los valores 1,2,3 en el mes n=0,1,2,3,..

Adicionalmente conocemos cuál es la distribución inicial y la matriz de probabilidades de transición en una etapa tal como se observa a continuación:

Luego para conocer la distribución de las participaciones de mercado al cabo de 2 meses (2 etapas) podemos utilizar la fórmula $f^{n}=P^{T}*f^{n-1}$ :

Se concluye que las cuotas de mercado (participaciones de mercado) en dos meses a cambiado de un 45% a un 40.59%; de un 25% a un 33.91% y de un 30% a un 25.50%, para las marcas 1,2 y 3 respectivamente.

Ejercicio N°2: ¿Cuál es la cuota de mercado en el largo plazo para cada una de las marcas descritas en el Ejercicio N°1?.

La Cadena de Markov del Ejercicio N°1 es irreducible (es decir todos los estados se comunican entre sí) con estados recurrentes positivos y aperiódicos. Lo anterior se concluye luego de la Clasificación de Estados de una Cadena de Markov en Tiempo Discreto. Verificado lo anterior podemos obtener la Distribución Límite de una Cadena de Markov en Tiempo Discreto a través del siguiente sistema de ecuaciones:

La solución del sistema corresponde a: $\pi _{1}=0,2373$ , $\pi _{2}=0,6184$ y $\pi _{3}=0,1443$ , que representan las cuotas de mercado en el largo plazo para las marcas 1,2 y 3, respectivamente. Notar que las actuales participaciones de mercado difieren significativamente de las cuotas obtenidas en el largo plazo lo cual sugiere que de alguna manera deban ser corregidas las probabilidades de transición.

Ejercicio N°3: En una Unidad de Cuidados Intensivos en un determinado hospital, cada paciente es clasificado de acuerdo a un estado crítico, serio o estable. Estas clasificaciones son actualizadas cada mañana por un médico internista, de acuerdo a la evaluación experimentada por el paciente. Las probabilidades con las cuales cada paciente se mueve de un estado a otro se resumen en la tabla que sigue:

¿Cuál es la probabilidad que un paciente en estado crítico un día Jueves esté estable el día Sábado?.

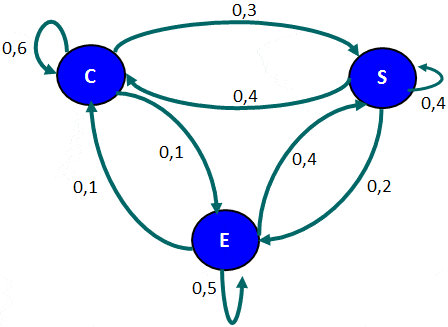
Sea $X_{n}$ la variable aleatoria que indica el estado que se encuentra un paciente cualquiera en el hospital en el día n. Los valores posibles para dicha variable son C, S y E, representando los estados crítico, serio y estable, respectivamente. Un grafo que representa dicho proceso estocástico dada la tabla anterior es:

La probabilidad de que un paciente esté en estado crítico el día Jueves y que el día Sábado esté estable, esta dado por: $\mathbb{P}_{CE}^{2}$ , es decir, la probabilidad de pasar del estado crítico al estado estable al cabo de 2 etapas (días).

$\mathbb{P}_{CE}^{2}=0,3*0,2+0,1*0,5+0,6*0,1=0,17$

Notar que de forma equivalente se pueden utilizar las ecuaciones matriciales $f^{n}=P^{T}*f^{n-1}$ :

Se comprueba que la probabilidad de pasar del estado crítico al estado estable al cabo de 2 etapas es de un 17%.

¿Cuál es la probabilidad que un paciente que está en estado estable el Lunes experimente alguna complicación y no esté estable nuevamente el Miércoles?.

En este caso cambia la distribución inicial respecto al escenario anterior (ahora el paciente está en estado estable), no obstante, también resulta de nuestro interés analizar qué sucede al cabo de 2 etapas.

Con color verde se marca la probabilidad de que comenzando en un estado estable al cabo de 2 días un paciente se encuentre en estado crítico o serio. La suma de dichas probabilidades es un 66% que da respuesta a la interrogante anterior.

¿Qué porcentaje de la Unidad de Cuidados Intensivos usted diseñaría y equiparía para pacientes en estado crítico?.

Naturalmente se desea estimar la probabilidades de estado en el largo plazo independiente de la distribución inicial. La cadena es irreducible con estados recurrentes positivos aperiódicos. Utilizando las ecuaciones de estado estable presentadas en el Ejercicio N°2 se obtiene que $\pi _{C}\cong0,2373$ , $\pi _{S}\cong0,6184$ y $\pi _{E}\cong0,1443$ , que representan la probabilidad de que un individuo se encuentre en estado crítico, serio y estable, respectivamente.

El software Interactive Operations Research Tutorial (IORTutorial) permite estimar las probabilidades de largo plazo luego de ingresar la matriz de probabilidades de transición según se muestra a continuación:

Comentarios: En el Blog hemos desarrollado otros ejercicios resueltos que recomendamos revisar, entre ellos uno que aborda una Política de Gestión de Inventarios a través de Cadenas de Markov en Tiempo Discreto y Ejemplo de una Cadena de Markov en Tiempo Discreto. Adicionalmente en la categoría de contenidos de Cadenas de Markov periódicamente estamos publicando nuevo material didáctico sobre dicha materia. Esperamos que este material sea de utilidad para tus estudios y te agradecemos puedas ayudarnos a difundir éste a través de las redes sociales.

Gestión de Inventarios a través de Cadenas de Markov en Tiempo Discreto

La gestión de inventarios hace uso de distintas herramientas metodológicas que abordan 2 preguntas básicas: ¿de qué tamaño debe ser un pedido? y ¿cada cuánto tiempo se debe realizar un pedido?. En el siguiente artículo se propone la utilización de una Cadena de Markov en tiempo discreto para determinar la política de reposición de inventarios de una empresa: Una tienda que mantiene un inventario de un producto dado para satisfacer una demanda (aleatoria). La demanda diaria D, tiene la siguiente distribución de probabilidades:

Consideremos una política de inventarios denominada (q,Q), que indica que si el nivel de inventarios al final de cada día es menor a q=2 se ordenan Q=1 unidades adicionales (las cuales se asumen disponibles al inicio del día siguiente), en caso contrario no se hace ninguna orden. La demanda no satisfecha es venta perdida y hay 2 unidades al final en n=0 (distribución inicial). Sea Xn el nivel de inventario al final del día n (esto corresponde a la definición de la variable aleatoria), interesa modelar el problema mediante una Cadena de Markov.

Un primer desafío consiste en determinar los posibles estados que puede adoptar la variable aleatoria en una etapa n cualquiera. Notar que es posible finalizar un día sin unidades en inventario, dado que si bien esta situación genera una reposición de 1 unidad, ésta se asume disponible al inicio del día siguiente. Adicionalmente también es posible terminar un día con 1 o 2 unidades en inventario (en estos casos no se genera reposición). Sin embargo, no es posible terminar un día con 3 unidades en inventario (recordar que en n=0 se dispone de 2 unidades en inventario y dada la política de reposición, ésta se genera cuando se dispone de menos de 2 unidades en inventario). En resumen, los estados posibles para la variable aleatoria son Xn℮{0,1,2}.

A continuación estimamos las probabilidades de transición en una etapa las cuales se resumen en la siguiente matriz de probabilidades de transición (matriz P):

Por ejemplo, si en un día n en particular se finaliza con 0 unidades en inventarios se genera un pedido que al inicio del día siguiente permitirá disponer de 1 unidad; para que dicho día (n+1) se termine con 0 unidades en inventario se requiere que la demanda sea mayor o igual a 1 unidad (este es el caso de P00).

Adicionalmente se pueden estimar las probabilidades estacionarias, es decir, que en el largo plazo (independiente de la distribución inicial) se disponga al final de un día de 0, 1 o 2 unidades en inventario. Para ello se debe clasificar los estados de la cadena donde en particular se corrobora que ésta es irreducible con estados recurrentes positivos aperiódicos.

En consecuencia la probabilidad de que en el largo plazo se disponga de 0 unidades al final de un día es de un 50% (1/2), tener una unidad es un 37,5% (3/8) y 2 unidades un 12,5% (1/8). Alternativamente podemos hacer uso de las ecuaciones matriciales para que partiendo de la distribución inicial (dato) se estime la probabilidad de encontrarse en cualquiera de los estados al cabo de 1, 2, …, n etapas (con n que tiende a infinito). Dicho resultado corrobora los resultados anteriores:

Se propone al lector comprobar que independiente de la selección de la distribución inicial las probabilidades de largo plazo son las expuestas.

Ejemplo de una Cadena de Markov en Tiempo Discreto

En el siguiente artículo abordaremos la formulación de una Cadena de Markov en tiempo discreto, para la cual identificaremos la variable aleatoria que resulta de interés su análisis, los posibles estados que puede adoptar dicha variable en un periodo cualquiera y las probabilidades de transición en una etapa que se puede resumir en una matriz de transición de probabilidades conocida como matriz P. En dicho contexto consideremos el siguiente ejemplo:

Un individuo posee 2 paraguas los cuales emplea para ir de su casa al trabajo y viceversa (llevando uno a la vez). Si está en casa (oficina) al comienzo (final) del día y está lloviendo toma un paraguas, si lo hay para ir de su casa a la oficina y viceversa. Asuma que independiente del pasado llueve al comienzo (final) del día con probabilidad p (0<p<1). Se desea modelar el número de paraguas en su casa al inicio del día n, suponiendo que inicialmente ambos paraguas están en su casa.

El problema sugiere como variable aleatoria el modelamiento del número de paraguas que tiene el individuo en su casa al inicio del día n:

Los posibles estados o valores que puede adoptar la variable aleatoria en una etapa n cualquiera son 0, 1 o 2. Es decir, el individuo podrá tener en su casa al inicio de un día en particular 0, 1 o 2 paraguas.

A continuación corresponde identificar las probabilidades de transición en una etapa, lo cual depende de la dinámica de la situación planteada:

Por ejemplo P(0,0) representa la probabilidad de que un día el individuo no tenga paraguas en su casa (por tanto los 2 paraguas están en la oficina) y que al inicio del día siguiente siga en la misma situación (es decir, sin paraguas en la casa). Los escenarios que permiten esta situación son que llueva en la mañana (con probabilidad p) y que no llueva en la tarde (con probabilidad 1-p). Adicionalmente si no llueve en la mañana (con probabilidad 1-p) y no llueve en la tarde (con probabilidad 1-p) el individuo al inicio del día siguiente no tendrá paraguas en la casa. En consecuencia se puede notar que para este caso lo relevante es que no llueva en la tarde (sin importar si llueve o no en la mañana) para que de esta forma el individuo no se lleve un paragua desde la oficina a la casa.

Otra combinación interesante es P(2,2) que considera la probabilidad de tener los 2 paraguas en la casa al inicio de un día (y por tanto ninguno en la oficina) y al inicio del día siguiente también tener 2 paraguas en la casa. Para ello se debe cumplir alguno de los siguientes escenarios: que llueva en la mañana y en la tarde, que no llueva ni en la mañana ni en la tarde o que no llueva en la mañana pero si llueva en la tarde.

Una vez identificadas todas las probabilidades de transición en una etapa entre estados, éstas se pueden resumen en la matriz de probabilidades de transición (conocida también como matriz P). Notar que la suma de las probabilidades de cada una de las filas de la matriz es (y debe ser) un 100%.

Alternativamente la información anterior se puede representar a través de un grafo donde cada nodo representa un estado y las flechas muestran si es posible pasar de un estado a otro al cabo de una etapa (y cuál es la probabilidad asociada en dicho caso):

Adicionalmente se puede identificar (si se cuenta con dicha información) la distribución inicial de estados que permite identificar cuál es la probabilidad que al inicio de la planificación el proceso se encuentre en alguno de los n estados posibles. En este ejemplo sabemos que se comienza con 2 paraguas en la casa:

Con la información recabada en este problema estamos en condiciones de poder estimar cuál es la probabilidad que comenzando en un estado i pasemos a un estado j al cabo de n etapas (pasos). Este tipo de análisis y otros complementarios los abordaremos en un próximo artículo.

Actualización: Se recomienda consultar el artículo Cadenas de Markov (Ejercicios Resueltos) para encontrar material de estudio complementario al presentado en esta publicación.