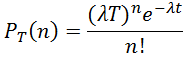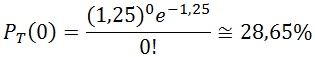probabilidad Archivos - Gestión de Operaciones

Cálculo de la Probabilidad de un Número de Llegadas en un Tiempo Determinado utilizando la Distribución de Poisson

Cuando los clientes llegan a un servicio de forma totalmente aleatoria (es decir, no hay forma de pronosticar cuándo va a llegar alguien) la función de densidad de probabilidad para describir la cantidad de llegadas durante un tiempo determinado se representa por la Distribución de Poisson y automáticamente la distribución del tiempo entre llegadas sigue una Distribución Exponencial según lo expuesto en el artículo Propiedad de Falta de Memoria o Amnesia de la Distribución Exponencial.

En este contexto la fórmula que permite calcular la probabilidad exacta de $n$ llegadas dentro de un período $T$ es la siguiente:

Consideremos por ejemplo un taller que se dedica a labores de reparación y que la llegada de éstos diariamente se comporta de forma aleatoria con una tasa de 10 trabajos diarios. ¿Cuál es la probabilidad de que no lleguen trabajos durante una hora cualquiera bajo el supuesto que el taller opera 8 horas al día?.

Notar que $\lambda =\frac{10}{8}=1,25[\frac{trabajos}{hora}]$ . Es decir, la probabilidad de no recibir trabajos durante una hora cualquiera es aproximadamente a un 28,65%.

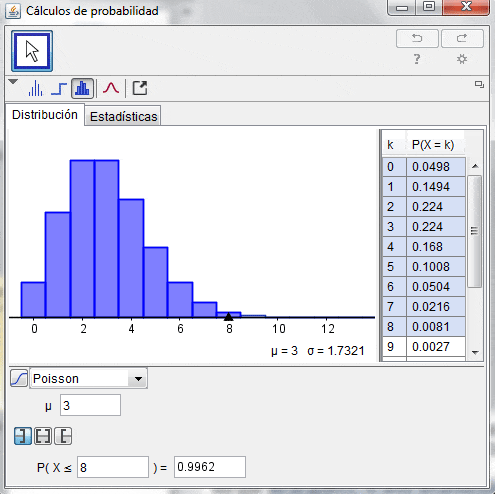
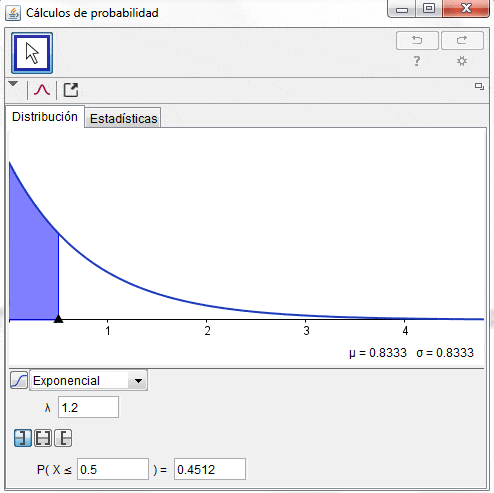
Asumamos ahora una nueva situación. Un proceso que tiene una tasa promedio de llegada de 6 clientes por hora ( $\lambda =6[clientes/hora]$ ) y se desea evaluar cuál es la probabilidad de que lleguen exactamente 0, 1, 2,…,n clientes en un intervalo de tiempo de 0,5 horas (30 minutos). El siguiente vídeo proporciona una simulación de dicho escenario:

En el gráfico, el área amarilla, por ejemplo, significa exactamente la probabilidad que 3 personas lleguen en las 0,5 horas. El área amarilla más el área roja, por ejemplo, significa la probabilidad de que lleguen 2 o 3 personas en los 30 minutos.

Adicionalmente haciendo uso del software Geogebra y su herramienta cálculos de probabilidad, se puede representar la Distribución de Poisson para los parámetros descritos anteriormente de forma de obtener rápidamente los resultados para distintos números de llegadas (notar que la Distribución de Poisson es discreta).

Propiedad de Falta de Memoria o Amnesia de la Distribución Exponencial

En el análisis del comportamiento de las Líneas de Espera, se reconoce que el proceso de llegada de los clientes al sistema ocurre de forma totalmente aleatoria. Se entiende por aleatorio que la ocurrencia de un evento no se ve afectado por el tiempo transcurrido desde la ocurrencia de un evento anterior. Por ejemplo, si en estos momentos son las 10:30 y la última llegada de un cliente fue a las 10:15, la probabilidad de que la siguiente llegada sea a las 10:35 es función sólo de las 10:30 a las 10:35 y en consecuencia es totalmente independiente del tiempo transcurrido desde la ocurrencia del último evento, es decir, de las 10:15 a las 10:30. Este resultado se conoce como falta de memoria o amnesia de la Distribución Exponencial.

Consideremos el siguiente ejemplo que permite ilustrar esta situación: Una máquina en operación tiene una unidad de reserva para sustituirla de inmediato cuando falla. El tiempo medio entre fallas (conocido también como MTBF o Mean Time Between Failures) se distribuye exponencial y sucede cada 50 minutos (en promedio). El operario de la máquina comenta que ésta suele descomponerse cada tarde a eso de las 17:00. Se requiere analizar la validez de lo que señala el operario.

El tasa promedio de fallas de la máquina es $\lambda =60/50=1,2[fallas/hora]$ . Luego la distribución exponencial del tiempo entre fallas se representa por $f(t)=1,2e^{-1,2t}, t>0$ .

Se concluye que lo que señala el operario no es correcto dado que contradice a que el tiempo entre fallas se distribuye exponencial y que por consiguiente es totalmente aleatorio. Dicho de otro modo la probabilidad de que la máquina falle a las 17:00 dependerá de la hora del día (en relación a las 17:00) con la que se calcule. Por ejemplo, si ahora son las 16:30, la probabilidad de que lo que afirma el operador sea cierto es:

El resultado anterior se puede corroborar haciendo uso de la herramienta de cálculos de probabilidad del software Geogebra:

A continuación presentamos un breve tutorial de nuestro canal de Youtube con la implementación en Geogebra del ejemplo anterior:

Cálculo de los Beneficios Esperados de un Proyecto utilizando PERT

Un aspecto usual en la Gestión de Proyectos es enfrentar incentivos económicos por entregas anticipadas o a tiempo en base a la planificación preliminar y adicionalmente multas o cargos por entregas atrasadas o tardías. En este contexto el método PERT (Program Evaluation and Review Technique) permite incorporar de forma explícita la incertidumbre asociada a los tiempos requeridos para completar cada una de las actividades de un proyecto.

Beneficios Esperados de un Proyecto utilizando PERT

En el siguiente ejemplo se presenta la situación de un proyecto que consta de 9 actividades, cuyas relaciones de precedencia y tiempos en días (pesimista, más probable y optimista) se resumen a continuación:

Donde $N\sim (\mu ,\sigma ^{2})$ y los tiempos están en días.

Se desea completar el proyecto al cabo de 40 días a contar del inicio de las actividades. En caso de terminar antes de dicho plazo se estima que se accederá a un incentivo monetario de $200.000, no obstante, en caso contrario se asumirá una pérdida de $15.000 por cada día de atraso con un tope máximo de $30.000 (sobre los beneficios estimados). ¿Cuál es la ruta crítica del proyecto?, ¿Cuáles son los beneficios esperados del proyecto?.

Sabemos que el tiempo esperado para cada actividad se obtiene de $Te=\frac{(a+4m+b)}{6}$ , por ejemplo, $Te_{A}=\frac{(6+4*7+8)}{6}=7$ . Adicionalmente la varianza se obtiene de $\sigma ^{2}=\frac{(b-a)^{2}}{36}$ , por ejemplo, $\sigma ^{2}_{A}=\frac{(8-6)^{2}}{36}=\frac{1}{9}\cong 0,111$ . Con la ayuda de Excel resulta sencillo replicar el procedimiento para el resto de las actividades como se muestra a continuación:

Considerando el Tiempo Esperado (Te) para cada una de las actividades generamos un diagrama de proyecto que nos permita identificar la Ruta Crítica y las holguras (en días) para cada una de las actividades. De esta forma se obtiene que A-D-F-H es la ruta crítica del proyecto con un tiempo esperado para completar éste de 39 días.

Donde los valores con color rojo en la esquina superior izquierda de cada nodo representan el inicio más cercano; los valores con color azul de la esquina superior derecha el término más cercano; los valores de la esquina inferior izquierda con color naranjo el inicio más lejano y finalmente los números con color verde en la esquina inferior derecha representan el término más lejano.

A continuación se requiere estimar la probabilidad de completar el proyecto antes de 40 días, caso en el cual se accede a un beneficio de $200.000.

$\mathbb{P}[T<40]=\mathbb{P}[Z_{\alpha }<\frac{40-39}{\sum {\sigma _{RC}}^{2}}]=\frac{40-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,6544$

El beneficio esperado en este escenario sería $200.000*0,6544=$130.880.

Por otra parte la probabilidad de que el proyecto demore más de 41 días se obtiene de la siguiente forma:

$\mathbb{P}[T>41]=\mathbb{P}[1-Z_{\alpha }<\frac{41-39}{\sum {\sigma _{RC}}^{2}}]=\frac{41-39}{\sqrt{(\frac{1}{9})+(\frac{4}{9})+(\frac{16}{9})+4}}\cong0,2134$

Con un beneficio esperado de $170.000*0,2134=$36.278.

Finalmente evaluamos el caso donde el tiempo del proyecto se encuentra en el intervalo entre 40 y 41 días.

$\mathbb{P}[T\geq40]+\mathbb{P}[T\leq 41]=0,1322$

Siendo el beneficio esperado de este escenario $185.000*0,1322=$24.457.

En consecuencia el beneficio esperado asociado a completar el proyecto es de $191.615 ($130.880+$36.278+$24.457).

Cómo calcular la Probabilidad de producir un Producto Defectuoso (Control Estadístico de Procesos)

El siguiente artículo aborda a través de un sencillo ejemplo la estimación de la probabilidad de producir un producto defectuoso en el contexto del Control Estadístico de Procesos (CEP). Consideremos una empresa de manufactura que desea determinar si una máquina que tiene es capaz de fresar la pieza de un motor que tiene una especificación clave de 4 ± 0.003 pulgadas. Después de probar esta máquina, la empresa determinó que tiene una media muestral de 4.001 pulgadas con una desviación estándar de 0.002 pulgadas. Asumiendo que el proceso en cuestión se encuentra bajo control estadístico, calcule Cpk para esta máquina:

¿Cuál es la probabilidad de producir un defecto?. Un producto defectuoso será aquel que se encuentre en una dimensión bajo el LEI (3,997) o sobre el LES (4,003).

Probabilidad de Defectuoso = P(X<LEI) + P(X>LES) = (1 – 0,9773) + (1 – 0,8413) = 18,14%.

Una forma alternativa de abordar el procedimiento anterior es haciendo uso de la interfaz de cálculos de probabilidad disponible en el software Geogebra. En la siguiente imagen el área achurada en color azul representa la probabilidad de que un producto no sea defectuoso (81,86%), por tanto por diferencia se obtiene la probabilidad de defectuoso (100% – 81,86% = 18,14%) que corrobora el resultado obtenido anteriormente.

¿Recomendaría a la empresa utilizar esta máquina para producir esta pieza?. No. Cpk indica que el promedio muestral está descentrado, en particular, más cerca del LES. Si bien es difícil encontrar un proceso perfectamente centrado en el valor nominal de la especificación, en este caso esta situación no se compensa con una baja variabilidad del proceso (se propone al lector corroborar que Cp=0,5 lo cual confirma el análisis anterior). Adicionalmente la probabilidad de producir un defecto (18,14%) es inadmisible es un contexto competitivo.

Cómo ajustar una Función de Probabilidad Teórica a una serie de datos Empíricos

En el análisis del comportamiento de una línea de espera se suele considerar la premisa de que el tiempo entre llegada de los clientes se distribuye exponencial con parámetro lambda (λ). Si bien esta presunción es válida en muchas situaciones es conveniente realizar un diagnóstico de dicha situación a través de test estadísticos ad hoc. En este contexto el siguiente artículo aborda el problema de ajuste de una función de probabilidad teórica a una serie de datos empíricos que como se menciono anteriormente es un asunto de interés en el análisis de los sistemas de espera como así también en un sin número de aplicaciones estadísticas clásicas.

La data que utilizaremos en este tutorial fue obtenida del Libro Matching Supply with Demand: An Introduction to Operations Management. Esta corresponde a las 686 llamadas que ha recibido un Call Center en un período de 4 horas según se muestra a continuación:

La pregunta que queremos responder es: ¿El tiempo entre llamada de los clientes se distribuye exponencial?. Análogamente ¿Qué función de probabilidad teórica ajusta de mejor forma los datos empíricos?. Para enfrentar dichas interrogantes utilizaremos el software Easyfit que hemos abordado en artículos anteriores para la confección de histogramas y análisis de estadísticas descriptivas.

Preliminarmente ordenaremos los datos recolectados en una columna y procedemos a calcular el tiempo transcurrido entre cada llamada (Iai), por ejemplo, entre la primera y segunda llamada pasan 23 segundos, entre la segunda y tercera llamada pasan 1 minuto y 24 segundos (equivalente a 84 segundos) y así sucesivamente. A continuación se muestra un extracto de dicho procedimiento:

Con los tiempos entre llamadas en segundos (o su equivalencia en minutos si así se desea) se hace uso de Easyfit. Copiamos dichos tiempos en la columna A tal se muestra en la siguiente imagen y luego la opción «Ajustar distribuciones»:

Luego seleccionamos «OK»:

El programa se ejecuta y proporciona los resultados de los ajustes de los datos empíricos a un importante número de distribuciones teóricas, proporcionando una estimación de los parámetros respectivos.

La distribución Wakeby es la que muestra el mejor ajuste, considerando los siguientes parámetros:

Adicionalmente podemos obtener los test de bondad de ajuste (en la pestaña «Bondad de ajuste»). Probablemente el más conocido de ellos es el test Chi-cuadrado (notar que las distribuciones han sido ordenadas en base a este criterio). También se puede obtener el detalle de las pruebas de hipótesis para distintos niveles de significancia estadística (valores de alfa).

Una interpretación exhaustiva de los test de bondad de ajuste requiere de una discusión más detallada que escapa a los propósitos de este artículo. No obstante queda de manifiesto que existen herramientas computacionales que permite simplificar este tipo de análisis que es recurrente en el ámbito de la estadística y por cierto en el de la gestión de operaciones.