El Método Simplex Dual nos ofrece una alternativa algorítmica para abordar la resolución de modelos de Programación Lineal. En particular este método se puede utilizar cuando luego de llevar a la forma estándar un modelo de Programación Lineal no se dispone de una solución básica factible inicial con la cual se pueda dar inicio a las iteraciones del algoritmo. En este contexto a continuación se presenta un ejemplo con los detalles de la aplicación de este procedimiento.
Ejemplo del Método Simplex Dual
Consideremos el siguiente problema para ilustrar sobre la aplicación del Método Simplex Dual:
Para llevar el problema anterior a la forma estándar se requiere agregar 2 variables de exceso no negativas para la restricción 1 y 2, que llamaremos respectivamente X4 y X5. De esta forma el problema en su formato estándar queda definido por:
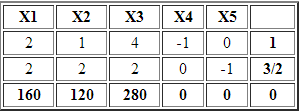
Luego construimos la tabla inicial del Método Simplex:
¿Cómo continuar con las iteraciones del Método Simplex?. Antes de ello es necesario disponer de una solución básica factible inicial. En este contexto si quisiéramos usar X4 y X5 como variables básicas (y en consecuencia X1, X2 y X3 como variables no básicas) se requiere que X4 y X5 sean mayores o iguales a cero, sin embargo, sus coeficientes en las respectivas filas son negativos y por tanto no se dispone de la identidad (matriz con «1» como diagonal y el resto de coeficientes igual a cero).
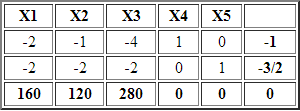
En consecuencia para formar la identidad podemos multiplicar por «-1» la fila 1 y 2, obteniendo lo siguiente:
En la tabla anterior se tiene una solución básica (infactible en las variables primales), pero al tener costos reducidos no negativos esto define una solución básica factible en el dual.
Ahora X4 y X5 son variables básicas y adoptan los valores de -1 y -3/2, respectivamente, lo que claramente no satisface las condiciones de no negatividad para las variables de decisión, es decir, no corresponde a una solución básica factible.
Sin embargo, en esta instancia podemos aplicar el Método Simplex Dual como alternativa de resolución. Para ello seleccionaremos una variable que deje la base y adoptaremos como criterio de selección aquella variable básica asociada al lado derecho «más negativo» (con esto se busca favorecer la rapidez de convergencia).
En el ejemplo dicha variable es X5. Luego para determinar que variable entra a la base realizamos un mínimo cuociente entre el negativo del costo reducido de las variables no básicas y las entradas estrictamente menores a cero para las variables no básicas en la fila 2 (fila asociada al lado derecho más negativo).
Es decir: Min{-160/-2; -120/-2; -280/-2}=60 ==> el cuociente mínimo se alcanza en la segunda columna asociada a la variable no básica X2, por tanto dicha variable entra a la base.
En cada iteración del Método Simplex Dual se escoge un lado derecho con valor negativo, identificando la respectiva variable básica primal, quien deja la base.
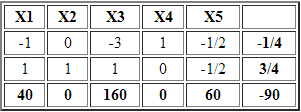
Finalmente se realiza una iteración realizando las operaciones filas que sean necesarias, de modo de ingresar X2 a la base al mismo tiempo que X5 deja la base. Los resultados serían:
Notar que ahora las variables básicas son X4 y X2 donde sólo X4=-1/4 lo que no satisface la condición de ser una solución básica factible. Por lo tanto realizamos una nueva iteración, en este caso sacando de la base a la variable X4 y calculamos el mínimo cuociente: Min{-40/-1; -160/-3; -60/-1/2}=40 ==> el cuociente mínimo está en la primera columna por tanto la variable X1 entra a la base.
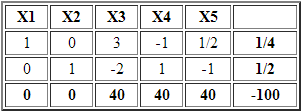
En consecuencia se actualiza la tabla quedando lo siguiente:
Las variables básicas ahora son X1=1/4 y X2=1/2 (que cumplen las condiciones de no negatividad). Adicionalmente el costo reducido de las variables no básicas también es mayor o igual a cero, por tanto estamos frente a la solución óptima del problema.
Se puede reconocer adicionalmente que el valor óptimo es V(P)=100 que se obtendría al evaluar la solución óptima del problema en la función objetivo, sin embargo, en el procedimiento dicho valor se obtiene con signo cambiado.
El ejemplo anterior nos permitió apreciar cómo a través del Método Simplex Dual se puede abordar la resolución de un modelo de Programación Lineal que luego de ser llevado a la forma estándar no provee una solución básica factible inicial.
Cabe destacar que el Método Simplex Dual que no es la única alternativa algorítmica a la cual podemos recurrir para resolver el problema propuesto. Por ejemplo, podríamos haber alcanzado idénticos resultados aplicando el Método Simplex de 2 Fases con algo más de trabajo.
Alternativamente podríamos definir el modelo dual al problema propuesto y resolverlo por el Método Simplex para posteriormente utilizar las condiciones del Teorema de Holguras Complementarias.
En resumen ante un modelo de optimización contamos con varias alternativas de resolución y es deber de quien resuelve evaluar los distintos caminos en términos de su complejidad y representación.
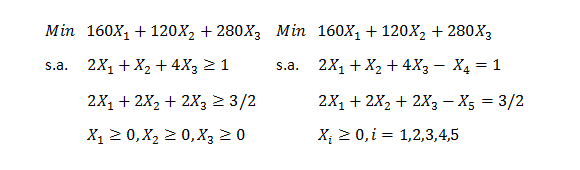
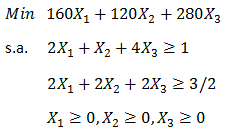
¿Y cuál seria el resultado de X3?
@Hugo. En el óptimo X3 es cero al ser una variable no básica.