método esquina noroeste Archivos - Gestión de Operaciones

Método del Costo Mínimo (Algoritmo de Transporte en Programación Lineal)

El Método del Costo Mínimo determina una mejor solución básica factible inicial que el Método de la Esquina Noroeste debido a que se concentra en las rutas menos costosas.

De esta forma el Método del Costo Mínimo se inicia asignando lo máximo posible a la celda que tenga el mínimo costo unitario (en caso de empates, éstos se rompen de forma arbitraria). A continuación, la fila o columna ya satisfechos de tacha, y las cantidades de oferta y demanda se ajustan en consecuencia. Si se satisfacen de forma simultanea una fila y una columna, sólo se tacha uno de los dos (de forma idéntica que el Método de la Esquina Noroeste). Luego se busca la celda no tachada con el costo unitario mínimo y se repite el proceso hasta que queda sin tachar exactamente una fila o una columna.

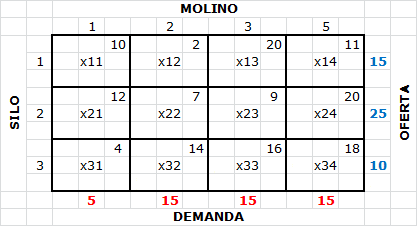
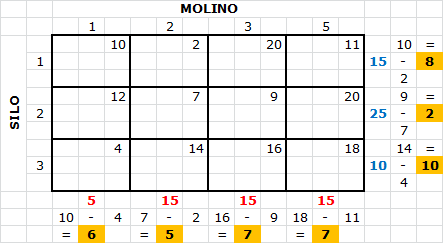
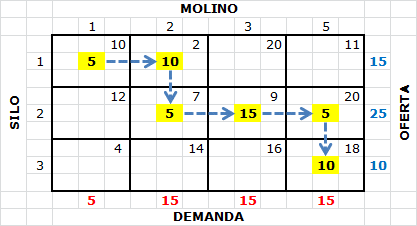
Consideremos nuevamente el Problema de Transporte donde se desea satisfacer la demanda de 4 molinos a través de los envíos de 3 silos, donde los valores en la esquina superior derecha de cada cuadro $c_{ij}$ representan los costos unitarios de transporte desde el silo i al molino j.

Fe de Erratas: En la imagen dice Molino 1, 2, 3 y 5 (columnas). Debería decir: Molino 1, 2, 3 y 4.

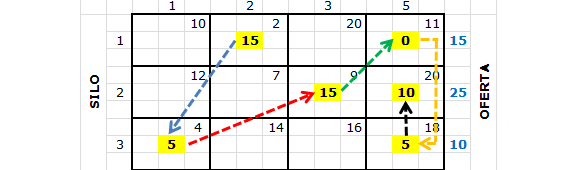
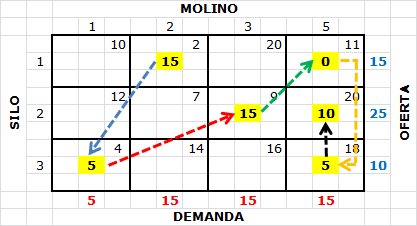
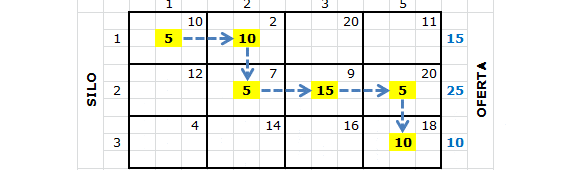
La aplicación del Método de Costo Mínimo al problema de transporte anterior da origen a la siguiente solución factible de inicio:

Los pasos aplicados para llegar a dichos resultados se resumen a continuación:

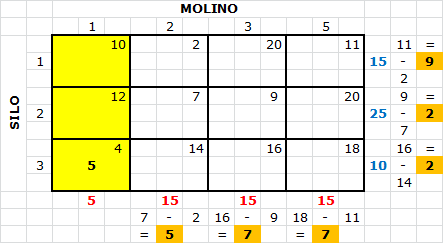
La celda $x_{12}$ tiene el menor costo unitario, por tanto se asigna lo máximo posible (15 unidades correspondiente a la oferta del silo 1). Con $x_{12}=15$ se satisface tanto la demanda del molino 2 como la oferta del silo 1. Se tacha de forma arbitraria la columna 2.
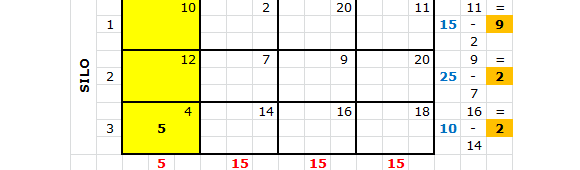
Ahora la celda $x_{31}$ tiene el mínimo costo unitario sin tachar. Se asigna $x_{31}=5$ y se tacha la columna 1 porque quedó satisfecha (lo cual deja una capacidad remanente del silo 3 de 5 unidades).
Al continuar de este modo, se asignan en forma sucesiva 15 unidades a la celda $x_{23}$ , 0 unidades a la celda $x_{14}$ (la capacidad del silo 1 ya fue asignada), 5 unidades a la celda $x_{34}$ y 10 unidades a la celda $x_{24}$ .

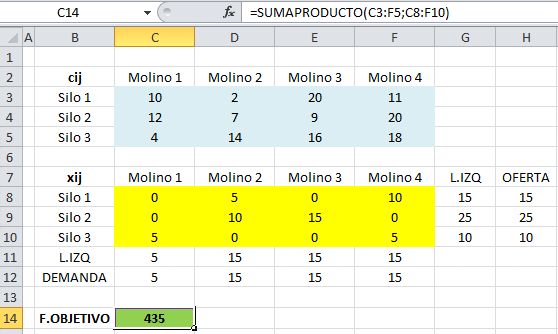
La solución básica factible de inicio resultante con 6 variables básicas es: $x_{12}=15, x_{14}=0, x_{23}=15, x_{24}=10, x_{31}=5, x_{34}=5$ la cual reporta un valor en la función objetivo (costo) de Z=15(2)+0(11)+15(9)+10(20)+5(4)+5(18)=$475 que efectivamente es una mejor solución inicial que la obtenida por el Método de la Esquina Noroeste (que provee un valor de $520 al ser evaluado en la función objetivo) pero por cierto no es la solución óptima según se aprecia en la siguiente imagen que resume la implementación computacional del problema en Solver.

Método de Aproximación de Vogel (Algoritmo de Transporte en Programación Lineal)

El Método de Aproximación de Vogel es una versión mejorada del Método del Costo Mínimo y el Método de la Esquina Noroeste que en general produce mejores soluciones básicas factibles de inicio, entendiendo por ello a soluciones básicas factibles que reportan un menor valor en la función objetivo (de minimización) de un Problema de Transporte balanceado (suma de la oferta = suma de la demanda).

Los pasos que requiere la aplicación del Método de Aproximación de Vogel son los siguientes:

Paso 1: Determinar para cada fila (columna) una medida de penalización restando el elemento de costo unitario mínimo en la fila (columna) del elemento con costo unitario siguiente al mínimo de la misma fila (columna).

Paso 2: Identificar la fila o columna con la mayor penalización. Romper los empates (de existir) de forma arbitraria. Asignar todo lo posible a la variable que tenga el mínimo costo unitario de la fila o columna seleccionada. Ajusta la oferta y la demanda y tachar la fila o la columna ya satisfecha. Si se satisfacen una fila y una columna en forma simultánea, sólo se tacha uno de los dos y al que queda se le asigna oferta o demanda cero.

Paso 3:

Si queda sin tachar exactamente una fila o columna con cero oferta o demanda, detenerse.
Si queda sin tachar una fila (columna) con oferta (demanda) positiva, determinar las variables básicas en la fila (columna) con el Método del Costo Mínimo. Detenerse.
Si todas las filas y columnas que no se tacharon tienen cero oferta y demanda (restante), determinar las variables básicas cero por el Método del Costo Mínimo. Detenerse.
En cualquier otro caso, seguir en el Paso 1.

Ejemplo Método de Aproximación de Vogel

Consideremos nuevamente un problema de transporte balanceado que tiene 3 fuentes de oferta (silos) y 4 fuentes de demanda (molinos). Los valores numéricos en la esquina superior derecha de cada cuadro, en adelante $c_{ij}$ representan el costo unitario de transporte desde el silo i al molino j. Por ejemplo $c_{11}=10$ es el costo unitario de transporte desde el silo 1 al molino 1.

Según lo descrito anteriormente el primer paso consiste en calcular el factor de penalización para cada fila y columna de la tabla que representa el problema de transporte anterior. Por ejemplo, en la fila 1 el mínimo costo es $2 y y el costo unitario siguiente al mínimo es $10. En consecuencia la penalización de dicha fila es $8 ($10-$2). Se replica el mismo cálculo para cada fila y columna de la tabla lo cual es trivial y reporta los siguientes resultados (se han marcado las penalizaciones de las respectivas filas y columnas con color naranjo para mayor claridad):

Como la fila 3 tiene la máxima penalización ($10) y la celda correspondiente a $x_{31}$ tiene el costo unitario mínimo de esa fila, se asigna 5 unidades a $x_{31}$ (más no es necesario aún cuando la capacidad del silo 3 lo permite dado que la demanda del molino 1 es de sólo 5 unidades). Con esto la columna 1 se debe tachar (lo hemos marcado con color amarillo) y se procede a calcular las nuevas penalizaciones como se aprecia a continuación:

Ahora la penalización máxima es $9 ($11-$2) lo cual se alcanza en la fila 1. En consecuencia se asigna la máxima cantidad posible a la variable $x_{12}$ , con lo que se obtiene $x_{12}=15$ , y al mismo tiempo se satisfacen tanto la fila 1 como la columna 2. En forma arbitraria se tacha la columna 2 y se ajusta a cero la oferta en la fila 1.

Al continuar de la misma forma, ahora la fila 2 es la que produce la máxima penalización correspondiente a $11 ($20-$9), por tanto se asigna $x_{23}=15$ , con lo que se tacha la columna 3 y quedan 10 unidades en la fila 2. Sólo queda la columna 4 y tiene 15 unidades de oferta positiva. Al aplicar el Método del Costo Mínimo a esa columna, se asigna de forma sucesiva $x_{14}=0, x_{34}=5, x_{24}=10$ (se recomienda verificar dichos resultados). Notar adicionalmente que hay otras soluciones posibles que dependen de cómo se rompen los empates.

El valor de la función objetivo asociado a esta solución factible inicial es Z=15(2)+0(11)+15(9)+10(20)+5(4)+5(18)=$475 que es similar a lo alcanzado por el Método del Costo Mínimo, no obstante, en general el Método de Aproximación de Vogel reporta mejor solución de inicio.

Método de la Esquina Noroeste (Algoritmo de Transporte en Programación Lineal)

El Método de la Esquina Noroeste (o esquina superior izquierda) es una heurística que se aplica a una estructura especial de problemas de Programación Lineal llamada Modelo de Transporte, la cual permite asegurar que exista una solución básica factible inicial (no artificial). Otros métodos para la obtención de una solución básica de inicio son el Método de Costo Mínimo y Método de Aproximación de Vogel. En general, el Método de Vogel produce la mejor solución básica de inicio y el de la Esquina Noroeste la peor, sin embargo, el Método de la Esquina Noroeste implica el mínimo de cálculos.

El Método de la Esquina Noroeste comienza en la celda (ruta) correspondiente a la esquina noroeste, o superior izquierda, de la tabla (variable $x_{11}$ ). A continuación una descripción de los pasos:

Paso 1: Asignar todo lo posible a la celda seleccionada y ajustar las cantidades asociadas de oferta y demanda restando la cantidad asignada.

Paso 2: Salir de la fila o la columna cuando se alcance oferta o demanda cero, y tacharlo, para indicar que no se pueden hacer más asignaciones a esa fila o columna. Si una fila y una columna dan cero al mismo tiempo, tachar sólo uno (la fila o columna) y dejar una oferta (demanda) cero en la fila (columna) que no se tachó.

Paso 3: Si queda exactamente una fila o columna sin tachar, detenerse. En caso contrario, avanzar a la celda de la derecha si se acaba de tachar una columna, o a la de abajo si se tachó un reglón. Seguir con el Paso 1.

Método de la Esquina Noroeste

Para ilustrar la aplicación del Método de la Esquina Noroeste consideremos el siguiente problema balanceado de transporte que considera 3 silos productos (oferta) que satisfacen las necesidades de 4 molinos (demanda). El algoritmo de transporte se basa en la hipótesis que el modelo está balanceado, es decir, que la demanda total es igual a la oferta total (si el modelo no está balanceado siempre se podrá aumentar con una fuente ficticia o un destino ficticio para restaurar el equilibrio o balance).

Los costos unitarios de transporte desde el silo i al molino j $c_{ij}$ se representan en la esquina superior derecha de cada cuadro. Por ejemplo el costo unitario de enviar una unidad de producto desde el silo 1 al molino 1 es de $10. Adicionalmente los silos 1, 2 y 3 tienen capacidad u oferta de 15, 25 y 10 unidades, respectivamente. Por otra parte los molinos 1, 2, 3 y 4 tienen requerimientos o demanda de 5, 15, 15 y 15 unidades, respectivamente. El modelo esta balanceado (suma oferta = suma demanda = 50 unidades).

Al aplicar el Método de la Esquina Noroeste al ejemplo anterior se obtienen los siguientes resultados. Las flechas indican el orden en el que se generan las cantidades asignadas:

La cantidad asignada a la celda $x_{11}$ son 5 unidades, dado que si bien el silo 1 tiene capacidad de 15 unidades, el molino 1 sólo necesita (demanda) 5 unidades (no se realizan más asignaciones a la columna 1 correspondiente al molino 1).
A continuación nos movemos a la derecha y asignamos lo máximo posible (10 unidades remanentes) a la celda $x_{12}$ (con lo cual se completa la capacidad del silo 1 y en consecuencia no es posible seguir realizando asignaciones en la fila 1).
Luego asignamos 5 unidades a la celda $x_{22}$ lo cual es por cierto menor que la capacidad del silo 2 pero lo suficiente para satisfacer los requerimientos del molino 2 (ahora no es posible generar asignaciones adicionales a la columna 2).
Nos movemos a la derecha y se asignan 15 unidades del silo 2 al molino 3 ( $x_{23}=15$ ) lo que cubre inmediatamente los requerimientos del molino 3 (no es necesario asignar más en la columna 3).
Nuevamente nos movemos a la derecha y asignamos lo máximo posible (5 unidades que es la capacidad remanente del silo 2, es decir, $x_{24}=5$ ) con lo cual el silo 2 opera a máxima capacidad (ahora ya no es posible nuevas asignaciones en la fila 2).
Finalmente se asignan 10 unidades del silo 3 al molino 4 ( $x_{34}=10$ ) cubriendo la demanda de dicho molino (y la capacidad del correspondiente silo).

En consecuencia la solución básica factible inicial es: $x_{11}=5, x_{12}=10, x_{22}=5, x_{23}=15, x_{24}=5, x_{34}=10$ que reporta un costo del programa (valor en la función objetivo) de: Z=5(10)+10(2)+5(7)+15*(9)+5(20)+10*(18)=$520. Notar que si se implementa computacionalmente el problema anterior haciendo uso de Solver de Excel y utilizando como motor de resolución Simplex_LP se alcanza la siguiente solución óptima (celdas amarillas) con costo mínimo (valor óptimo) de $435.