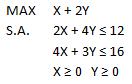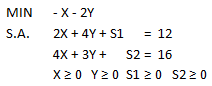Una de las posibilidades a las que nos podemos enfrentar cuando resolvemos un modelo de Programación Lineal a través del Método Simplex es el caso de múltiples o infinitas soluciones óptimas.
Esto significa que existe un tramo de soluciones factibles que reportan idéntico valor para la función objetivo y que no es posible mejorar.
En este contexto si luego de aplicar las iteraciones que resulten necesarias por el Método Simplex a un modelo de Programación Lineal (tabla óptima o tableau óptimo) se verifica que una variable no básica óptima tiene costo reducido igual a cero, esto permitirá afirmar que estamos ante el caso de infinitas soluciones.
Ejemplo Infinitas Soluciones Óptimas Método Simplex
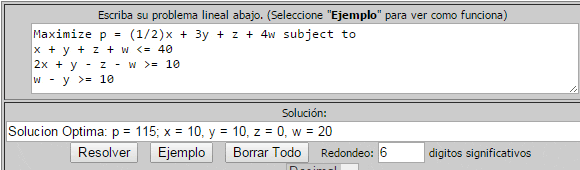
Consideremos el siguiente modelo de Programación Lineal:
Llevamos el modelo a su forma estándar para proceder con la aplicación del Método Simplex, con S1 y S2 como variables de holgura de la restricción 1 y 2, respectivamente.
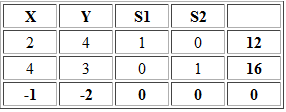
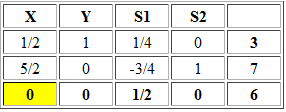
La tabla inicial con S1 y S2 como variables básicas iniciales es:
Y entra a la base. Luego para determinar la variable que deja la base utilizamos el criterio del mínimo cuociente: Min {12/4 ; 16/3} = 3 ==> S1 deja la base. Con esta información actualizamos la tabla realizando operaciones fila:
Luego de una iteración encontramos la solución óptima, donde Y y S2 son variables básicas. La solución básica factible óptima es X=0 Y=3 S1=0 S2=7. El valor óptimo es V(P)=6.
Notar que X (variable no básica) tiene costo reducido igual a cero lo que determina la existencia de múltiples o infinitas soluciones óptimas, de modo que la solución actual es uno de los vértices óptimos.
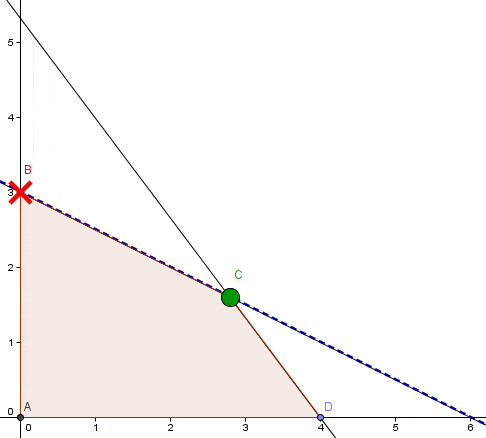
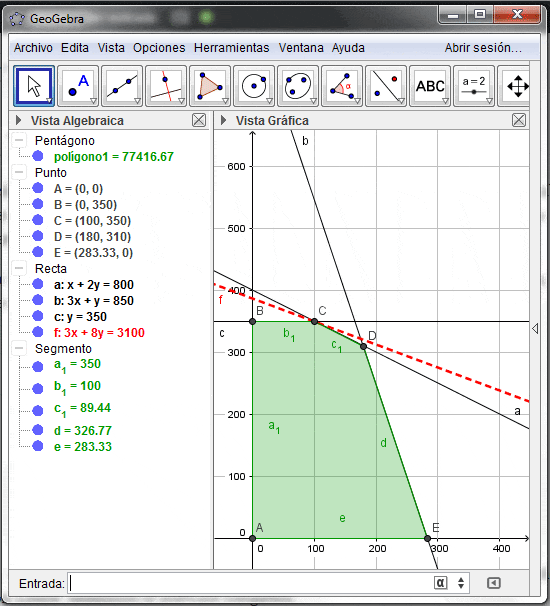
El siguiente diagrama muestra la Resolución Gráfica del problema con el software Geogebra donde la solución óptima que hemos encontrado en la aplicación del Método Simplex corresponde al vértice B.
Notar que la línea punteada de color azul corresponde a una curva de nivel de la función objetivo que tiene la misma pendiente que la restricción 1 (pendiente -1/2).
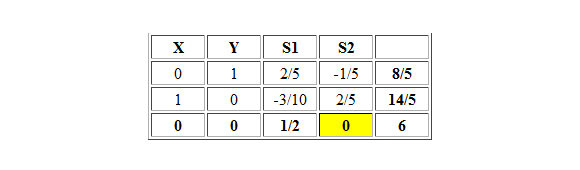
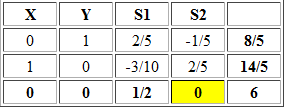
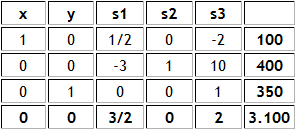
¿Cómo podemos obtener el vértice C que es solución óptima a través del Método Simplex? Una alternativa sería forzando la entrada a la base de la variable X en la tabla óptima. Luego calculamos cuál de las actuales variables básicas deja la base según el criterio del mínimo cuociente: Min {3/1/2 ; 7/5/2} = 14/5 ==> S2 deja la base. Actualizando la tabla obtenemos:
La nueva solución óptima (con idéntico valor óptimo) es X=14/5 Y=8/5 S1=0 S2=0, que corresponde al vértice C en el gráfico anterior. Ahora la variable no básica S2 tiene costo reducido igual a cero en la tabla óptima que señala el caso de múltiples soluciones óptimas (en este ejemplo el tramo BC).